一道模考题的解法剖析及教学反思



一道模考题的解法剖析及教学反思

浙江省绍兴市柯桥区越琦中学(312050)朱海英浙江省绍兴市高级中学(312000)阮伟强

1问题的提出

近日，我校高三年级的一次模拟考试中，有这样一道考题：

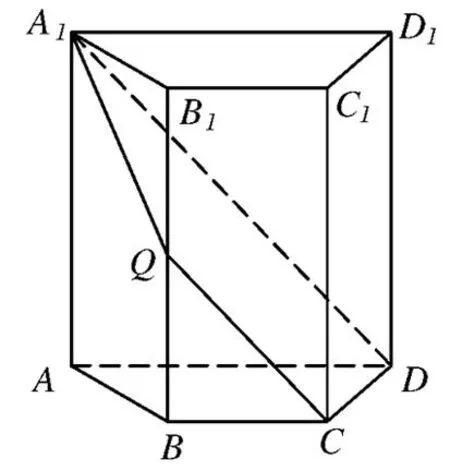
图1

如图1，四棱柱ABCD-A1B1C1D1中，AA1⊥底面ABCD.四边形ABCD是梯形，AD∥BC，且AD=2BC.过A1,C,D三点的平面记为α，BB1与α的交点为Q.

(Ⅰ)证明：Q为BB1的中点；

(Ⅱ)若AA1=4，CD=2，梯形ABCD的面积为6，求平面α与底面ABCD所成二面角的大小.

本题以学生熟悉的棱柱为载体，图形规则、简洁，利于识图、想图.问题设置也平和、常见，所用解法均为立体几何的重要方法，体现了“源于教材、高于教材”的命题原则.然而，阅卷发现：学生的得分情况却不容乐观，“会而不对、对而不全”的现象较为普遍，更令人担忧的是：答卷中较多出现说理不清、逻辑混乱、想当然等现象.因此，有必要在试题解法剖析的基础上，就目前(新课程背景下)的立体几何教学进行客观、冷静的反思.

2解题分析

2.1　第(Ⅰ)问的解题分析

该问入口较宽，方法多样，但综合法明显优于坐标法.

评析：此法的最大优势是不用添加任何辅助线，关键是证出直线QC和A1D平行.学生虽直观能看出这一点，但不知道如何推理.表现在：或是干脆不证；或是面面平行判定和性质定理运用时，条件没有全部列举出来，逻辑不够严密.

评析：此法因推理过程较长，学生“跳步”作答的现象较严重，既不符合逻辑推理的规范，也给评分造成了较大的障碍.

图2

评析：此法的关键是证出直线AB,CD,A1Q共点，学生大都默认了这一点，想不到也不会用公理3加以证明，导致推理存在很大的缺陷.

图3

证法4：如图3，延长线段CB至点F，使得FB=CB.过点F作FF1∥AA1，且FF1=AA1，连结AF,A1F1，B1F1，CF1，则底面AFCD为平行四边形，平行六面体AFCD-A1F1C1D1为直四棱柱，且平面A1F1CD就是平面α，点Q=CF1∩BB1，所以Q为BB1的中点.

评析：此法的关键是“补形”后，需说明一点：平面A1F1CD就是平面α，学生基本上避而不谈.另外，作法描述不清也较为普遍.

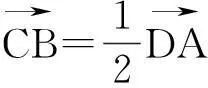
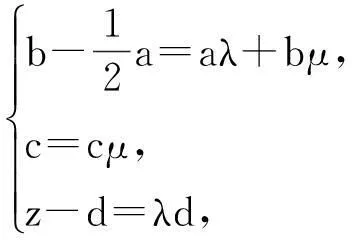
评析：很少有学生选择用坐标法来证，这个决定无疑是正确的.个别学生仍选择坐标法，但草草建系后便难以为继，原因有二：一是因引进字母太多，心理压力大，觉得运算会很麻烦，就选择放弃；二是四点共面的几何条件不能转译为向量应满足的关系(平常用得不多).

评析：此法的“向量味”更浓，突出的是基底思想和“回路”算法的运用，较之坐标法有一定的优势.但无学生选择，这恐怕与实际教学更偏重于坐标法有关，值得我们思考.

2.2　第(Ⅱ)问的解题分析

从所求二面角的空间位置看，作出其平面角还是常见、容易的.因此，本小题的求解也是综合法优于坐标法.

评析：令人惊讶的是，不少学生虽得出了正确答案，但推理存在很大的漏洞：就是想当然地认为∠ADC是直角，进而得∠ADA1是所求二面角的平面角，接下来，可以说凭口算就能得到答案.这无疑暴露了一点：学生的空间想象能力明显不足，导致无法正确认识图形.事实上，ΔACD只有一边及高定，其形状并不定(∠ADC可取任意一个角)，只是所求二面角的大小只与高有关，故能凑巧得到答案，但犯下的逻辑错误是用特殊代替一般的推证.

评析：此法的关键是借参数θ表示相关点的坐标，后续向量的坐标运算就变得简单.学生存在的问题是：习惯于直接设点的坐标，导致参数有3个，接下来，建立参数的关系式，感觉面积条件很别扭，不知如何用.另外，也有部分学生将∠ADC视作直角来建系，犯了上面提及的相同错误.

3教学反思

从解法的剖析发现，本题的难度并不大.那么，为什么学生会暴露出这么多的问题？原因恐怕在：学生对立体几何的知识、方法、思想的认识、理解和掌握远没有达到本质的程度，解题模式化现象严重，对稍有改变的问题设置适应性差，逻辑推理能力下降更是不争的事实.因此，十分有必要就目前的立体几何教学做以下反思.

3.1　加强推理能力的训练

新课程中的立体几何的结构体系有了重大改革，目的是适当减轻几何论证的难度，降低立体几何学习入门的门槛，提高学生学习立体几何的兴趣.但如果因这个变化，就认为《课标》降低了对推理论证的要求是不够全面的.只是与旧教材相比，《课标》对推理论证的要求不是一步到位，而是分阶段、分层次、多角度的达到.另外，在立体几何初步中，由“直观感知、操作确认”来获取相关的判定定理，虽不要求证明，但也不能仅停留在观察、实验操作等层面上，其间应加大“说理”的成分，让学生更信服.若有学生表现出想“证明”的热情与欲望，教师更应保护与支持，并进行必要的说明与引导.面对直观容易判断的结论，能要求学生证明一下，教师再着重强调，适当示范，通过推理案例来强化推理语言的书写，逐步使学生养成缜密的推理习惯，实现“脑能呈现、口能表述、笔能书写”的效果.

3.2　“综合几何”的地位不能削弱

的确，向量兼具代数与几何的双重身份，通常可以省略构图的繁琐，在解决立体几何问题时具有独特的优势.然而，凡事都有两面性.向量法在增加运算的同时，也大幅减少了几何推理，久而久之，学生的眼中只有计算求解，没有逻辑证明.教材中的定义、公理、定理、推论等立体几何知识，只能成为学生脑海中的模糊记忆，说不清楚、讲不明白，更是用不顺手.因此，立体几何教学应以综合几何为基础，与向量几何相互配合，“两条腿走路”，既能真正落实几何教学的主要目标—培养学生的空间想象能力和逻辑推理能力，又能使一些繁难的几何问题得到有效解决.

3.3　空间想象能力的培养是核心

立体几何复习的一般顺序是：先立体几何初步的内容，再是向量方法.但空间想象能力的培养不能割裂，应贯穿始终.具体可突出：(1)充分利用模型.要始终如一地发挥模型在立体几何学习中的作用，培养学生丰富的立体感，让学生感受空间图形是各种实物的进一步抽象，增强空间图形真实感，为空间想象能力的提升奠定基础.(2)加强对三视图的教学.要求学生：首先能依据三视图讲得出几何体的大致结构、名称等；其次，一定要画出相应的直观图(实际教学中常被疏忽)；第三，依据直观图，将探知的结果与三视图对比，以确保准确无误.(3)在向量法的运用中，无论是建系，还是向量结论翻译成几何结果，一定要让学生不断回到图形，进行验证与识别，做到先识图再算，边算边识图、想图.