高校论文答辩排班模型与应用

方 刚， 徐 哲， 顾 坤

(北京航空航天大学 经济管理学院，北京 100191)

高校论文答辩排班模型与应用

方 刚， 徐 哲， 顾 坤

(北京航空航天大学 经济管理学院，北京 100191)

论文答辩排班是高校教务管理中的重要任务，答辩排班结果的质量直接影响评审的公平性。详细分析高校论文答辩排班问题的特性和情景，保证评审的公平性，考虑评审人在不同研究方向上擅长程度的差异、评审人能参加答辩的时间安排要求、评审人与答辩人可能存在的师生关系、评审人评审工作量的限制、每个答辩组中答辩人数和评审人数的限制，等等因素，建立答辩分组和组内评审指派的两阶段非线性整数规划人员排班模型，对答辩排班问题的复杂性进行分析，基于lingo软件中的分支定界算法对问题进行求解，通过实例验证了模型的可靠性和求解结果的合理性，较好地解决了高校答辩排班问题。

教务管理； 答辩排班； 人员排班； 非线性规划； 整数规划

答辩排班是高校教务管理中的重要工作。近年来，随着高校招生规模的扩大，毕业生答辩排班工作变得复杂和困难，传统的手工排班方式难以解决大规模答辩排班问题，极大影响了答辩工作的顺利开展。

人员排班问题是NP-hard问题[1]，已有相关文献发表了诸多研究成果。文献[2]将人员排班问题分为：一般的人员排班问题，大众运输的人员排班问题，航空公司的人员排班问题。其中，一般的人员排班问题是一种小型的人员排班问题，如护士排班问题[3-5]和作业人员排班问题[6]等；而大众运输的人员排班问题[7]和航空人员的排班问题则属于大型的排班问题，这类排班问题往往计算复杂度高，排班过程复杂繁琐。护士排班问题是一类经典的人员排班问题，这类人员排班问题要考虑的特殊因素是护士需要在不同的班次之间进行轮换，这不仅扰乱了护士正常的作息时间，而且很可能影响其正常的家庭生活和对其自身的健康造成影响[8]。因此，如何通过合理安排护士的排班班次，使得她们既能完成应有的工作，又能得到充分的休息，并能履行好其家庭角色是研究护士排班问题的重点[9]。目前国内外对护士排班问题[10]的研究分为以下几种。1)基于人员特性和排班班次的护士排班问题的研究，这类问题往往需要考虑一些人员特性(诸如人员的技能差异、人员间的配合默契程度等)和排班班次(如三班制、组别等)等因素。如文献[11]通过调整排班班次的方法，一定程度上解决了护士班次频繁变化的问题。2)基于约束的护士排班问题，主要是从护士排班问题的约束条件入手，将其约束条件分为硬性约束[12-16]和非硬性约束[17-21]，如文献[22]针对护士排班问题建立了一个完整的带有劳动法规约束和考虑护士级别差异的问题模型。文献[23]将护士的工作满意度以及个人偏好等因素条件考虑进护士排班问题中，一定程度上解决了护士排班问题中护士满意度以及个性化要求等问题。3)基于护士排班问题求解方法的研究，有数学规划方法、智能算法、启发式方法、元启发式方法等[24-26]。

高校答辩排班问题和护士排班问题具有一定的相似性，目前这类排班问题相关的研究文献很少。文献[27]在答辩排班问题中利用时间位图算法求解基于各种资源(评审人、答辩时间、答辩场地等)冲突的答辩排班问题，并在此基础上研发了一个研究生毕业答辩信息系统；文献[28]综合考虑师生关系约束、答辩评委的组成和时间安排约束等因素，建立了一个考虑答辩评委的工作强度以及评审时间连续性的双目标规划模型。以上文献一定程度上研究了答辩排班分组的问题，但对于答辩排班问题中评审的“公平性”原则未有涉及。本文认为答辩排班问题需要考虑评审人在不同研究方向上擅长程度的差异、评审人与答辩人之间可能存在的师生关系、答辩周期短和时间紧凑等因素，满足评审人对答辩时间安排的特殊要求，为了保证答辩质量还要规定评审人的劳动强度上限，等等，合理优化答辩人和评审人分组和评审指派任务，实现答辩排班问题中评审的“公平性”。

本文在现有的人员排班问题研究的基础上，充分考虑答辩排班问题的特性,即排班工作的任务、内容、技能差异、师生关系、人员的劳动强度与时间等因素，分别以评审人和答辩人在研究方向上的“最大匹配度”以及“评审的公平性”为优化目标，建立一个两阶段的非线性整数规划模型(分组阶段以及组内指派阶段)，并基于lingo软件中的分支定界算法对小规模答辩排班的模型进行了求解，最后通过实际算例验证了本文建立的答辩排班模型的可靠性和求解结果的合理性。

1 问题描述

高校答辩排班问题中，每个答辩人的论文研究方向不尽相同，评审人对各个研究方向的熟悉程度也并非相同。为了提高答辩过程和结果的公正性和有效性，在进行答辩排班时需要根据答辩人的论文研究方向进行合理分组，并指派对此研究方向熟悉的评审人对其论文进行评审。因此，基于某一研究方向，尽可能将具有相同或者相似研究方向的答辩人，以及对此研究方向尽可能熟悉的评审人分在一组。除此之外，还要考虑到评审人在时间安排上的特殊要求，以及考虑到答辩人与评审人之间可能存在的师生关系而不能安排在同一个答辩组，等等。具体而言，答辩排班问题必须满足以下要求：

1)答辩时间为教学规定的日期；

2)答辩场所为教学规定的地点；

3)每个答辩组的评审人数在一定的范围内；

4)每位评审人参加的答辩组数在一定的范围内；

5)每个答辩组参加答辩的人数在一定的范围内；

6)评审人参加答辩的时间与评审人要求的时间不相冲突；

7)评审人应该对本组答辩人的研究方向尽可能熟悉；

8)每个答辩组中评审人与答辩人之间不存在师生关系；

9)每个评审人在一个时间段内只能被安排在一个地点参加答辩工作；

10)每个答辩人有且只能参加某个答辩组(某个地点的某个时间段)的一场答辩。

2 建模分析

2.1 变量与参数说明

1)决策变量。

(1)xltp为0-1变量，xltp=1表示评审人l被安排在第t时间段第p场地的答辩小组，反之为0；

(2)ystp为0-1变量，ystp=1表示答辩人s被安排在第t时间段第p场地的答辩小组，否则为0。

2)参数。

(1)blt为0-1变量，blt=1表示第l个评审人参加第t时间段的答辩，反之则为0；

(2)clm为等级变量，取值为0,1,2,3,4,5，数值越大表示评审人l对研究方向m越擅长；

(3)asl为0-1变量，asl=1表示评审人l与答辩人s之间存在师生关系，反之则为0；

(4) ∂1、∂2分别为每个答辩小组评审人数的下限和上限;

(5)v为一个排班周期内，每位评审人参加的答辩组数的上限；

(6)β1,β2分别表示每个答辩小组答辩人数的下限和上限;

(7)ms为答辩人s的论文研究方向m的编号；

(8)ktp为0-1变量，ktp=1表示第t时间段第p个答辩地点可以安排答辩，反之则为0。

2.2 建立模型

答辩排班模型的优化目标是在一个答辩周期内，满足一系列约束条件的限制，使得评审人和答辩人在研究方向上实现最大匹配，由此保证答辩的公正性和公平性。本文将答辩排班过程分为2个阶段：答辩分组阶段和组内评审指派阶段。答辩分组阶段的任务是将所有的答辩人和所有的评审人分组，即综合各组(某个地点和某个时间段)的评审人和答辩人在研究方向上实现最大匹配。组内指派阶段的任务是在已分组的情况下，在组内依据研究方向匹配原则为每个答辩人指派若干名论文评审人。

2.2.1 建立答辩分组模型

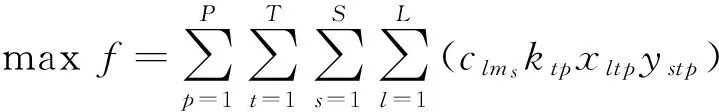
(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

xltp∈{0,1},ystp∈{0,1}。

(10)

式(1)为答辩分组阶段的优化目标，即综合所有答辩人被指派的论文评审人对其论文研究方向的熟悉程度赋值总和最大；

约束(2)为每组评审人数的上下限；

约束(3)为每位评审人参加的答辩组数的上限；

约束(4)为每组答辩人数的上下限；

约束(5)为评审人能够在指派的时间参加评审与答辩，该时间与评审人的时间要求不冲突；

约束(6)为指派的评审人要擅长答辩人论文研究方向，即擅长程度的取值不能为0；

约束(7)为在同一答辩小组，评审人与答辩人不能存在师生关系；

约束(8)为每个评审人一个时间段只能被安排在一个地点参加答辩工作；

约束(9)为每个答辩人必须有且只能参加一个答辩组(某个时间的某个地点)的答辩；

约束(10)为评审人和答辩人的决策变量。

2.2.2 建立组内评审指派模型

定义Li′为第i组评审人的集合，Si′为第i组答辩人的集合，wi,ni分别为第i组评审人和答辩人的数量，zls=1表示评审人l被指派评审答辩人s的论文，zls=0表示不存在评审关系。组内指派阶段的任务是在第一阶段答辩排班分组的基础上，在各组内依据研究方向匹配原则为每个答辩人指派若干名论文评审人。

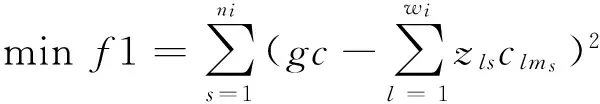
(11)

(12)

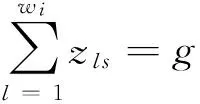
(13)

zls∈{0,1}。

(14)

式(11)为组内评审指派阶段的优化目标，表示在组内为每个答辩人指派若干名评审人，要求最大化评审的公平性，即组内为所有答辩人指派的评审人在研究方向的擅长值总和与最大擅长值总和之间的偏差最小。c=5为常数，表示评审人和答辩人在研究方向的最大匹配值。若某个答辩组共有8名答辩人，为每位答辩人指派2位评审人，则针对每个答辩人而言，最大擅长值总和为2×5=10，则该组的最大擅长值总和为10×8=80。

约束(12)表示每名评审人至少评审1名答辩人的论文，至多评阅h名；

约束(13)表示必须为每个答辩人指派g名评审人；

约束(14)为答辩人与评审人评审关系的决策变量。

2.3 答辩排班结果的评价指标

为了评价计算结果的合理性和可靠性，本文分别提出了2个阶段计算结果的评价指标。在答辩分组阶段采用研究方向匹配度表示组内擅长答辩人研究方向的评审人数占该组总的评审人数的比例，该比例越大说明分组结果越合理；在组内评审指派阶段采用评审匹配度更精准地评价评审指派的合理性和有效性，用组内为所有答辩人指派的评审人在答辩人研究方向上的擅长程度值的总和与当取最大擅长值(取值为5)总和的比值表示，该比值越大说明评审过程和结果越公平合理。

2.3.1 研究方向匹配度

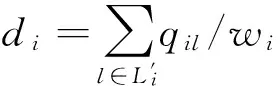
(15)

式中，i为答辩小组的编号；qil定义第i组第l个评审人对组内答辩人研究方向的擅长关系取值，假设Ai为第i组答辩人研究方向的集合，Bi为第i组评审人研究方向的集合，则当且仅当qil∈Ai且qil∈Bi时，有qil=1，表示该评审人擅长组内某个答辩人的研究方向，否则，qil=0。

2.3.2 评审匹配度

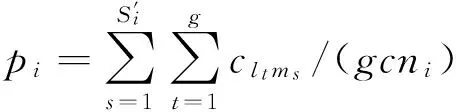
(16)

式中，t为评审人的编号；cltms为评审人lt对答辩人s的研究方向ms的擅长程度值；g表示为每个答辩人指派的评审人数。

2.4 问题复杂度分析

在所有的人员排班问题中，很少有研究答辩排班问题求解的复杂性的文献。本文试图通过将该答辩排班分组阶段问题降解转化为0-1背包问题，以此来证明该答辩排班问题是NP-hard。

(17)

(18)

(19)

(20)

(21)

x1tp∈{0,1},ystp∈{0,1}。

(22)

上述简化形式是一个0-1背包问题，这表明任何0-1背包问题都可以转换为该答辩排班问题的一个特例，即该答辩排班问题是NP-hard。

3 算例研究

3.1 实例数据

本文的实例数据采集自北京某大学某次硕士答辩数据库，描述了某个答辩周期内有40位答辩人，共涵盖了6个研究方向，有22位评审人可以参加本次评审工作，所有答辩人被安排在2d(4个时间段)内进行答辩，所有答辩被安排在3个场地进行答辩；每个答辩小组的答辩人数限制在8～9人，评审人数限制在6人，在每个答辩组内每个评审人最多可评阅3个答辩人的论文，每个答辩人的论文有且只能由2名评审人进行评阅；考虑到评审人员的精力有限，为保证评审质量，要求在一个答辩周期间，每个评审人最多可以参加3个答辩小组的评审工作。

所有采集的数据列于表1～5，其中：表1为评审人对答辩时间的要求；表2为评审人对研究方向的擅长程度的赋值，要求每位评审人分别给出3个最擅长的研究方向，并按照擅长程度，赋值为1～5，在其余方向均赋值为0；表3为答辩人的研究方向，“1”表示为答辩人的研究方向，否则为“0”；表4为评审人和答辩人的师生关系表，表中共有10对有师生关系的答辩人和评审人；表5为答辩时间和答辩地点关系表，“1”表示某个答辩时间和某个答辩地点可安排答辩，“0”则表示不可安排。

表1 评审人对答辩时间要求表Tab.1 Arrangement of the reviewers’ time

表2 评审人对研究方向的熟悉程度表Tab.2 The extent to which the reviewers are familiar with the research

表3 答辩人研究方向表Tab.3 The research field of the respondents

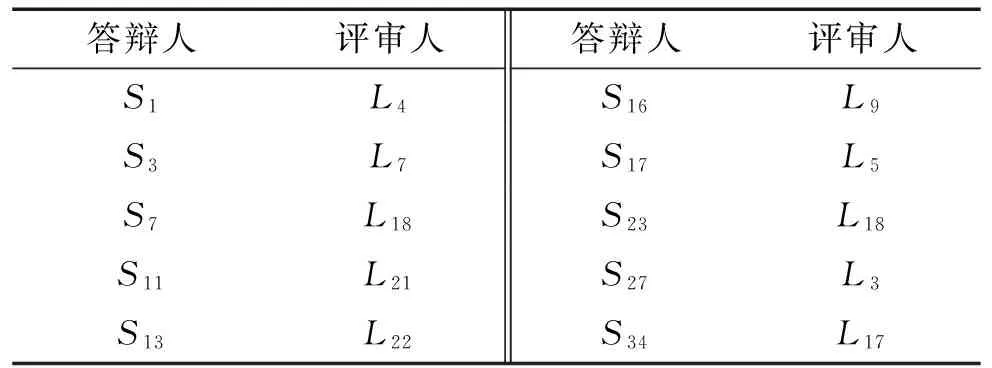
表4 评审人和答辩人的师生关系表Tab.4 Relationships between respondents and reviewers

表5 时间地点关系表Tab.5 Relationship between time and place

3.2 计算结果

本文对答辩排班问题的求解是在win7(CPU AMD A10-7300 Radeon R6,10 Compute Cores 4C+6G 1.90GHz)64位系统下，由lingo软件中的分支定界算法计算得到的。

3.2.1 答辩分组阶段的计算结果

表6是答辩排班分组阶段的计算结果，本次答辩排班共分为5组，表6列出了每组的答辩时间、地点、研究方向、评审人和答辩人的相关信息。

表6 排班分组阶段结果表Tab.6 Results of grouping stage

3.2.2 组内指派阶段的计算结果

答辩排班组内评审指派阶段以“评审的公平性”为目标，在第一阶段答辩分组的基础上，进行组内的人员指派，得到最终的答辩排班结果。表7分别给出了各组的答辩时间、答辩地点、答辩人及其研究方向、为每个答辩人指派的评审人，最后还给出了每个答辩小组答辩排班结果的评价指标值。

3.3.3 计算结果的评价

从表7可以看出答辩排班分组结果合理，研究方向匹配度均为100%，反映了在各个答辩排班分组中，每个评审人至少对组内包含的一个研究方向是擅长的；组内指派结果中各组评审匹配度均在80%以上，其中第4组的答辩排班评审匹配度最高，达到97.5%，该组中答辩人的研究方向与指派的评审人的研究方向匹配程度高，仅有答辩人S34的论文为研究方向5，而指派的2名评审人对该研究方向非最擅长；而第2组的评阅匹配度最低，为82.5%，这是因为该组中有6名答辩人的论文为研究方向3，而为他们指派的2名评审人中至少有1名对该研究方向非最擅长(评审人在各个研究方向上的擅长程度值见表2)。

为了进一步分析各组评审匹配度存在差异的原因，本文绘制了在不同研究方向上不同擅长程度的评审人数分布图(图1)，以及在各个研究方向上答辩人数分布图(图2)。从图1和图2可以看出研究方向1(M1)的答辩人数最多，为10人，且十分擅长该方向的评审人数也最多(D5表示擅长程度值为5)，有8人，所以在满足师生关系以及评审人时间要求等约束条件下，第5组的评审匹配度较高，达到95%；从表7可知，第2组中研究方向3的答辩人数较多(6人)。但从图1和图2可知，十分擅长该方向的评审人数最少，为1人，因而该组的评审匹配度较低，为82.5%。

由以上分析可以看出，本次答辩排班结果满足所有约束条件，该结果能够充分发挥评审人的优势，使评审更加公平、客观和精准，由此可说明本文建立的答辩排班模型能够较好地解决答辩排班问题。

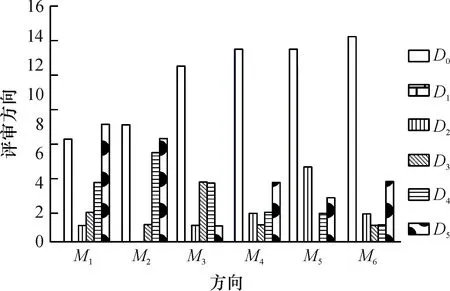
图1 在各个研究方向上不同擅长程度的评审人数分布图Fig.1 Number of reviewers in each research direction

图2 在各个研究方向上答辩人数分布图Fig.2 Number of respondents in each research direction 表7 组内指派结果表Tab.7 Results of assignment stage

组号时间/地点答辩人评审人方向2方向4匹配度值1T1/P1S16L2,L14研究方向匹配度S17L2,L14d1:100%S26L11,L15评审匹配度S27L11,L15p1:90%S28L11,L13S29L7,L15S30L7,L13S31L7,L13方向1方向3方向62T1/P3S3L4,L19研究方向匹配度S19L18,L19d2:100%S20L4,L20评审匹配度S21L18,L22p2:82.5%S22L12,L20S24L4,L20S25L18,L22S36L12,L22方向3方向5方向63T2/P2S23L17,L20研究方向匹配度S32L5,L17d3:100%S33L17,L20评审匹配度S35L8,L20p3:96.25%S37L12,L22S38L8,L12S39L12,L22S40L8,L22方向1方向2方向54T3/P2S7L1,L9研究方向匹配度S11L5,L9d4:100%S12L11,L13评审匹配度S13L11,L13p4:97.5%S14L11,L13S15L5,L14S18L9,L14S34L5,L14方向15T4/P3S1L3,L5研究方向匹配度S2L1,L5d5:100%S4L1,L2评审匹配度S5L3,L11p5:95%S6L2,L21S8L1,L3S9L2,L11S10L5,L21

4 结论

本文针对高校毕业生答辩排班问题，详细分析了问题的特性和情景，建立了答辩分组和组内指派两阶段的非线性整数规划排班模型，并且通过实例验证了模型的可靠性和求解结果的合理性，较好地解决了高校答辩排班工作复杂和准确性差等问题。除此以外，本文还探讨了影响答辩排班问题求解效果的因素，开展了部分相关因素的参数分析，研究结果表明：评审人和答辩人在各个研究方向上人数分布的匹配性、每个答辩组评审人数和答辩人数的取值范围、评审人的时间要求、评审人与答辩人师生关系对的多少，等等，这些因素对排班结果的质量有着重要的影响。由于篇幅所限，本文未列出这部分的研究过程。

由于答辩排班问题属于NP-hard问题，针对大规模的毕业生答辩排班问题，利用分支定界算法求解此问题的时间过长，因而设计一种有效的启发式算法和智能优化算法，既能保证解的质量又能缩短求解的时间将是今后研究的重点。另外，还可以根据实际情况进一步改进答辩排班模型。例如，考虑到评审人的劳动强度，可以增加评审人一天只能参加一个时间段答辩工作的要求，还可以根据实际情况对评审人在所有研究方向的擅长程度赋值，而不仅仅对最擅长的3个研究方向赋值。

[1] YAN S, YANG T H, CHEN Y C. A model and a solution algorithm for airline line maintenance manpower supply planning with multiple aircraft type maintenance certificates[J].Journal of the Chinese Institute of Engineers,2004,27 (5):719-729.

[2]BEASLEY J E, CAO B. A tree search algorithm for the crew scheduling problem[J]. European Journal of Operational Research, 1996, 94(3): 517-526.

[3]WARNER D M, PRAWDA J.A mathematical programming model for scheduling nursing personnel in a hospital[J]. Management Science, 1972, 19(4-part-1): 411-422.

[4]WARNER D M.Scheduling nursing personnel according to nursing preference:a mathematical programming approach[J]. Operations Research, 1976, 24(5): 842-856.

[5]MUSA A A, SAXENA U. Scheduling nurses using goal-programming techniques[J].IIE transactions,1984,16(3):216-221.

[6]BUFFA E S, COSGROVE M J, LUCE B J. An integrated work shift scheduling system[J].Decision Sciences,1976,7(4):620-630.

[7]WREN A, WREN D O. A genetic algorithm for public transport driver scheduling[J].Computers & Operations Research, 1995, 22(1): 101-110.

[8]沈吟东,苏光辉. 带约束的护士排班模型和基于变换规则的优化算法[J].计算机工程与科学,2010,32(7):99-103

SHEN Yindong, SU Guanghui. Models and solutions based on switch rules for nurse scheduling with constraints[J].Computer Engineering & Science, 2010,32(7):99-103

[9]刘晓荣,陈国良,顾仁萍,等.护士排班决策支持系统模型的研究[J].解放军护理杂志,2006,23(2):7-9.

LIU Xiaorong,CHEN Guoliang,GU Renping,et al.A study on nurse scheduling decision support system model[J].Nursing Journal of PLA,2006,23(2):7-9.

[10] VAN DEN BERGH J, BELIЁN J, DE BRUECKER P, et al. Personnel scheduling: a literature review[J]. European Journal of Operational Research, 2013, 226(3): 367-385.

[11]BRUCKER P, BURKE E K, CURTOIS T, et al. A shift sequence based approach for nurse scheduling and a new benchmark dataset[J]. Journal of Heuristics, 2010, 16(4): 559-573.

[12]AICKELIN U, BURKE E K, LI J P. An evolutionary squeaky wheel optimization approach to personnel scheduling[J].IEEE Transactions on Evolutionary Computation, 2009,13(2):433-443.

[13]AVRAMIDIS A N, CHAN W, GENDREAU M, et al. Optimizing daily agent scheduling in a multiskill call center[J].European Journal of Operational Research, 2010, 200(3):822-832.

[14]VALOUXIS C, GOGOS C, GOULAS G, et al. A systematic two phase approach for the nurse rostering problem[J].European Journal of Operational Research, 2012, 219(2):425-433.

[15]AICKELIN U, WHITE P. Building better nurse scheduling algorithms[J].Annals of Operations Research 2004,128:159-177.

[16]AL-YAKOOB S M, SHERALI H D.Mixed-integer programming models for an employee scheduling problem with multiple shifts and work locations[J].Annals of Operations Research, 2007,155(1):119-142.

[17]MORA M, MUSLIU N. Genetic algorithm for rotating workforce scheduling problem[C/OL].(2005-06-13).http://ieeexplore.ieee.org/document/1437685.

[18]MUSLIU N.Combination of local search strategies for rotating workforce scheduling problem[C].International Joint Conference on Artificial Intelligence.Edinburgh:Lawrence Erlbaum Associates LTD, 2005.

[19]NAUDIN E, CHAN P Y C, HIROUX M, et al. Analysis of three mathematical models of the staff rosteringproblem[J].Journal of Scheduling, 2012, 15(1):23-38.

[20]NI H, ABELEDO H.A branch-and-price approach for large-scale employee tour scheduling problems[J].Annals of Operations Research, 2007, 155(1):167-176.

[21]NISSEN V,GÜNTHERM.Staff scheduling with particle swarm optimisation and evolution strategies[M]. Berlin:Springer Berlin Heidelberg,2009.

[22]沈吟东,陈名晖,邓婕.利用矩阵向量化变换求解护士排班问题[C/OL].(2008-07-02).http://www.docin.com/p-596489962.html.

SHEN Y D,CHEN M H,DENG J.Solving nurse scheduling problems aided by vectorization of matrices[C].(2008-07-02).http://www.docin.com/p-596489962.html.

[23]MAENHOUT B,VANHOUCKE M.Analyzing the nursing organizational structure and process from a scheduling perspective[J]. Health Care Management Science, 2013, 16(3): 177-196.

[24]HASEGAWA S,KOSUGI Y.Solving nurse scheduling problem by integer-programming-based local search[C/OL].(2016-10-08).http://ieeexplore.ieee.org/document/4274059.

[25]ISKEN M W,HANCOCK W M.A heuristic approach to nurse scheduling in hospital units with non-stationary, urgent demand, and a fixed staff size[J]. Journal of the Society for Health Systems, 1990, 2(2): 24-41.

[26]JAFARI H,SALMASI N.Maximizing the nurses′ preferences in nurse scheduling problem: mathematical modeling and a meta-heuristic algorithm[J]. Journal of Industrial Engineering International, 2015,11(3): 439-458.

[27]郝瑞.高校论文答辩系统的设计和实现[D].太原:太原理工大学,2007.

HAO R.Design and implementation of thesis defense system in colleges and universities[D].Taiyuan:Taiyuan University of Technology,2007.

[28]BUI L T, HOANG V.A multi-objective approach for master′s thesis committees scheduling using DMEA[M]. Berlin:Springer Berlin Heidelberg,2012.

A Thesis Oral Defense Scheduling Model and Its Application

FANG Gang, XU Zhe, GU Kun

(School of Economic Management, Beihang University, Beijing 100191, China)

Thesis oral defense scheduling is an important part of educational administration in colleges and universities. It has a direct influence on the fairness of review. Factors including characteristics and situations of oral defense scheduling, differences between reviewers who are in different research fields, time request of different reviewers, existing relationships between reviewers and respondents, the workload limit of reviewers who are assessing respondents′ thesis and the constraints that limit the number of reviewers and respondents of different groups have been considered. A two phase nonlinear integer programming model which includes group stage and reviewers′ assignment stage is built. Then a complexity analysis is executed which confirms that thesis oral defense scheduling problem is a NP-hard problem. The rationality and validity of the model are proved with an example using lingo mathematics software. It can be confirmed by the experiment that the model is helpful in improving the work efficiency of administrative staff and quality of defense management work.

educational administration management; oral defense scheduling problem; personnel rostering; nonlinear programming; integer programming

2016- 05- 10

国家自然科学基金资助项目(71571005，71271019)

方刚(1991-)，男，安徽省人，硕士研究生，主要研究方向为项目管理与调度.

10.3969/j.issn.1007- 7375.2016.06.019

C93

A

1007-7375(2016)06- 0123- 08