新课标下学生几何解题能力的提高途径探析

□李丽敏

新课标下学生几何解题能力的提高途径探析

□李丽敏

实行启发式教学有助于落实学生的主体地位和发挥教师的主导作用。面对学生比较“惧怕”的几何，如何“实行启发式教学”，从而提高几何解题能力，让学生在学习几何时体会成功、体会快乐，是本文的核心问题。故本文结合G·波利亚的解题思想，从多年实际教学经验出发，以具体例题为论证，提出了指导学生建构知识网络，在审题过程中“转换条件”和建立“基础题型库”等意见，在解题上“授之以渔”，以期提高学生的几何解题能力。

提高；几何解题能力；认知资源；基础题型库

一、引言

我们常说的“数学能力”，究竟体现在什么地方？笔者认为，一位学生的“数学能力”很大程度体现在“解题能力”上。学几何就意味着解几何题，解决几何问题是几何的核心。美国著名数学家G·波利亚说过：“问题是数学的心脏。” “掌握数学意味着什么？那就是善于解题。”“中学数学教学的首要任务就是加强解题训练。通过解题训练来培养解题能力，提高数学素养。”

几何，一直是学生比较“惧怕”的内容，如果能够在“解题能力”上有所提高，对于学生提高学习几何、学习数学的信心和兴趣，将会有很大的帮助。

二、实践探索

是什么原因造成了学生“解题技能”和“解题智能”发展不均衡？任教以来，在培养和提高学生几何解题能力方面，笔者进行了一些初步的探索。那么如何培养、提高学生的几何解题能力呢？笔者是从这两个方面去做的。

1.指导学生建构知识网络，审题过程中“转换条件”

美国数学教育学者舍费尔德提出：解题需要考虑四个变项：认知资源、启发法则、调控、信念系统。其中的认知资源是指：解题者拥有的与解题相关的数学知识，包括数学事实、运算程序及相关技巧等信息。

而笔者的学生是有相关的知识点，但没有检索出知识的思维程序。笔者认为，相关的知识点和思维程序就是舍费尔德提出的四个变项中的认知资源。

解几何问题，第一步，大家都知道是“认真审题”，但是数学题目里的文字学生都认识，题目读下来之后呢，“认真审题”究竟是审些什么？笔者指导学生“认真审题”包括三个步骤：

第一步：读条件，搜索脑海中的相关知识以及运算程序（思维程序），尽可能“转换条件”。

第二步：读问题，确定自己要解决该问题，需要什么。

第三步：“条件能得到的”与“问题所需要的”之间是否衔接上，还缺什么吗？

例如：如图1，△ABC内接于⊙O，AD是⊙O的直径，∠ABC=30°，则∠CAD=______。

图1

第一步：读到条件“AD是⊙O的直径”时，要想到“直径所对的圆周角是90°”，读到条件“∠ABC=30°”时，要能想到“一条弧所对的圆心角是它所对的圆周角的2倍”以及“同弧或等弧所对的圆周角相等”。

在圆里面，解决角的问题，基本的思维程序是：判断是否为圆心角或圆周角，如果是，找所对的弧，再找该弧所对的圆心角或圆周角。

圆心角或圆周角⇨所对的弧⇨所对的圆心角或圆周角。

条件“AD是⊙O的直径”转换为“∠ACD=90°”。

条件“∠ABC=30°”转换为“∠ADC=30°”。

第二步：看问题“∠CAD=____”，第①种想法：∠CAD是圆周角，可以通过所对的弧的圆周角或圆心角求得；第②种想法：在△ADC里，利用三角形内角和求。

第三步：第一步和第二步衔接，得解。

2.指导学生建立“基础题型库”

有学者将对数学解题过程的理解水平分为：不知其不知；知其不知；知其然但不知其所以然；知其然又知其所以然；知其何以所以然。在这一系列水平中，常被忽视的是“知其何以所以然”，即知道解题方法和思路是如何得到的。正如G·波利亚所讲的“老师的解题方法就像帽子里突然跑出一只兔子”，令人困惑不已.为了解决这个问题，G·波利亚对此进行了深入研究，得到了数学解题的一般策略，其中最重要的是自我启发的策略，产生了重大的影响。然而，策略中的“看是否做过此题”，却成为一些人使用“题海战术”和“套题训练”理由的“引经据典”，引发了新的问题。

笔者对G·波利亚的“看是否做过此题”这一策略的理解是：指导学生建立一个“基础题型库”。

在和学生一起解题的过程中，笔者发现，万变不离其宗，有很多看似新题，看似很难的题目，稍微转换一下条件，就变成前一阶段的题型。有些题型，随着新知识的学习，它会通过“改变条件呈现的形式”，一直贯穿在我们的题目中，笔者把这样的题型叫作“基础题型”。把具有代表性的“基础题型”指导学生归纳、概括起来，建立“基础题型库”，建立解题、表达的“情境”。

我们知道，学习语言，一个全世界都公认并提倡的好方法，就是建立丰富的语言情境（语境），让学习者在运用语言的过程中，一旦进入相应的语境中，马上就有感觉，就能自然而然地运用所学的语言。几何语言，也可以算是一门“新语言”，要帮助学生提高几何的解题能力，不能忽视“帮助学生掌握几何语言”这一环节，而这恰恰是我们很多数学老师忽略的环节。

建立“基础题型库”，就是帮助学生建立几何语言的“语境”。一旦学生进入到相应题型中，就像进入特定的“语境”中，这对学生的解题有很大的帮助。

比如，在学习“角平分线”和“平行的性质与判定”的内容后，有一道这样的题目：

如图2所示，已知∠1=∠2，AC平分∠BCD，试说明DC∥AB。

变式一：如图所示，已知DC∥AB，AC平分∠BCD，试说明∠1=∠2。

变式二：如图所示，已知DC∥AB，∠1=∠2，试说明AC平分∠BCD。

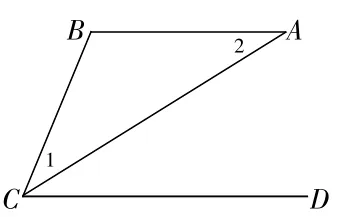
图2

这是一个基础题型。

学到“三角形的外角”时，有这样一道题目：

如图3，BE是△ABC的角平分线，DE∥BC交AB于点D，∠A=126°，∠BED=14°，求∠BEC的度数。

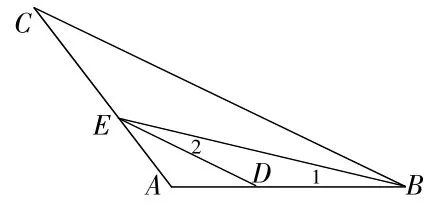
图3

题目所要求的∠BEC是△ABE的一个外角，即∠BEC=∠A+∠1

分析到这里，学生知道只要求出∠1，题目得解，这时，老师把AD、AE、CE擦掉，上述基础题型的变式一就呈现出来，学生进入熟悉的“情境”中解题.

学到“等腰三角形的判定时”，有这样一道题目：

如图4，在△ABC中，AB=AC，过∠ABC和∠ACB的平分线的交点O作DE∥BC，交AB与点D，交AC于点E，则图中共有_____个等腰三角形，他们分别是_____。

图4

其中，在判定△DBO和△ECO是等腰三角形时，图形的左、右两边各呈现了上述基础题型的变式一，学生再次进入熟悉的“情境”中解题。

学到 《四边形》中的 《矩形》，结合折叠，是一个常规的问题情境，有一道题如下：

如图5，已知长方形ABCD，沿对角线AC把△DAC翻折，使点D落在点D′处，AD′于BC交于点E。

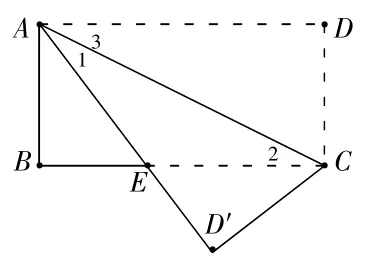
图5

①试判断△AEC的形状，并说明理由；

②已知AB=4cm，AD=8cm，求BE的长。

通过观察知道，△AEC应该是个等腰三角形，要证明这一结论，需要证明∠1=∠2，条件“折叠”转换为“∠1=∠3”（等同于条件“角平分线”），条件“矩形”转换为“AD∥BC”，上述基础题型的变式一又呈现出来，学生在熟悉的“情境”中解决新的问题。

学到“圆”，有这样一道题目：

如图6，AB是⊙O的直径，点D、C在⊙O上，AD∥OC，∠DAB=60°，连接AC，则∠DAC=_________。

图6

条件“⊙O”转换为“OA=OC”进一步得到“∠1=∠2”，把圆擦掉，呈现出上述基础题的变式二，学生又进入到熟悉的“情境”中解决新问题。

三、反思

当笔者从初一到初三完成一个循环后再回到初一，笔者意识到：要想帮助学生摆脱“茫茫题海”，要想帮助尽可能多的学生在数学学科体会到成功，帮助学生建立“脑海中有序的知识框架”很重要，怎么建立、怎么检测，则是主要问题，于是，笔者进行了以上的尝试，也取得了一定的成绩，但还有许多地方做得不尽如人意，还需要不断努力学习，不断深入探索，不断改进、完善。

[1]刘兼,孙晓天.数学课程标准解读[M].北京：北京师范大学出版社,2014.

[2]G·波利亚.怎样解题[M].上海：上海科技教育出版社,2011.

[3]俞平.数学教育心理学[M].南宁：广西教育出版社,2004.

（编辑：张 婕）

G633.63

A

1671-0568（2016）33-0096-02

李丽敏，中学数学一级教师，广东省中山市博爱初级中学，研究方向：课堂有效教学。