探究性学习方式在数学课堂中的应用案例

⌾廉继宗

(作者单位：甘肃省会宁县第一中学 730799)

探究性学习方式在数学课堂中的应用案例

⌾廉继宗

一、设计理念

《基础教育课程改革纲要》指出：“积极倡导自主、合作、探究的学习方式。”这个理念强调的是学习方式，而学习方式是学习者独立的个性化的行为，一般不受别人的支配或者外部的干扰，但课堂是师生共同活动相互交流的场所，师生的行为在这个特定的时空里是一种相互合作的团队行为，因此，既不能用教师教的方式替代学生学的方式，也不能用学生学的方式替代教师教的方式，应该把两种方式相互转化并有机地融合在一起，和谐地形成教学方式。

二、案例描述

参变量的求值(值域)问题在历年的考试中比较常见,由于其应用的广泛性和灵活性,已成为考试的热点。我在教学中总结归纳了参变量的求值(值域)问题的探究性教学的几种基本方法——

1.利用观察法求解 方程x2-a2x+a2-1=0有一根在(2，3)之间,求实数a的取值范围.

评析本题通过观察结构特征,找出了简捷解法.

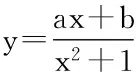
Y=0时,显然在函数值域[-1,4]内,带入方程(※)

得-ax-b=0由题意得:a≠0,若y≠0,则△=a2-4y(y-b)≥0的解集为[-1,0]∪(0,4),故-1,4是关于y的方程4y2-4by-a2=0的实根

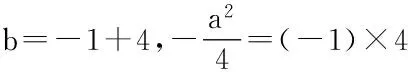
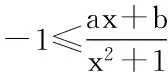
3.利用正难则反法求解 若下列方程:x2+4ax-4a+3=0,x2+(a-1)x+a2=0,x2+2ax-2a=0至少有一个方程有实根,试求实数a的取值范围.

分析三个方程至少有一个方程有实根的反面情况仅有一种:三个方程均没有实根.先求出反面情况时a的取值范围.所的范围的补集就是正面情况的答案.设三个方程均无实根,则有:

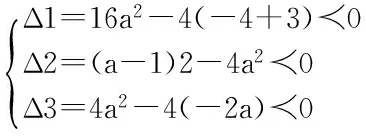
4.利用导数知识求解 已知函数f(x)=x3-ax2-3x,若f(x)在区间〔1,∞)上是增函数,求实数a的取值范围。

分析因为f(x)=x3-ax2-3a,所以,f’(x)=3x3-2ax2-3a又因为,

在区间〔1,∞)上是增函数,所以f’(x)在〔1,∞)上恒有

f’(1)=-2a≥0,所以a≤0

三、案例评析与反思

“问题解决”是当前中学数学教学改革中的一个热点问题。“问题解决”无论是作为教学目的，还是作为教学模式，或者看作一种数学能力，它的引进对中学数学教学改革都会注入新的活力。所谓数学问题的解决过程，实质上就是数学命题的不断变换和数学思想方法反复运用的过程，数学思想方法则是数学问题解决的观念性成果，它存在于数学问题的解决之中，数学问题的步步转化无不遵循数学思想方法指示的方向。因此通过数学问题解决，构造数学模型，提供数学想象，伴以实际操作，鼓励发散思维，诱发创造动机，就会把数学嵌入活的思维活动之中，并不断地使学生在做数学、谈数学、用数学的进程，学习知识、掌握方法、构造模型、形成创造性的数学思维能力。如在解题教学中，为了让学生在解题中有更广阔的思维空间，尝试进行“问题解决”式研究，可以改造一些常规性性题目，打破模式化，使学生不能依靠简单模仿来解决，如把条件、结论完整的题目改造成给出条件，先猜结论，再进行证明的形式；或给出多个条件，首先需要收集、整理、筛选以后才能求解证明，打破条件规范的框框。

创新能力主要指对新颖的信息、情境和设问，选择有效的方法和手段分析信息，综合与灵活地应用所学的数学知识、思想和方法，进行独立的思考、探索和研究，提出解决问题的思路，创造性地解决问题。学生数学创新能力是理性思维的高层次表现，对数学问题的“观察、猜测、抽象、概括、证明”，是发现问题和解决问题的重要途径，对数学知识的迁移、组合、融会的程度越高，显示出的创新能力就越强。

(作者单位：甘肃省会宁县第一中学 730799)