基于正交设计和神经网络的萃取精馏工艺优化

王洪海，张玉珍，李月，耿海腾，李春利

（1.河北工业大学化工学院，天津300130；2.天津市蓟县下仓镇人民政府，天津301905）

基于正交设计和神经网络的萃取精馏工艺优化

王洪海1，张玉珍1，李月1，耿海腾2，李春利1

（1.河北工业大学化工学院，天津300130；2.天津市蓟县下仓镇人民政府，天津301905）

通过优化精馏工艺的操作参数，得到最优操作参数组合，可实现萃取精馏过程的节能降耗．以溶媒原液二氯甲烷-乙醇-水混合液为研究物系，乙二醇为萃取剂，在Aspen中建立萃取精馏工艺模型进行研究．分别以二氯精馏塔、乙醇精馏塔塔顶产品纯度和塔釜能耗为目标函数，改变进料位置、理论板数、溶剂比和回流比等操作变量，通过正交设计、BP神经网络、径向基函数RBF神经网络模型进行优化对比，从而得到满足产品纯度、节能降耗的最优操作参数组合．结果表明通过神经网络建立的混合物系萃取精馏优化预测模型，能完成工艺的最优操作条件设计，且明显缩短优化工艺参数的时间，提高工艺设计效率，获得更优结果，约节能25％．

萃取精馏；BP神经网络；RBF神经网络；优化；节能

0 前言

精馏分离技术是化工分离过程中的重要部分，其分离机理和传热传质过程比较复杂，能量消耗是精馏分离得以实现的主要动力[1]．目前化工行业分离操作的能耗占化学工业总能耗的50％～70％，而精馏系统能耗占分离过程能耗的90％以上．因此，对精馏过程的节能和精馏工艺的优化研究具有非常重要的意义[2-3]．

精馏过程节能优化方法有：1）提高设备的系统传热效率；2）减少过程自身需要的能量；3）优化精馏过程操作参数．众多学者的研究证明在精馏系统中，通过Aspen Plus、HYSYS等流程模拟软件能有效的模拟工艺流程并能指导工业应用．而对精馏工艺流程的优化，朱登、Wang、Luyben、王震等人[4-7]利用流程模拟软件自带的分析工具进行单因素分析，分别改变理论板数、进料位置、回流比、溶剂比等操作参数，得到较优操作参数．而精馏系统是多输入多输出多变量、内在机理复杂、参数耦合严重的过程，仅单因素优化往往出现局限性．针对这个问题，宋海华等[8]采用人工神经网络（ANN）与ASPEN软件相结合的方法来模拟乙酸与乙醇酯化的反应精馏过程,建立操作变量与控制变量之间的函数关系，结果表明ANN预测模型具有很高的精度．陈心路等[9]对于四塔甲醇精馏提出了一种采用3层BP神经网络的拟合方法，并对拟合出的函数运用遗传算法求出最优操作参数，达到节能降耗，为精馏过程的优化提供了更有价值的参考方案．萃取精馏过程具有变量多、非线性程度强、优化起来难度较大等特点．而文献[10]证明采用BP神经网络建立萃取精馏分离甲醇-丙酮-水混合体系预测模型，能够很好地反映参数组合与目标函数之间的关系，能较大程度地达到节能的效果．

人工神经网络是在1943年由心理学家M cculloch和数学家Pitts最早提出的，在优化应用方面很大一部分来自数学统计学，其应用特点是：在没有精确的数学模型的情况下，能够利用软件创建神经网络并行计算、从输入输出的数据中学习相关规则、实现非线性映射等[11-14]．本文以二氯甲烷-乙醇-水混合物系为研究对象，建立萃取精馏模型后，通过正交设计实验、BP神经网络、RBF神经网络等方法进行预测模拟与优化设计，比较不同预测模型的优化结果，得到最低能耗下的最优操作参数组合，并验证所建立模型的可行性，避免了选择最优操作参数的局限性．

1 萃取精馏工艺流程

溶媒原液各组分含量为二氯甲烷（质量分数）80％，乙醇17％，水3％，要求对该混合物中的二氯甲烷和乙醇分离回收再利用．待分离物系中二氯甲烷与乙醇（共沸点54.6℃）、二氯甲烷与水（共沸点38.1℃），乙醇与水（共沸点78.15℃）两两之间均形成共沸物，选择乙二醇作为萃取剂，进行萃取精馏分离[15-16]．在Aspen plus中建立工艺流程，热力学模型选用NRTL方程[17-18]，工艺流程如图1所示．

原料液进料量为100 kg/h，温度20℃，常压操作下，二氯精馏塔在塔顶得到高浓度二氯甲烷和少量水，馏出的含水二氯甲烷经冷凝后进入分相罐中静置分相，下层得到质量分数＞99％二氯甲烷．二氯精馏塔塔釜中是乙醇和水混合物，以流量18.2 kg/h，温度78.5℃采出并作为乙醇常压精馏塔进料，进行分离．在乙醇精馏塔塔顶馏出质量分数＞99.5％的乙醇，塔釜是乙二醇和水的混合物，其作为进料进入乙二醇减压塔．在乙二醇塔塔釜得到高纯度乙二醇，作为循环萃取剂进入乙醇塔中重复使用．

二氯精馏塔操作条件：理论板数20，原料进料位置为第17块理论板，回流比为1.8．乙醇精馏塔操作条件：理论板数12，回流比1.4，原料进料位置为第11块理论板，溶剂进料位置第2块理论板，溶剂比为1.1．

分别以两塔理论板数、进料位置、回流比、溶剂比、萃取剂进料位置为操作变量，以二氯精馏塔二氯甲烷含量、塔釜的能耗和乙醇精馏塔乙醇含量、塔釜能耗为目标函数进行单因素优化分析，并通过实验验证了优化结果的准确性，结果如表1所示．

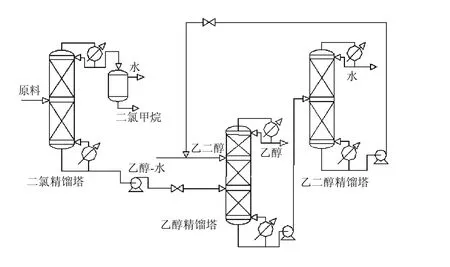
图1 工艺流程图Fig.1 The flowsheetof distillation simulation

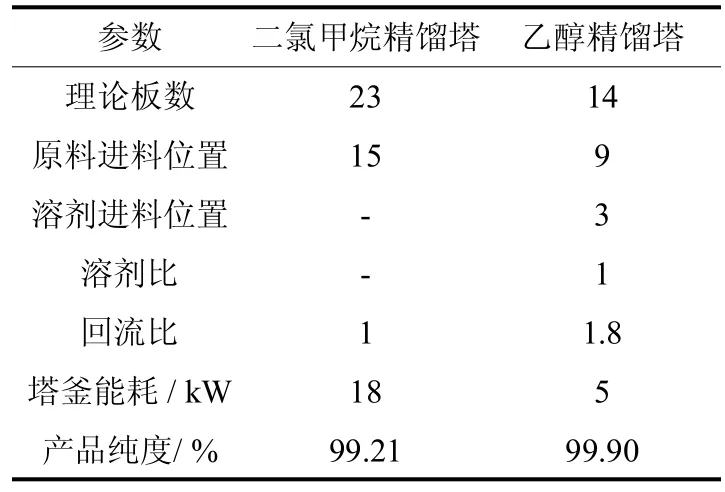
表1 单因素分析结果Tab.1 Single factoranalysis results

2 二氯精馏塔的优化

2.1 正交实验设计

2.1.1 二氯精馏塔的正交优化

分别以精馏塔塔顶二氯甲烷含量和塔釜的能耗为目标函数，以理论板数（A），进料位置（B），回流比（C）为操作变量，通过正交设计（OrthogonalDesign）[19]可以设计一个3因素5水平的正交实验，用极差直观分析法分析实验结果．3个因素的5个水平实际值如表2所示．

表2 正交设计因素与水平Tab.2 Factorsand levelsof orthogonaldesign

采用L25（56）正交表，以3因素5水平设计了25组实验，目标函数为二氯精馏塔塔顶二氯甲烷的质量分数，实验结果如表3所示．

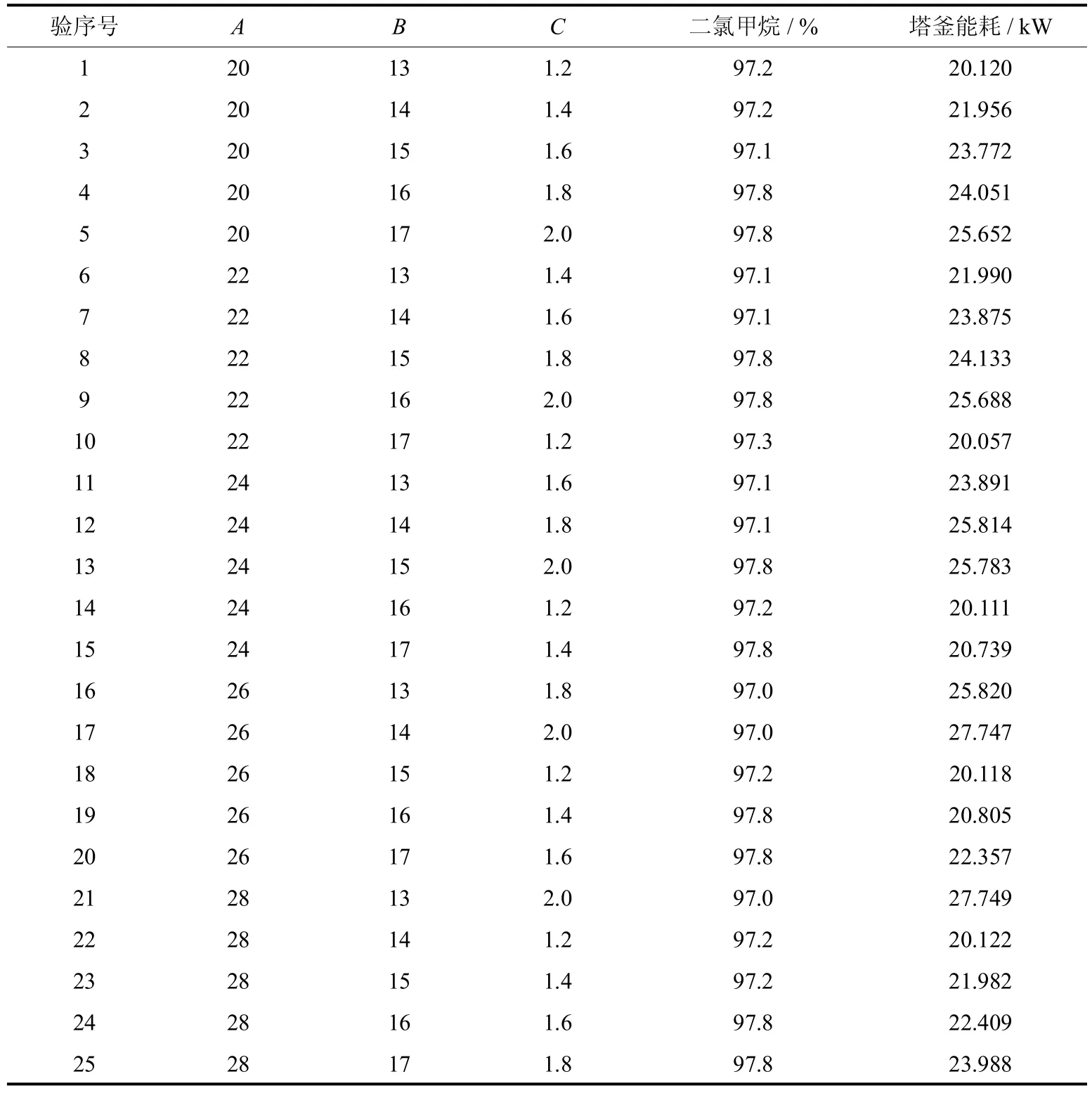
表3 以二氯甲烷含量为目标函数的正交试验设计及模拟结果Tab.3 Orthogonaldesign and resultsofmass fraction of dichloromethane asobjective function

2.1.2 二氯精馏塔正交试验设计的极差分析

25次实验结果中有10次实验的二氯甲烷质量分数达到了97.8％，经过后期工序，料液送入分相罐中冷却分相后，产品二氯甲烷的含量可达到99％以上．通过对结果的直观分析，找到较优的水平组合，步骤如下．

计算每个因素在不同水平下质量分数平均值．

表3中“T1j”行给出在理论板数A1=20块时，5次试验的二氯甲烷质量分数之和

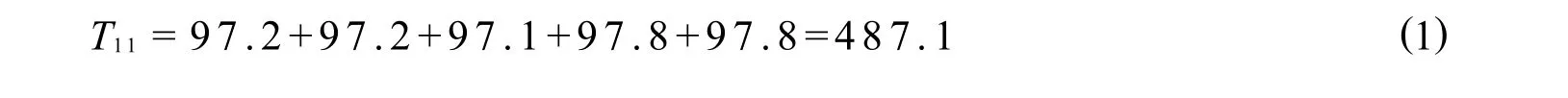
其平均值为M11，列于“M1j”行的第1列处

因素极差值的计算

每个因素的计算结果如表4所示，其中：j=1,2,3；Rj为极差．

通过表4数据，由极差大小排列因素由主到次的顺序为BCA，可以得出较优的操作条件为A1B5C4．即二氯甲烷精馏塔理论板数为20块板，原料进料位置为第17块板，回流比为1.8．此时目标函数塔顶二氯甲烷质量分数99.10％，塔釜能耗为24.01 kW．以塔釜为目标函数时，采用同样的分析计算方法得到的结果如表5所示．

表5 以塔釜能耗为目标函数的极差分析Tab.5 The range analysisof the reboiler duty asobjective function

通过表5数据，由极差大小排列因素由主到次的顺序为CBA，可以得出较优的操作条件为A1B3C1．即二氯甲烷精馏塔理论板数为20块板，原料进料位置为第15块板，回流比为1.2．此时目标函数塔顶二氯甲烷质量分数98.60％，塔釜能耗为20.07 kW．

2.2 二氯精馏的神经网络数学模型

2.2.1 BP网络数学模型

分别对二氯甲烷质量分数和塔釜能耗2个目标函数，利用函数newff创建单隐层BP神经网络，且输入参数都为3个，目标函数为1个．输入层到隐含层的传递函数为tansig，隐含层节点数为6，训练函数为trainbr，输出函数为purelin．这样一个输入矢量(由训练样本提供)经过隐含层的一系列变换，然后得到一个输出矢量，从而实现输入数据与输出数据间的一个映射关系[20]．

构建的BP神经网络的输入层阈值和权值设定：

InputWeights=net.IW(1,1)；Inputbias=net.b；

网络层阈值和权值设定：

layerWeights=net.IW(2,1)；layerbias=net.b(2)；

训练参数设置为：

net.trainParam.show=100；net.traiTiParam.lr=0.01；net.trainParam.mc=0.9；

net.trainParam.epochs=2 000；net.trainParam.goal=0.01；net.trainParam.m in_grad=1e-20

以表3中的25组数据为训练样本，在MATLAB软件中运行BP神经网络程序，进行反复的学习训练并且通过误差的反向传播来修改连接权系数，采用最速下降法，使误差函数收敛于该函数的最小点[21]，得到塔顶二氯甲烷含量的BP神经网络．其输入层到隐含层的权值W11和阈值B11，如式(5)、式(6)所示

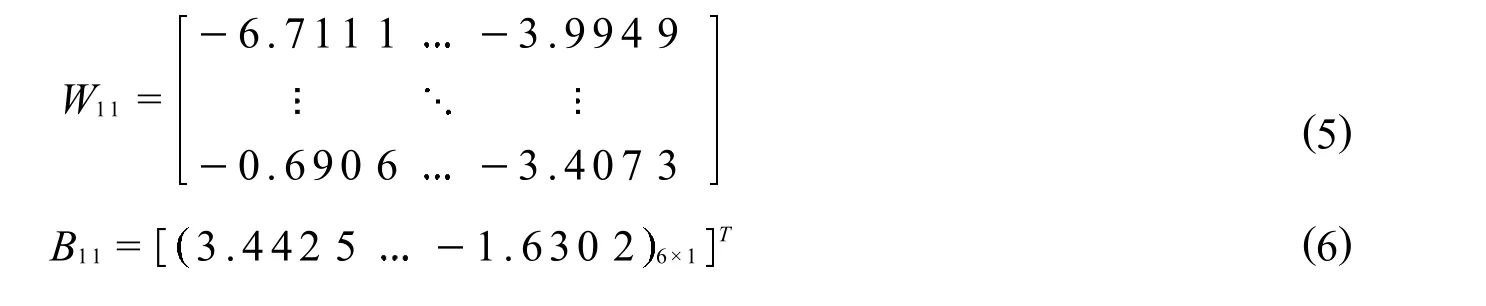
网络输出层的权值W12和阈值B12，如式(7)、式(8)所示

在网络训练过程中，收敛情况如图2所示，第15次迭代时，达到最小均方误差4.17×109，误差的下降梯度为0.000 179，满足预测精度要求．

以塔釜能耗为目标函数的网络训练过程中，塔釜能耗的BP神经网络输入层到隐含层权值W21和阈值B21，如式(9)、式(10)所示．

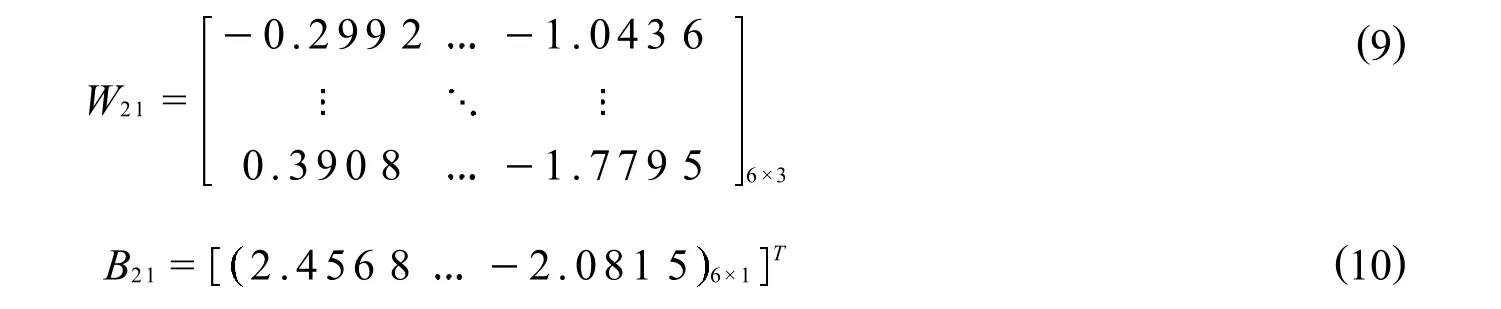
塔釜能耗的BP神经网络隐含层权值W22和阈值B22，如式(11)、式(12)所示

收敛情况如图3所示，在第25次迭代时，达到最小均方误差8.98×106，误差的下降梯度为0.000235，满足预测精度要求．

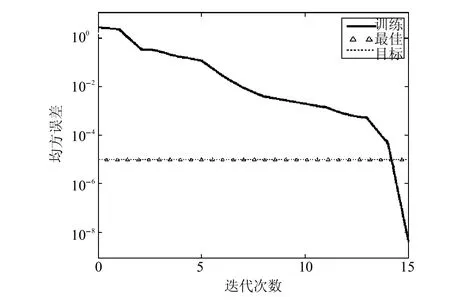
图2 二氯甲烷含量BP网络训练结果Fig.2 The BPnetwork training resultsof dichloromethane

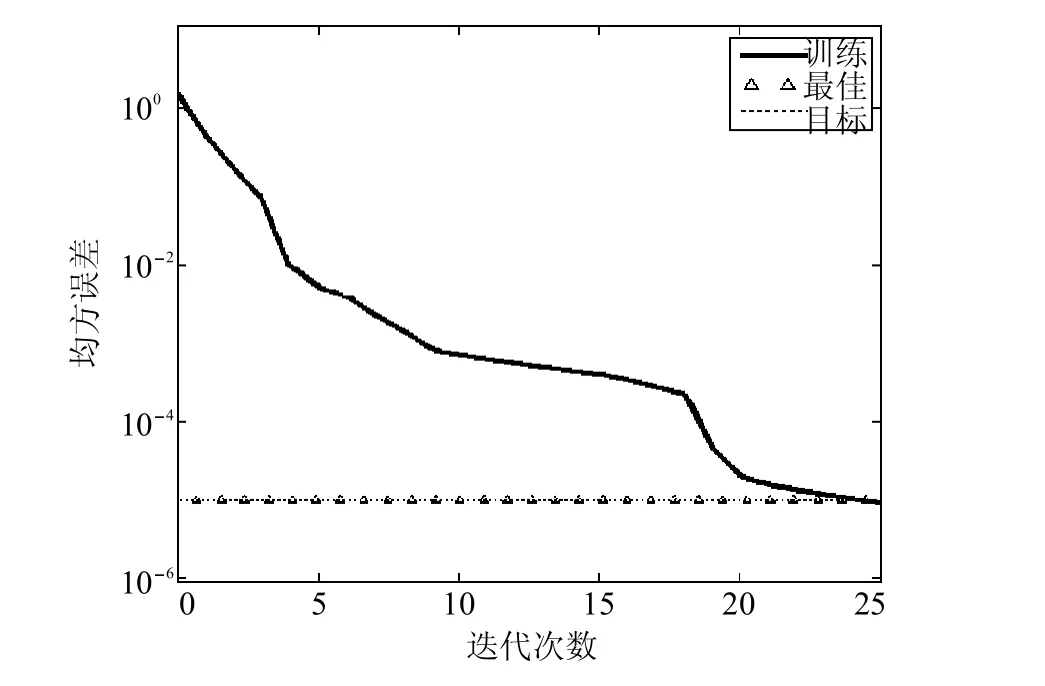
图3 塔釜能耗BP网络训练结果Fig.3 The BPnetwork training resultsof reboiler purity

2.2.2 RBF网络数学模型

RBF神经网络对比于BP神经网络，隐含层的神经元数目，网络逼近能力、分类能力和学习速率等方面均较优于BP神经网络[22]．利用MATLAB中的newrb创建RBF神经网络，隐含层激励函数为radbas，加权函数为dist，输入函数为netprod，输出层神经元函数为线性函数purelin，加权函数为dotprod，输入函数为netsum．输入层是3个节点，即A、B、C 3个影响因素，输出层是1个节点，对应二氯甲烷含量，在创建过程中，需要不断增加中间层神经元个数，直到网络的输出误差满足预先设定的值为止．RBF神经网络的参数设置：

spread=1.2；

[net,tr]=new rb(P,T,0,1.2，25，20)．

在训练过程中不断调整神经元连接权值，达到神经网络的预测误差最小化的性能指标．将表3中的25组数据作为训练样本输入RBF网络进行训练．在MATLAB中运行程序．塔顶二氯甲烷含量的RBF神经网络输入层网络权值W31和阈值B31，如式(13)、式(14)所示

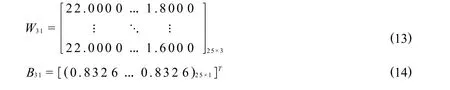
塔顶二氯甲烷含量的RBF神经网络隐含层权值W32和阈值B32，如式(15)、式(16)所示

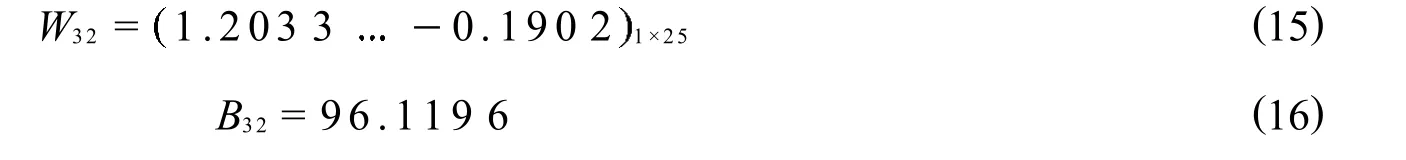
塔顶二氯甲烷含量的RBF神经网络创建过程中的误差曲线如图4所示，当中间层神经元个数增至25时，网络输出误差小于1025，故RBF神经网络的预测效果满足精度要求．

塔釜能耗的RBF神经网络输入层权值W41和阈值B41，如式(17)、式(18)所示

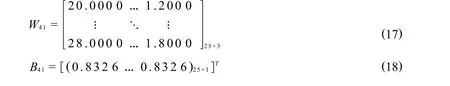
塔顶二氯甲烷含量的RBF神经网络隐含层权值W42和阈值B42，如式(19)、式(20)所示

塔釜能耗的RBF神经网创建过程的误差曲线如图5所示．同样当中间层神经元个数增至25时，网络输出误差小于1025，故RBF神经网络的预测效果满足精度要求．

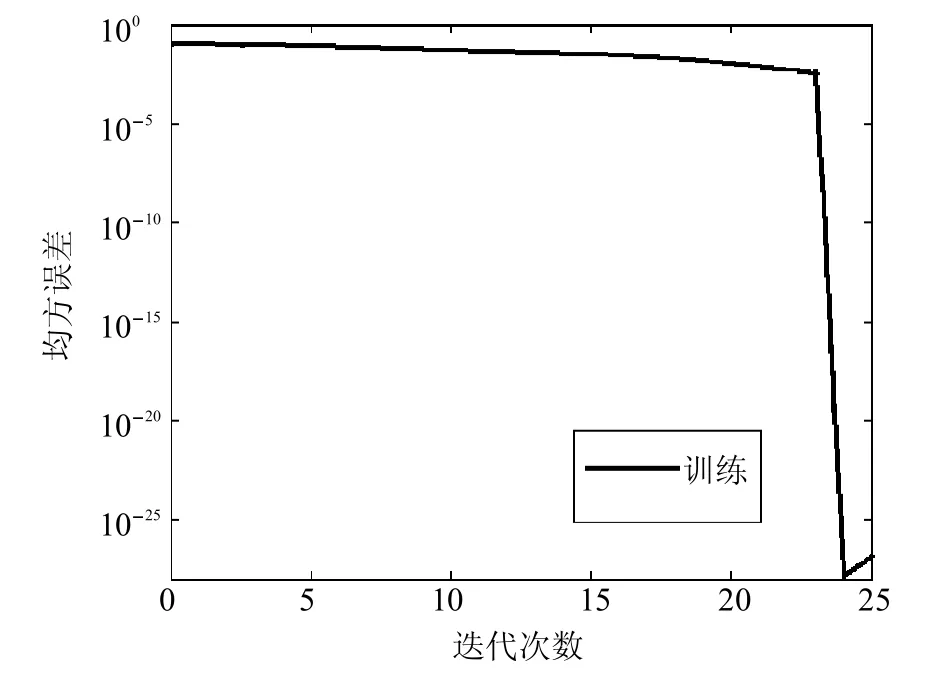
图4 二氯甲烷含量RBF网络建立过程的误差曲线Fig.4 The RBFnetwork error curveof dichloromethane purity

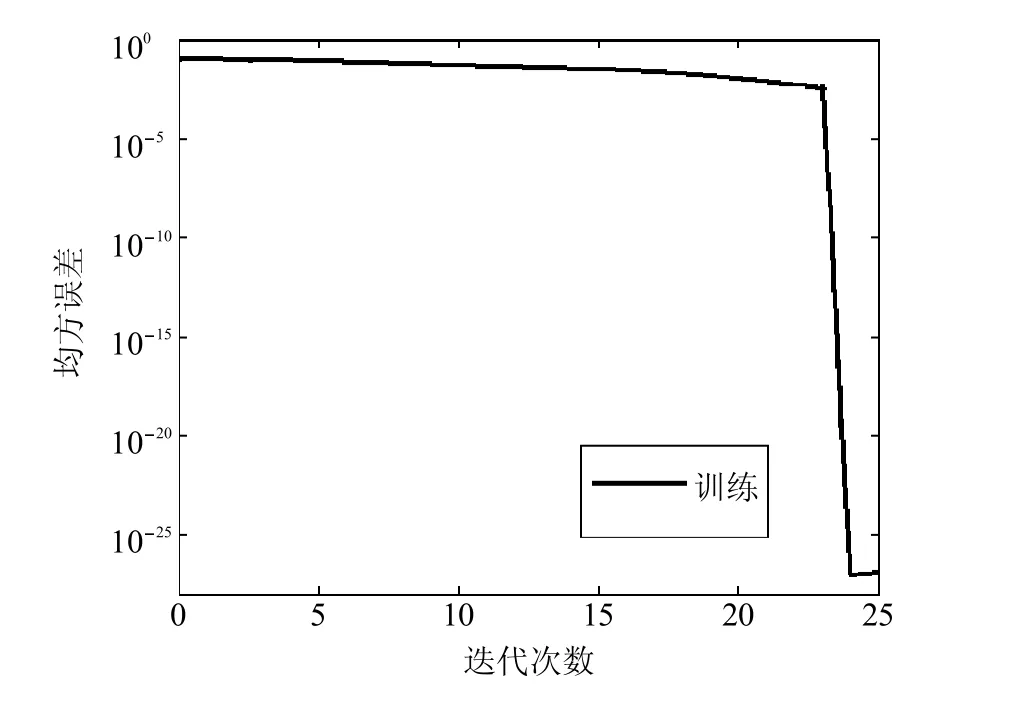
图5 塔釜能耗RBF网络建立过程的误差曲线Fig.5 The RBFnetwork error curveof reboiler duty

2.3 结果与讨论

利用所建立的塔顶二氯甲烷含量和塔釜能耗的BP和RBF网络模型对各影响因素的变化进行预测，并将模拟值与预测值进行比较，如表6所示．

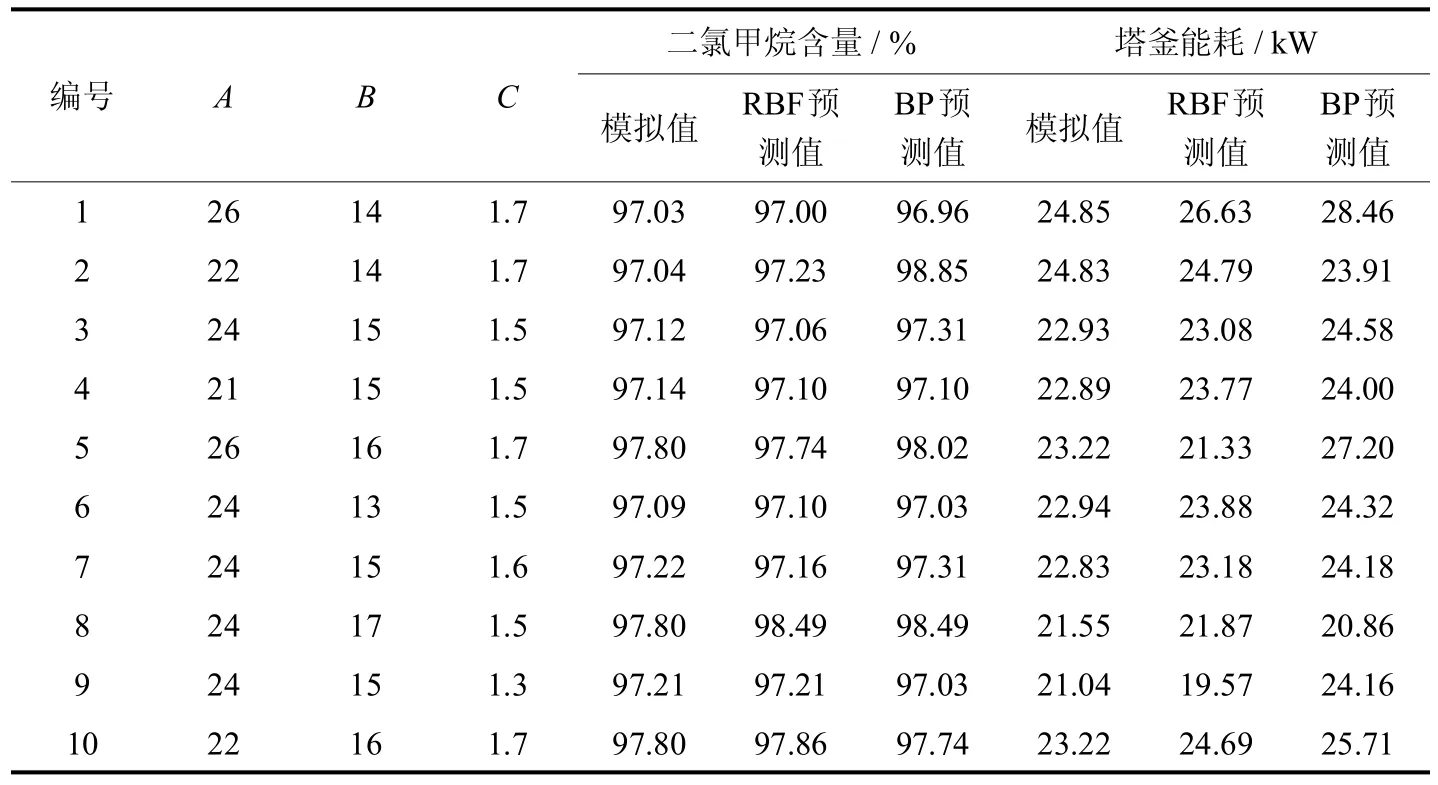
表6 塔顶二氯甲烷含量和塔釜能耗的预测值与模拟值的比较Tab.6 Comparison of dichloromethane contentand the reboiler duty predicted valuesand simulation values

通过表6中的数据可以看出，RBF网络建立的模型精度更高，所得的预测值与流程模拟值更加接近．

为了满足塔顶二氯甲烷含量的工业要求，同时实现塔釜的低能耗，需要将二氯甲烷含量的RBF网络模型和塔釜能耗的RBF模型相结合求解，从而求出最优的操作参数．对于多变量有约束的非线性问题的求解，可以使用MATLAB中的fmincon函数．设置目标函数为塔釜能耗的RBF网络模型，求解其最小值．并以塔顶二氯甲烷含量RBF网络模型为约束条件，要求二氯甲烷含量大于99％．经过计算，得到优化结果为：二氯精馏塔理论板数为20，原料进料位置为第11块板，回流比为1.0．此时，塔顶二氯甲烷质量分数为99.28％，塔釜能耗为18.25 kW．

正交设计法优化结果与人工神经网络的优化结果对比如表7所示．从中可以看出用RBF神经网络方法优化后，在较优操作参数下，产品纯度更高，能耗更小．

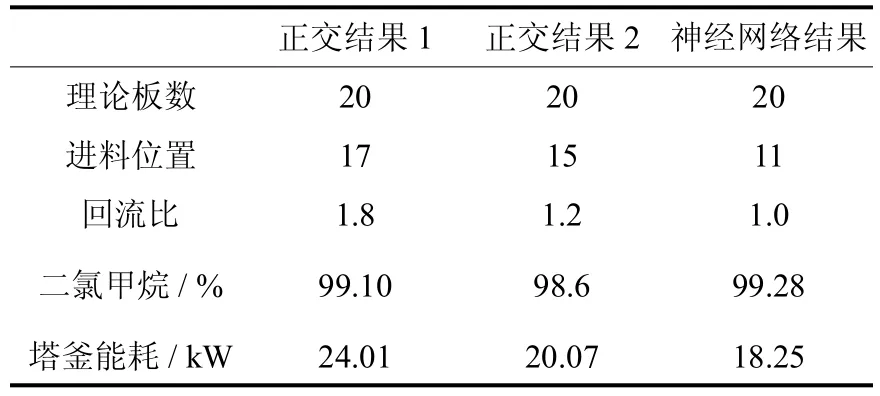
表7 结果比较Tab.7 Comparison of results

3 乙醇精馏塔的优化

3.1 正交设计实验

考察乙醇萃取精馏塔理论板数（A）、原料进料位置（B）、回流比（C）、萃取剂进料位置（D）、溶剂比（E）等5个因素对目标函数乙醇塔塔顶产品乙醇含量以及塔釜能耗的影响，采用L25（56）正交表，设计5因素5水平25组正交试验．以乙醇精馏塔的乙醇质量分数为目标函数，做极差计算，可以得出较优的操作条件为A1B4C4D3E5．即乙醇精馏塔理论板数为12块板，回流比为1.4，原料进料位置为第11块板，萃取剂进料位置为第4块板，溶剂比为1.1．此时目标函数塔顶乙醇质量分数达到99.97％，塔釜能耗1.428 kW．以乙醇精馏塔塔釜能耗为目标函数，做极差计算，由极差大小排列因素由主到次的顺序为CEDBA，可以得出较优的操作条件为A4B1C1D2E1．即乙醇精馏塔理论板数为15块板，回流比为1.0，原料进料位置为第8块板，萃取剂进料位置为第3块板，溶剂比为0.7，此时目标函数塔顶乙醇质量分数达到99.80％，塔釜能耗为0.97 kW．

3.2 乙醇塔的神经网络数学模型

以设计的5因素5水平25组正交实验数据为基础，分别训练MATLAB中构建的乙醇塔BP神经网络模型、RBF神经网络模型．通过训练，分别得到BP神经网络模型和RBF神经网络模型中，以塔顶乙醇含量和塔釜能耗为目标的输入层权值和阈值．从而，建立完善的乙醇塔的神经网络预测模型．

3.3 结果与讨论

利用已建立的乙醇精馏塔塔顶乙醇含量的BP和RBF网络模型进行预测，并将模拟值与预测值进行比较，如表8所示．

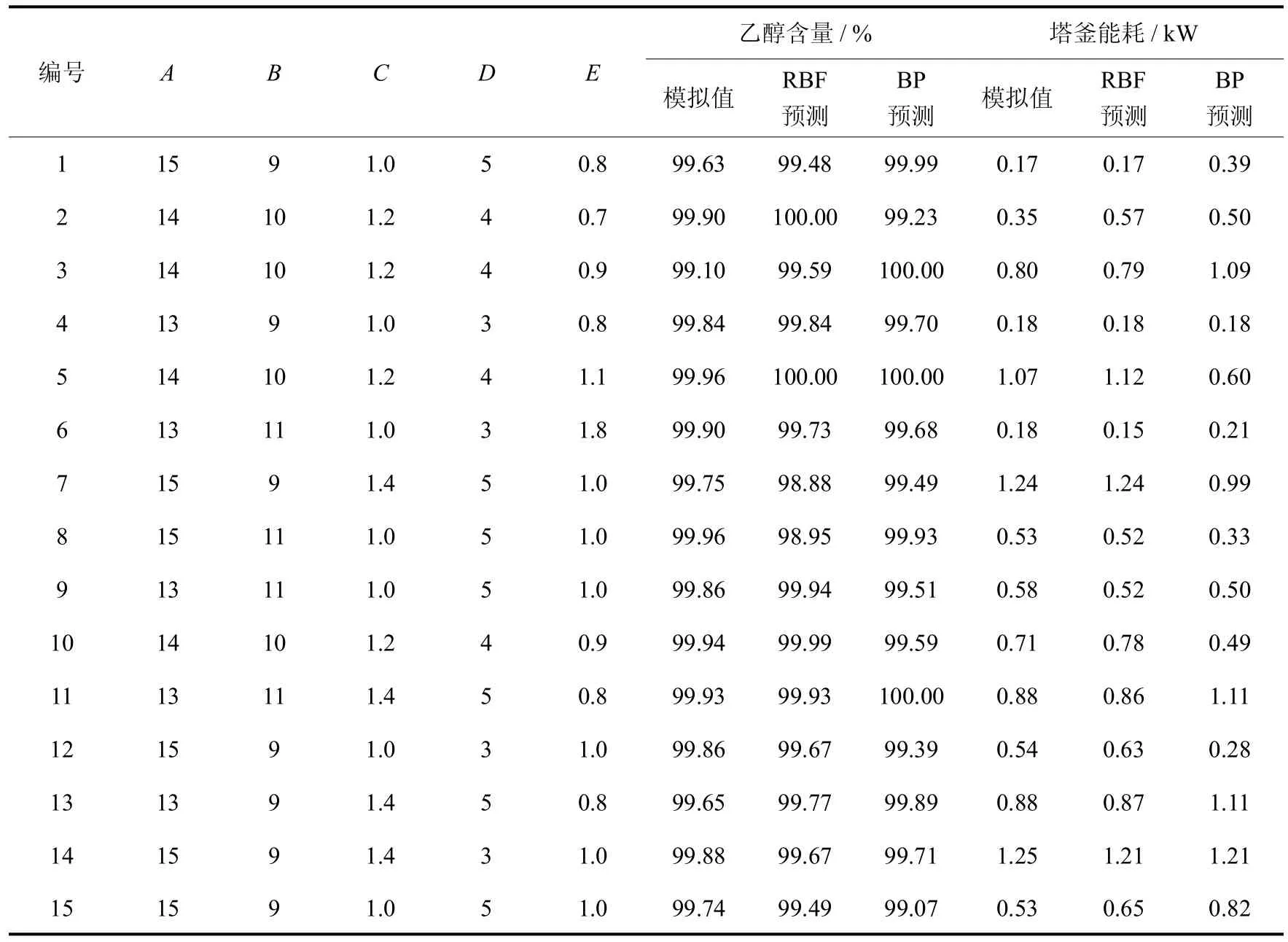
表8 塔顶乙醇含量和塔釜能耗的预测值与模拟值的比较Tab.8 Comparison of ethanol contentand the reboilerduty predicted valuesand simulation values

通过表8中的数据比较可得，RBF网络建立的模型更准确，预测值与流程模拟值更加接近．

求解同时满足乙醇含量达到工业要求和塔釜能耗较低2个要求的操作参数．塔釜能耗作为RBF网络模型的目标函数，求解其最小值，并以塔顶乙醇含量作为RBF网络模型的约束条件，要求乙醇含量大于99.5％．使用MATLAB中的fmincon函数求解，可以得到优化结果为：乙醇精馏塔理论板数为16块，原料进料位置为第10块板，回流比为1.5，萃取剂进料位置为第2块板，溶剂比为0.7．塔顶乙醇质量分数为99.81％，塔釜能耗为0.78 kW．

正交设计法优化结果与人工神经网络优化的参数和结果进行比较，如表9所示．从中可以看出神经网络方法优化出最佳参数组合的能耗更小．

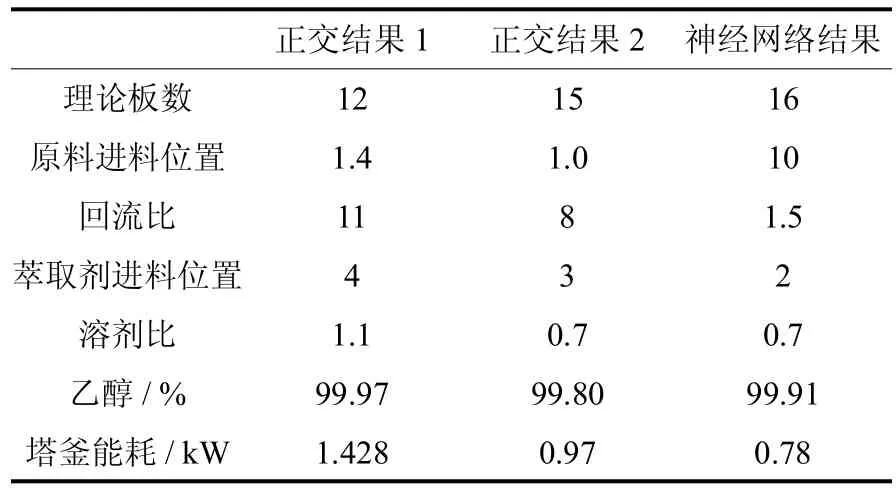
表9 结果比较Tab.9 Comparison of results

4 结论

1）利用正交设计和人工神经网络2种方法进行寻优，选出了较优的操作参数．对于二氯甲烷精馏塔，以塔顶二氯甲烷质量分数作为目标函数时，利用RBF神经网络建立优化模型，选出较优结果，二氯甲烷质量分数为99.28％，塔釜能耗为18.25 kW．对于乙醇精馏塔，以塔顶乙醇质量分数作为目标函数，利用RBF神经网络建立优化模型，选出较优结果，乙醇质量分数为99.71％，塔釜能耗为0.78 kW．

2）对于多变量的精馏过程，建立输入为理论板数，进料位置，回流比，溶剂进料位置和溶剂比等工艺参数，输出为产品质量分数和塔釜能耗的映射关系模型，需要计算大量数据，而这些数据用统一的规则或者公式描述比较困难，无法用数学模型来表示．人工神经网络以其极大的灵活性和自适应性成为解决这一问题的有利工具．以上分析表明：将神经网络与正交试验二者结合用于二氯甲烷-乙醇-水物系的精馏工艺参数优化过程中，避免了单因素优化的局限性，可以明显缩短优化工艺参数的时间，提高工艺设计效率，具有获得全局最优解的能力．而RBF神经网络建立的预测模型能获得比正交试验更优的结果，实现节能约25％．

[1]Engelien HK，Skogestad S．Selecting appropriate control variables for a heat-integrated distillation system w ith prefractionator[J]．Comp Chem Eng，2004，28（5）：683-691．

[2]Matsuda K，KawazuishiK，Kansha Y，etal．Advanced energy saving in distillation processwith self-heat recuperation technology[J]．Energy，2011，36（8）：4640-4645．

[3]佟昊，董守亮．影响精馏操作的主要因素及精馏节能技术浅析[J]．中国石油和化工标准与质量，2012，33（12）：29．

[4]朱登磊，谭超，任根宽．基于Aspen Plus萃取精馏的概念设计及优化[J]．计算机与应用化学，2010，27（6）：791-795．

[5]Wang H，Cui X，Li C，et al．Separation of ethyl acetate-dichloromethane-ethanol by extractive distillation：simulation and optimization[J]．Chem ical Engineering＆amp;Technology，2013，36（4）：627-634．

[6]LuybenW L．Comparison ofextractivedistillation and pressure-sw ing distillation foracetone/chloroform separation[J]．Computers＆amp;Chem icalEngineering，2013，50（5）：1-7．

[7]王震，高晓冲，夏庆宁，等．萃取精馏分离二氯甲烷-丙酮的工艺模拟[J]．精细石油化工，2012，29（4）：54-57．

[8]宋海华，宋高鹏，宋静，等．多目标遗传算法在反应精馏优化中的应用[J]．化学工业与工程，2008，25（1）：52-55．

[9]陈心路，赵霞，建宁．基于神经网络的精馏能耗模拟和优化[J]．计算机技术与发展，2011，21（6）：173-176．

[10]王洪海，梁建成，催小英，等．BP神经网络优化在萃取精馏体系上的应用[J]．现代化工，2015，35（7）：154-158．

[11]Hagan M T，Demuth H B，BealeM H．Neuralnetwork design[M]．Boston：Pws Pub，1996．

[12]高隽．人工神经网络原理及仿真实例[M]．北京：机械工业版社，2003，7．

[13]贾光峰．基于多表达式编程的神经网络自动优化方法及其应用研究[D]．济南：济南大学，2009．

[14]魏海坤．神经网络结构设计的理论与方法[M]．北京：国防工业出版社，2005．

[15]汪晓强，李勤涛，陈红，等．间歇萃取精馏分离乙醇-水萃取剂的评选研究科[J]．科学技术与工程，2013，13（21）：6312-6314．

[16]Benyahiak，BenyounesH，ShenWF．Energyevaluationofethanoldehydrationwithglycolmixtureasentrainer[J]．Chem icalEngineering＆amp;Technology，2014，37（6）：987-994．

[17]范天博，王利生．应用NRTL和UNIQUAC模型计算含全氟烃体系液液相平衡[J]．北京化工大学学报（自然科学版），2006，33（5）：18-22．

[18]徐建新，张洪起，刘继东，等．电解质NRTL模型的研究进展及应用[J]．化工进展，2013（9）：2023-2029．

[19]刘达民，程岩．应用统计[M]．北京：化学工业出版社，2004．

[20]沈学利，张红岩，张纪锁．改进粒子群算法对BP神经网络的优化[J]．计算机系统应用，2010，19（19）：57-61．

[21]孙娓娓，刘谅荪．BP神经网络的联合优化[J]．计算机工程与应用，2009，45（12）：50-51．

[22]张德封．MATLAB神经网络编程[M]．北京：化学工业出版社，2011．

[责任编辑 田丰 夏红梅]

Theorthogonaldesign and neuralnetwork optim ization of the extractive distillation process

WANG Honghai1，ZHANG Yuzhen1，LIYue1，GENG Haiteng2，LIChunli1

(1.School of Chem ical Engineering,Hebei University of Technology,Tianjin 300130,China;2.People's Government of Xiacang Town JiXian County,Tianjin 301905,China)

Theextractive distillation processusing theextraction solventethyleneglycol to separate the dichloromethaneethanol-waterm ixturewasperformed in Aspen Plus.In order togettheoptimum combination ofparametersandm inim ize theenergy consumption in theextractivedistillation system,we choose theproductpurity in theoverhead and the reboiler duty as the objective functions to investigate the effects of feed location,number of theoretical plates,solvent ratio, reflux ratio and other interactions.The system wasoptim ized using the orthogonaldesign,BPartificialneuralnetwork model and RBF artificial neural network model.Simulation results indicate that the better combinations of parameters were obtained and the efficiency of process design was improved by establishing the neural network predictionmodel. The energy efficiency hasbeen improved by 25％compared w ith the former process.

extractive distillation;BPneuralnetwork;RBFneuralnetwork;optim ization;energy saving

TQ028

A

1007-2373(2016)03-0048-09

10.14081/j.cnki.hgdxb.2016.03.009

2015-12-10

河北省重点基础研究项目（15964505D，16214505D）

王洪海（1974-），男（汉族），教授，博士．通讯作者：李春利（1963-），男（汉族），教授．