关于S-亚紧空间的一些结果

彭知南，朱培勇

(电子科技大学数学科学学院，四川 成都 611731)

关于S-亚紧空间的一些结果

彭知南，朱培勇

(电子科技大学数学科学学院，四川 成都 611731)

对S－亚紧空间的一些性质进行研究，得到如下一些结果:(1)拓扑空间X是S－亚紧的当且仅当X的每一个定向开覆盖都有点有限的半开加细.(2)设X，Y是拓扑空间，f:X→Y是完备的优柔映射.如果Y是S－亚紧的，则X也是S－亚紧的.(3)设X是一个S－亚紧空间，如果Y是紧空间，则X×Y也是S－亚紧空间.

S－亚紧空间；完备映射；优柔映射；定向开覆盖；点有限半开加细

1 引言及预备知识

1963年，Levine.N引入半开集的概念[1]，特别是半拓扑性质和S-闭空间的引入，使得半开集理论成为近代一般拓扑学中较为活跃的专题。近年来，利用半开集，从半覆盖，类比紧性，出现了S-紧性.2006年，K.Y.AL-ZOUBI[2]引入了S-仿紧空间的概念并且对其性质进行了研究；2014年，文献[3]在S-仿紧空间的基础上提出了S-亚紧空间的概念，并且得到了一部分相关的性质，但没有给出在一般拓扑空间下S-亚紧的等价刻画。受这些启发，本文对S-亚紧空间作了进一步研究，给出了S-亚紧空间的一个等价刻画，并且将S-仿紧空间的一些性质有效的推广到S-亚紧空间上，并讨论它的性质，得到了一些结果.

设X是一个拓扑空间，集合A是X的子集，为了方便，本文用int(A)、cl(A)分别表示A的内部与闭包，用SO(X)表示由X中所有的半开集构成的集族，并且∅表示空集，N表示自然数集.

定义1 X是一个拓扑空间，集合A是X的一个子集，集合A称为半开集，如果在X中存在开集U，使得U⊆A⊆cl(U)[1].

由上定义不难得到:A为半开集当且仅当A⊆cl(int(A)).

定义2 设ξ，η是X的子集族:

(1)η是ξ的部分加细，若∀B∈η，∃A∈ξ，使得B⊂A；

(2)η是ξ的加细，如果η是ξ的部分加细且∪η＝∪ξ[4]；

(3)设ξ＝{Aα｜α∈Λ}，称η在点x∈X是点有限的，若{α∈Λ｜x∈Aα}是有限的；

(4)称ξ在X上是点有限的，如果ξ在每一个点x∈X是点有限的.

定义3 设X是一个拓扑空间，X称为S-亚紧空间，如果X的每一个开覆盖都有一个点有限的半开加细[3].

定义4 设(X，T)，(Y，M)都是拓扑空间，f:X→Y是一个映射:

(1)f称为完备(Perfect)的映射[5]，如果f是一个连续闭映射，并且对于任意的y∈Y，有f－1(y)是X的紧子集；

(2)f称为优柔映射[6]，如果对于任意的G∈SO(Y，M)，有f－1(G)∈SO(X，T).

引理5 设A是拓扑空间上的开集，V∈SO(X，T)，则A∩V∈SO(X，T)[6].

定义6 设X为拓扑空间，U为X的一个覆盖，称U为X的一个定向覆盖，如果任意的有限子集族V⊂U，有∪V∈U[7].

拓扑空间X称为是T2空间[7]，若X中任意两个不同点x与y，存在U∈U(x)，存在V∈U(y)，使得U∩V＝φ.此外，本文所涉及到的其他概念和符号，如果没有特别声明都来自于文献[4]与文献[7-17].

2 主要结果及证明

首先，在之前一些学者对仿紧、亚紧，S-仿紧、S-亚紧等空间的刻画性质广泛研究的基础上，类似地，给出S-亚紧空间的一个刻画，性质如下:

定理1 一个拓扑空间X是S-亚紧的当且仅当X的每一个定向开覆盖都有点有限的半开加细.

证明 (充分性)设U＝{Uα｜α∈Λ}为X的一开覆盖，UF＝{∪α∈σUα｜σ∈[Λ]＜ω}，其中[Λ]＜ω表示Λ的所有有限子集的集族，则UF是X的定向开覆盖.由已知，UF有一个点有限的半开加细V＝{Vσ｜σ∈[Λ]＜ω}，合于σ∈[Λ]＜ω有Vσ⊂∪α∈σUα.

是U的一个点有限的半开加细.

事实上，任意的σ∈[Λ]＜ω，α∈σ，因为Vσ∩Uα⊂Uα，并且

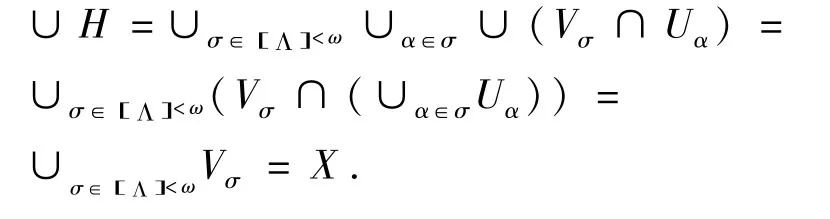
所以，H是X的一个覆盖.又因为Vσ，Uα都是半开集，由上面引理5，Vσ∩Uα是一个半开集，从而H是U的半开加细.

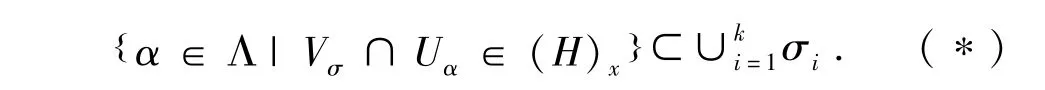
事实上，对于任意的α∈Λ且Vσ∩Uα∈(H)x，则x∈Vσ∩Uα且α∈σ，因为x∈Vσ故存在i0(1≤i0≤k)有σ＝σi0，所以，α∈σ＝σi0⊂∪ki＝1σi.从而，(*)式得证.

(必要性)由定义可直接得到.□

再者，对于S-仿紧空间，具有完备映射下逆保持的性质，同样，在S-亚紧空间中也得到了类似的性质如下:

定理2 设X，Y是两个拓扑空间，f:X→Y是完备(perfect)的优柔映射.如果Y是S-亚紧的，则X也是S-亚紧的.(即在完备映射下S-亚紧是逆保持的)

证明 设U为X的任一定向开覆盖，由已知，任意的y∈Y，有f－1(y)是X的紧子集，从而f－1(y)⊂X＝∪U，所以，存在又因为U是定向的，所以，

即，存在U∈U使得f－1(y)⊂U.

由文献[5]中的定理[Theorem 1.4.13]，存在开集Vy∈U(y)，使得f－1(Vy)⊂U，再由Y的S-亚紧性，Y的开覆盖

事实上，任意的x∈X，记y＝f(x)∈Y，因为W是点有限的，有Δ＝{t∈T｜y∈Wt}为非空有限集，又因为y∈Wt，则x∈f－1(y)⊂f－1(Wt)，并且

因此，{t∈T｜x∈f－1(Wt)}是非空有限集.从而，H是点有限的.

此外，对于任意的t∈T，因为W是{Vy｜y∈Y}的加细，则存在yt∈Y，有Wt⊂Vyt.由Vyt的取法，存在U∈U使得f－1(Vyt)⊂U，故f－1(Wt)⊂f－1(Vyt)⊂U.即W是U的部分加细.又因为∪H，从而W是U的一个加细.

由于f:X→Y是优柔映射，所以，f－1(Wt)为X中的半开集。

从而，U有一个点有限的半开加细H＝{f－1(Wt)｜t∈T }.再由定理1可得，X是S-亚紧的.□

另外，在一般拓扑空间中，如仿紧空间、S-仿紧空间中，都有很好的乘积性质，利用上面的定理2，我们可以得到下面乘积性结论是成立的:

推论3 设X是一个S-亚紧空间，如果Y是紧空间，则X×Y也是S-亚紧空间.

证明设PX:X×Y→X是投影映射，因为，投影映射是连续映射，再由定理2，所以下面只需证明:投影映射PX是一个完备的优柔映射.

事实上，对于任意的A∈SO(X)，存在X中的开集G，使得G⊂A⊂，则

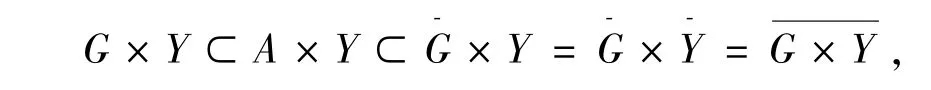
即，存在X×Y中的开集O＝G×Y，使得θ⊂Px－1(A)＝A×Y⊂.因此，

再由文献[5]中的定理[Theorem 3.7.1]，PX还是一个完备映射.

所以，PX:X×Y→X是一个完备优柔映射.由定理2 X×Y是一个S-亚紧空间.□

进一步地，为了得到后面的结果定理5，先给出如下引理:

引理4 Y是拓扑空间X的开子空间，A是Y的半开集，当且仅当存在X中的半开集A′，使得A＝A′∩Y[16].

定理5 设X是一个S-亚紧空间，Y是X的开子空间且Y是半闭集，则Y是一个S-亚紧空间.

证明 设V＝{Vλ｜λ∈Λ}是X的子空间Y的定向开覆盖，由于存在X的半开集族U＝{Uλ｜λ∈Λ}，使得Vλ＝Y∩Uλ(由引理5的必要性可得)，又由于Y是半闭集，故X－Y及U＝{Uλ｜λ∈Λ}组成X的半开覆盖。既然X是一个S-亚紧空间，则存在一个点有限的半开加细W＝{Wt｜t∈Γ}.于是，{Y∩Wt｜t∈Γ}是{Vλ｜λ∈Λ}的Y的点有限半开加细(由引理5的充分性可得)。再由定理1，所以，Y是一个S-亚紧空间。□

强(次强)连续、强(次强)半开、强(次强)同胚映射的概念见文献[17].

定理6 设f是S-亚紧空间X到拓扑空间Y上的一一的、半连续、次强半开的映射，则Y为S-亚紧空间.

证明 设B为Y的任意的定向开复盖，对于B∈B，由f是半连续的，f－1(B)为X中的半开集，则A＝{f－1(B)｜B∈B}是X的开复盖。于是存在A1为X的点有限的半开复盖，且为A的加细。令B1＝{f(A)｜A∈A1}.因f为半开的，f(A)为Y中的半开集，下证{f(A)｜A∈A1}为Y中的点有限族。∀y∈Y，因f是X到拓扑空间Y上的映射，∃x∈X，使f(x)＝y，由A1为点有限族，故存在包含x的开集U与A1中至多有限个元素相交，对于A∈A1，如果A∩U＝∅，由于f为一一的，f(A)∩f(U)＝f(A∩U)＝∅。再因f为开的，所以，在Y中有包含f(x)的开集f(U)至多与{f(A)｜A∈A1}中有限个元素相交.这样，B1＝{f(A)｜A∈A1}为Y的点有限的半开复盖，且为B的加细。故Y为S-亚紧空间。□

由于次强连续映射是半连续的，不难得到如下结果:

推论7 S-亚紧性是次强同胚映射下的不变性质.

[1]LEVINE N.Semi-open sets and Semi-continuing in topological Spaces [J].Amer Math Monthly，1963，70:36-41.

[2]Al-ZOUBI K Y.S-paracompact spaces[J].Acta Math Hunger，2006，110:165-174.

[3]张焰杰，吴昭鑫，杨思鑫.S-亚紧空间[J].四川理工学院学报(自然科学版)，2014，27(1):98-100.

[4]蒋继光.一般拓扑专题选讲[M].成都:四川教育出版社，1991:70-82.

[5]ENGEKING R.General Topology[M].Polish scientific publisher:Warszawa，1977.

[6]CROSSELY S G，HILDEBRAND S K.Semi-topological properties[J]. Fund Math，1972，74:233-254.

[7]朱培勇，雷银彬.拓扑学导论[M].北京:科学出版社，2009:44-45.

[8]LI P Y，SONG Y K.Some remarks on S-paracompact spaces[J].Acta Math Hunger，2008，118(4):345-355.

[9]WANG G W.On layer L-topological spaces[J].Fuzzy System and Mathematics，2008，22(5):37-42.

[10]Al-ZOUBI K Y.S-expandable spaces[J].Acta Math Hunger，2004， 102:203-212.

[11]NJASTAD O.ON some classes of nearly open sets[J].Pacific J Math，1965，15:961-970.

[12]TANAKA H.Submetacompactness incountable products[J].Topology Proc，2003，37(1):307-316.

[13]程吉树，陈水利.点集拓扑学[M].北京:科学出版社，2008:117-128.

[14]梁基华，蒋继光.拓扑学基础[M].北京:高等教育出版社，2005.

[15]ENDERTON H B.Element of Set Theory[M].New York:Acadamic Press，1997.

[16]林诗丽.拓扑空间的半分离性及C-空间[J].华南师范大学学报(数学专刊)，1984:89-93.

[17]胡庆平.关于分离性和同胚关系的一些推广[J].数学研究与评论，1984(2):13-117.

(责任编辑:付强，张阳，李建忠，罗敏；英文编辑:周序林)

Some results on the S-metacompact space

PENG Zhi-nan，ZHU Pei-yong
(School of Mathematical Sciences，UESTC，Chengdu 611731，P.R.C.)

Some properties of the S-metacompact space are studied.The results are obtained as follows:(1)The topological space X is S-metacompact，if and only if each directed open cover of X has a point finite semi-open refinement.(2)Suppose that X，Y are topological space，f:X➝Y is perfect irresolute mapping，if Y is S-metacompact，such that X is S-matecompact.(3)Suppose Y is an S-matecompact space，if Y is a compact space，then X×Y is also an S-matecompact space.

S-matacompact space；perfect mapping；irresolute mapping；directed open cover；point finite semi-open refinement

O189

A

2095-4271(2016)06-0692-04

10.11920/xnmdzk.2016.06.017

2015-10-19

彭知南(1991-)，男，汉族，硕士研究生.Email:pengzhinan5872＠163.com.

朱培勇(1956-)，男，四川自贡人，教授，博导.研究方向:拓扑学与混沌理论研究.

国家自然科学基金资助(11501391)