GF-空间上Nash平衡的存在性结果

计 伟，张珺铭

(贵州建设职业技术学院，贵州 贵阳 551400)

GF-空间上Nash平衡的存在性结果

计 伟，张珺铭

(贵州建设职业技术学院，贵州 贵阳 551400)

在抽象凸空间中，给出GF-空间和强Fan-Browder不动点性质的定义，并且在GF-空间中，应用抽象函数代替实值函数作为博弈支付函数，构造GF-空间中博弈模型，应用强Fan-Browder不动点性质证明GF-空间上博弈模型Nash均衡点的存在性.同时也证明了在度量空间和紧拓扑空间上的闭值KKM映射具有有限交性质.

GF－空间；Nash平衡点；不动点性质；博弈模型

1944年，von Neumann和Morgenstern合作出版了《博弈论与经济行为》一书，宣告博弈论正式诞生. 1950年，Nash应用集值映射的Kakutani不动点定理证明了n人博弈均衡点的存在性，1951年，他又应用连续映射的Brouwer不动点定理证明了非合作博弈均衡点的存在性.之后，博弈论的研究非常活跃，取得了许多重要成果，并且先后在1994年、1996年、2001年、2005年、2007年和2012年的Nobel经济学奖授予了从事博弈论研究和应用的学者.可以说，博弈思想与方法的应用广泛而深刻，因为它抽象地分析了利益冲突问题，而且成为经济学、人文科学、社会科学普遍认可的、充满生机活力的工具和语言，同时也展示了数学与经济学、人文科学、社会科学的交叉与融合[1－7].

1 预备知识

首先，介绍如下引理.

引理1.1 设Y为线性拓扑空间中的某一列紧凸子集，Δn＝e0e1…en为一标准单纯型，p:Y→Δn为连续的单纯型映射，F:Δn→2Y上半连续且非空闭凸值，则p°F:Δn→2Δn存在不动点.

定义1.1 设Y为拓扑空间，Δn＝e0e1…en为一标准单纯型，F:Δn→2Y，如果对每一连续的单纯型映射p:Y→Δn，:Δn→2Δn在单纯型Δn中具有不动点，则称F关于单纯型映射具有不动点性质.

由引理1.1及定义1.1，若Y为线性拓扑空间中的某一列紧凸子集，则任意上半连续、非空闭凸值映射F:Δn→2Y关于任一单纯型映射具有不动点性质.

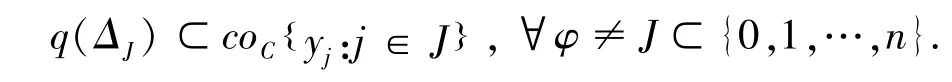
则称(Y，C)为GF－空间.

由引理1.1及定义1.2，可推出如下结论[8－12].

命题1.1 若Y为赋范空间的某一紧凸子集，C为Y上的某一抽象凸结构，q:Δn→2Y上半连续、非空闭凸值，且满足:

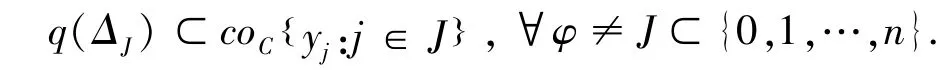
则(Y，C)为GF－空间.

定义1.3 设(Y，C)为抽象凸空间且Y为拓扑空间，称Y具有Fan－Browder不动点性质，如果对任意的非空凸值且开逆值的映射F:Y→2Y，F在Y中存在不动点.

定义1.4 设X是一个Hausdorff拓扑向量空间，C是X中的非空子集，如果对任意的x∈C，对任意的λ＞0，都有λx∈C，则称C是X中的一个锥，此时必有λC＝C.如果锥C是闭集，则称C是闭锥，此时必有0∈C.如果锥C是凸集，则称C是凸锥，此时必有C＋C＝C.如果C是锥，且对任意的x∈C{0}，必有－x∉C，则称C是尖锥.

定义1.5 设X，Y是两个拓扑空间，K是X中的一个非空子集，集值映射F:K→P0(Y)，x∈K，若对任何Y中的开邻域G，满足G⊃F(x)，都存在x在X中的开邻域O(x)，使得对任意的x'∈O(x)都有F(x')⊂G，则称F在x处是上半连续的，如果F在K上每一点均是上半连续的，则称F在K上是上半连续的；若对任何Y中的开邻域G，满足G∩F(x)≠∅，都存在x在X中的开邻域O(x)，使得对任意的x'∈O(x)都有F(x')∩G≠∅，则称F在x处是下半连续的；如果F在K上每一点均是下半连续的，则称F在K上是下半连续；

若F在x处既上半连续又下半连续，则称F在x处是连续的，如果F在K上每一点均是连续的，则称F在K上是连续的[13－15].

2 主要结论

定理2.1 设(Y，C)为GF－空间，Y为度量空间，F:Y→2Y为一闭值的KKM映射，则{F(y):y∈Y}具有有限交性质.

证明:用反证法.设F:Y→2Y为一闭值的KKM映射，若{F(y):y∈Y}不具有有限交性质，则存在某一有限集于是作单位分解如下:

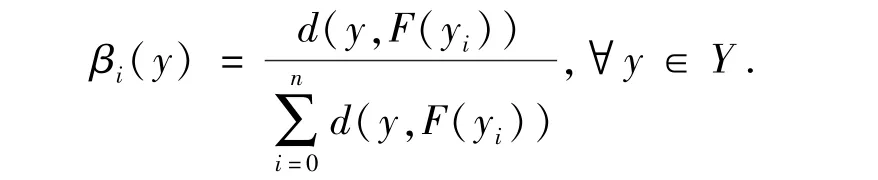
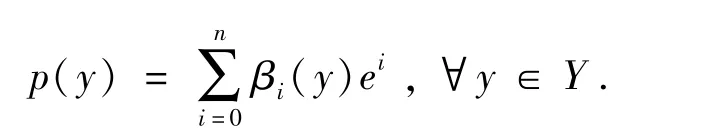
由(Y，C)为GF－空间，于是存在q:Δn→2Y关于单纯型映射具有不动点性质，且满足:

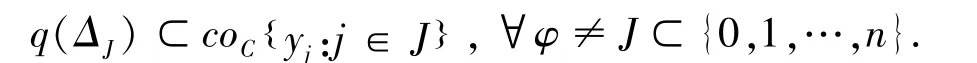
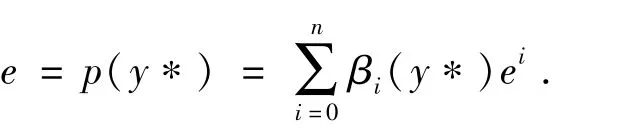
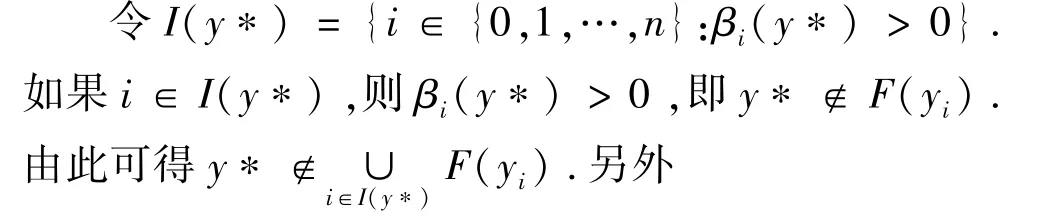
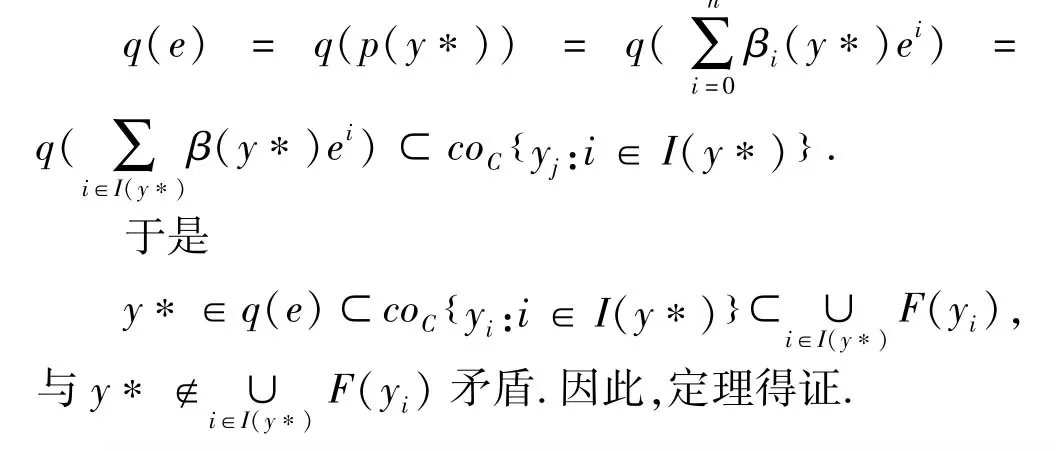
因为紧空间的开覆盖一定存在单位分解，因此定理2.1中Y为度量空间，也可以改为紧拓扑空间，即有下述结果.

定理2.2 设(Y，C)为GF－空间，Y为紧拓扑空间，F:Y→2Y为一闭值的KKM映射，则{F(y):y∈Y}具有有限交性质.

定义2.3 设(Y，C)为抽象凸空间且Y为拓扑空间，称Y具有强Fan－Browder不动点性质，如果对任意的非空弱凸值且开逆值的映射F:Y→2Y，F在Y中存在不动点.

由定理2.2，可得如下结论.

定理2.3 设(Y，C)为GF－空间，且Y为紧拓扑空间，则Y具有具有强Fan－Browder不动点性质.

下面给出引理2.1的一个推广结果(参见文献[10]引理2.9.3).

引理2.2 设Y为紧拓扑空间，Δn＝e0e1…en为一标准单纯型，p:Y→2Δn连续的单纯型映射，F:Δn→2Y上半连续且非空紧可缩值的(即对每一y∈Y，F(y)是一紧可缩的集合)，则p°F:Δn→2Δn存在不动点.

由引理2.2及定义2.2，可推出如下结论.

命题2.2 设(Y，C)为抽象凸空间且Y为紧拓扑空间，对每个有限集e0e1…en为一标准单纯型，若存在q:Δn→2Y上半连续、非空闭凸值，且满足:

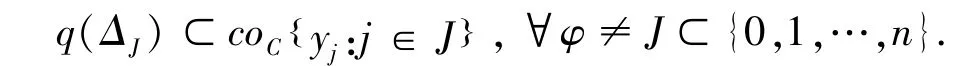
则(Y，C)为GF－空间.

为了方便讨论，我们把满足上述条件的GF－空间定义为GF0-空间.

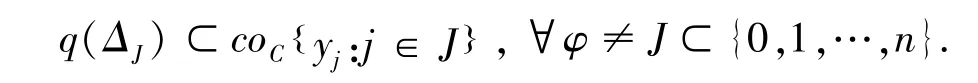
则称(Y，C)为GF0－空间.

对于抽象凸空间来说，下述命题及其证明将说明上半连续集值映射比较容易构造.

命题2.3 设(Y，C)是一个抽象凸空间，对每一个有限集标准单纯型，定义q:Δn→2Y如下:

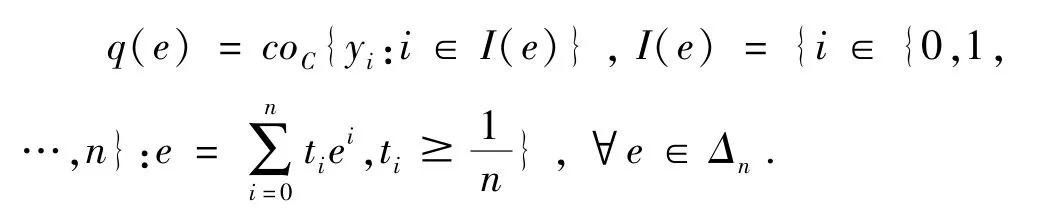
则q:Δn→2Y上半连续、非空凸值，且满足:

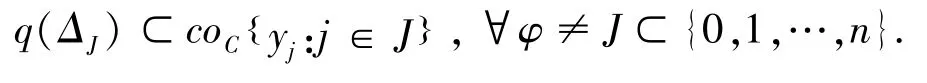
下面考虑如下博弈模型:

设E为Hausdorff拓扑向量空间，C为E中某一个闭凸尖锥.

(1)设N＝{1，2，…，n}为局中人集合；

(2)对任意⊆，局中人i的策略集为Xi，×为策略组合空间，其中(Xi，C)、(X，C)为GF－空间；

(3)对局中人X，定义向量值支付函数为映射fi:

则称x*∈x为博弈Γ的Nash平衡点.

下面给出GF－空间中Nash平衡的存在性结果.

定理2.4 设博弈为Γ＝{N；X；E，C；f1，f2，…，fn}，且满足:

(1)对任意的i∈N，Xi是紧GF－凸集；

(2)对任意的i∈N，fi在X上上半连续；

(3)对任意的i∈N，对任意xi∈Xi，fi(xi，x－i)在X－i上是下半连续的；

(4)对任意的i∈N，对任意x－i∈X－i，xi→fi(xi，x－i)在Xi上是GF－拟凹.

则:博弈Γ存在Nash平衡点.

[1]NEUMANN J VON，MORGENSTERN.博弈论与经济行为[M].王文玉，译.北京:生活·读书·新知三联书店，2004.

[2]NATH J.Equilibrium points in N-person games[J].proceedings of the National Academic of Sciences，USA，1950，36:48-49.

[3]NATH J.Non cooperative Games[J].Annals of Math，1951，54:286-295.

[4]俞建.博弈论与非线性分析续论[M].北京:科学出版社，2011.

[5]俞建.博弈论选讲[M].北京:科学出版社，2014.

[6]BLACKWELL D.An Analog of the Minimax Theorem for Vector payoffs [J].Pac J Math，1956，6:1-8.

[7]XIANG S W，Yang H，Some properties of abstract convexity structures on topological spaces[J].Nonlinear Analysis，2007，67:803-808.

[8]XIANG S W，XIA S Y，CHEN J.KKM lemmas and minimax inequality theorems in abstract convexity spaces[J].Fixed point theory and application，2013，209(12):19-21.

[9]JIA W S，XIANG S W，HE J H，et al.Existence and stability of weakly Pareto-Nash equilibrium for generalized multiobjective multi-leader–follower games[J].Journal of Global Optimization，2015，61(2):19-22.

[10]YUAN X Z.KKM Theory and Application in Nonlinear Analysis[M]. New York:Marcel Dekker Inc，1999.

[11]俞建，袁先智.樊畿不等式及其在博弈论中的应用[J].应用数学与计算数学学报，2015，1:59-68.

[12]PARK S.A genesis of general KKM theorems for abstract convex spaces[J].J Nonlinear Anal Optim，2011，2(1):121-132.

[13]计伟，不具支付函数的博弈平衡研究[D].贵阳:贵州大学，2012.

[14]SULIMAN AL-HOMIDAN，QAMRUL HASAN ANSARI.fixd point theorems on product topological semilattice spaces，generalized abstract economies and systems of generalized vector quasi-equilibrum problems [J].Taiwanese joural of mathematics，1996，25:291-306.

[15]俞建.博弈论与非线性分析[M].北京:科学出版社，2008.

(责任编辑:付强，张阳，李建忠，罗敏；英文编辑:周序林)

Result of Nash equilibrium existence in GF-space

JI Wei，ZHANG Jun-ming
(Guizhou Polytechnic of Construction，Guiyang 551400，P.R.C.)

In the abstract convex space，the definitions of GF－space and property of strong Fan-Browder fixed point are given. And in GF－space，real value function is used，instead of abstract function，as game pay function to construct game model in GF space.The property of Strong Fan-Browder fixed point is used to prove the existence of Nash Equilibrium Point of game model in GF-Space and the property of finite commutation of the closed KKM mapping is proved in metric space and compact space.

GF－space；Nash equilibrium；property of fixed point；game model

O225

A

2095-4271(2016)06-0688-04

10.11920/xnmdzk.2016.06.016

2016-04-17

计伟(1984-)，男，汉族，贵州遵义人，助教.研究方向:博弈论与非线性分析、最优化理论与方法研究.E-mail:jiwei10000＠126.com