基于相似比的变邻域搜索的快速分形编码算法

汪明华，李高平

(西南民族大学计算机科学与技术学院，四川 成都 610041)

基于相似比的变邻域搜索的快速分形编码算法

汪明华，李高平

(西南民族大学计算机科学与技术学院，四川 成都 610041)

为了解决基本分形图像编码算法中的编码过程特别耗时问题，通过定义每个range块和domain块的相似比，建立它与匹配均方根误差间的关系不等式，可把寻找range块的最佳匹配domain块的全局搜索变为近邻搜索.鉴于在自仿射变换下最优匹配块间的相似比值应该接近，但它们间的远近程度不一致，因此，每个range块的最优匹配块搜索范围应限制在与其相似比值接近的domain块变邻域内.四幅图像的仿真结果表明，它确实能够在PSNR降低0.103dB(其结构相似性SSIM值仅下降0.0004)的情况下，平均耗时仅为基本分形编码算法的38.97%左右，而且也优于可选特征算法，实现了加快编码过程速度的目标.

图像压缩；分形图像编码；变邻域搜索；相似比

随着信息技术和媒体技术的飞速发展，如何有效处理海量信息中的图像数据，已经成为人们关注的热点问题，各种图像压缩编码方法应运而生.基于图像内部的自相似性来实现图像数据压缩的分形编码方法被认为是目前最有前途的编码技术之一，但是因其编码时间长、计算复杂性高等问题使其应用性受到了限制.近年来，在如何保证图像质量的前提下来加快分形编码过程的速度，已成为许多学者研究的关键问题，通过提出的措施也取得了较好的加速效果[1-17].在文献[10]中提出了一种基于相似比的分形编码算法并给出了可行性分析，在编码过程中，每个range块只搜索与range块相似比相差较近的码书中的domain块，通过减少搜索对象来达到缩减最佳匹配过程的过度耗时问题.本文对此做了进一步研究，不仅从理论上证明匹配均方误差与匹配块相似比间的关系不等式，而且据此提出了变邻域搜索的快速分形编码算法.仿真实验结果表明，在编码过程的匹配阶段，基于相似比为依据所做的近邻搜索来取代全局搜索，可以获取大部分待编码range块的最优匹配块，且它优于可选特征[16]，据此提出的变邻域搜索快速算法，在解码图像质量降低约0.103dB(其结构相似性SSIM值仅下降约0.0004)的情况下，编码过程耗时仅为基本分形图像编码算法的38.97%，减少编码时间约61%.

1 基本分形图像编码算法

首先选取一种分割方式，将图像分成两类子块集:编码range块(简称R块，大小为n×n，互不重叠)集和domain块集(简称D块，大小为2n×2n，允许重叠).搜索所用码书Ω，是将domain块集中每个D块采用4－邻域像素值平均收缩成n×n的子块，再经过8个等距变换而得到.

对每个待编码R块，需要求解下面的极小化问题(1)寻找其最优匹配D块的位置和自仿射变换w.

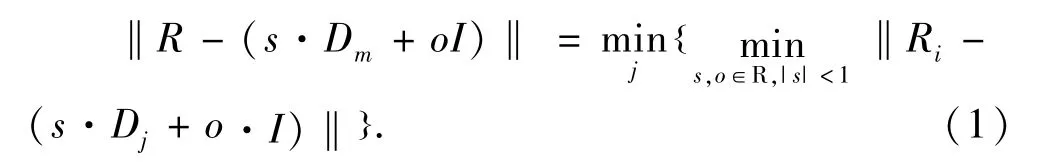
其中，m表示R块的最优匹配块序号，I∈Rn×n是所有元素均为1的常值块，R＝(r1，…，rk，…，rM)、D＝(d1，…，dk，…，dM)(M＝n×n)分别表示R块、D块像素点灰度值按某种方式向量化后的向量.

鉴于式(1)是NP难问题，故只能求次优解.首先忽略式(1)中约束｜s｜＜1，将(1)的内层约束极小化转化为(2)式的极小值问题来求解:

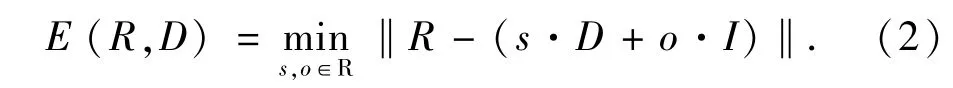
然后对不满足｜s｜＜1的对比度因子s以截断方式处理.式(1)的外层极小化问题用全搜索法求解:

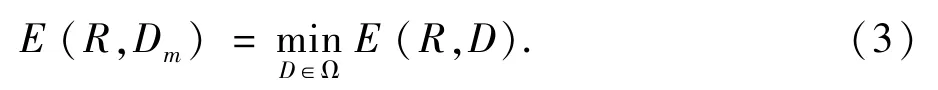
解码图像用分形码按迭代方式重构.

2 变邻域搜索的快速分形编码算法

2.1 算法的理论分析

在基本分形算法的匹配搜索阶段，每个range块都以全搜索方式在整个码书Ω(其容量庞大)中寻找它的最优匹配domain块，而导致匹配搜索需要特别多的时间.下面首先定义图像块的相似比，从理论上证明匹配均方误差与匹配块相似比间的关系不等式，然后据此提出变邻域搜索的快速分形编码算法，以缩减匹配搜索所需时间.

定义 图像块上像素灰度值按行向量后记为X＝(x1，…，xi，…，xM)∈RM(RM代表n×n＝M灰度图像块空间)，相应地，它的上半部分子块记为X*＝，定义图像块的相似比为去均值后的2-范数‖X*－·I‖，与X去均值后的2-范数‖X－·I‖之比[10]，即

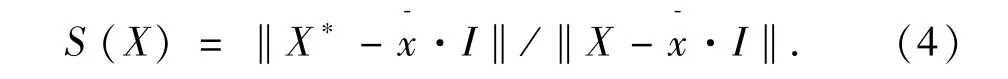
在自仿射变换下，R块能与D块组成最优匹配块时，它们间的相似比应该比较接近[10]，即

下面的定理进一步给出R块与D块的匹配误差与其相似比间的关系，它们共同构成本文算法的理论基础.

定理 若图像块大小为n×n，其上的像素灰度值按升序向量化为R，D∈RM(M＝n×n)，则有下面的不等式:

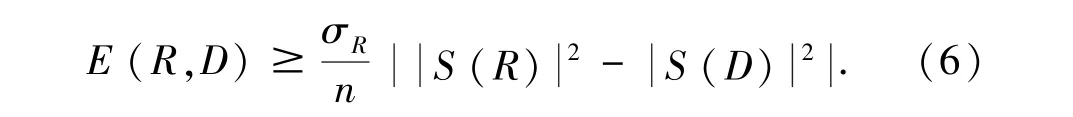
由2-范数、内积以及式(4)有

由Cauchy-Schwarz不等式和式(7)有

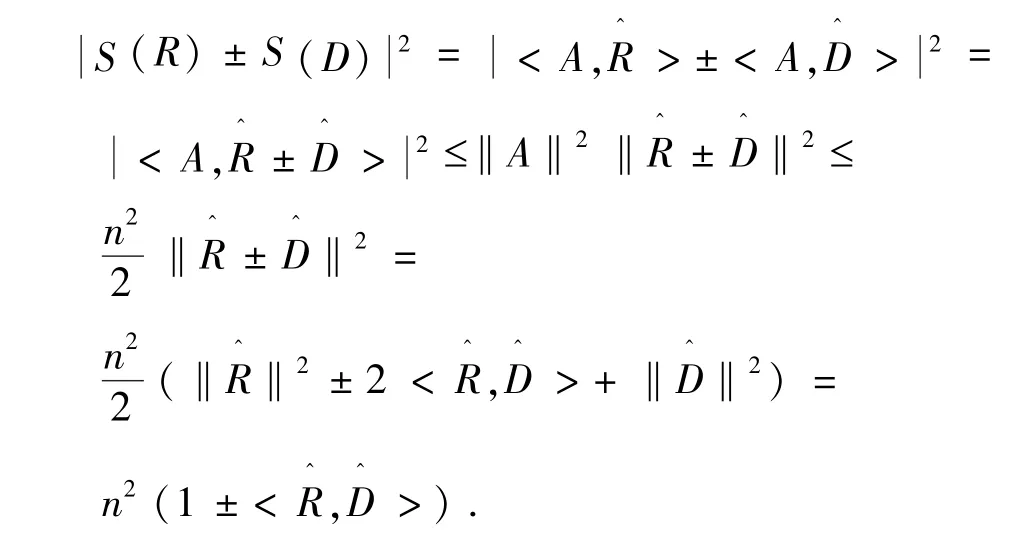
又问题(2)的解为

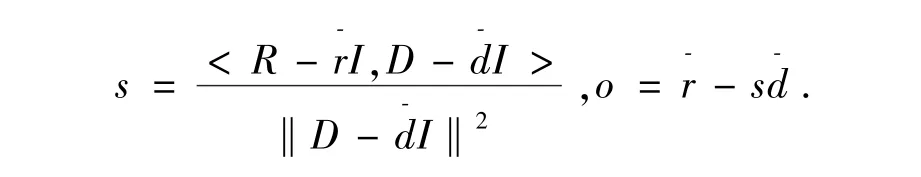
故匹配均方误差为

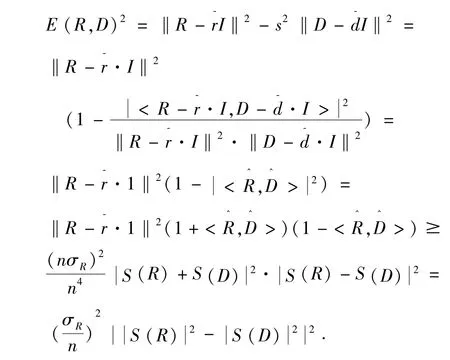
定理得证.

2.2 快速编码算法设计

基本分形编码算法中匹配搜索阶段的耗时主要取决于需要编码的R块数量、码书Ω容量.比如说，对于一个N×N大小的图像I，若编码R块和D块大小分别设为n×n和2n×2n，则需要编码的R块数量为NR＝(N/n)2，码书Ω容量为((N－2n)/δ＋1)2(δ为码书步长)，以全搜索方式寻找每个R块的最优匹配D块，那就需要NRD＝次匹配.问题在于，是不是每个R块都需要NRD次匹配搜索才能找到它的最优匹配D块?在式(4)定义的相似比下，从自仿射变换角度看，R块能与D块组成最优匹配对的条件是它们间的相似比应该比较接近；从R块与D块的匹配误差角度看，式(6)表明，R块和D块能组成匹配对的必要条件是R块的相似比S(R)应要求与D块相似比S(D)接近.这些都说明在相似比意义下应该是近邻，也就是说，每个编码不一定需要搜索完整个码书Ω来找它的最优匹配D块.下一个问题是，如何确定每个R块的搜索码书Ωs?并要求这个码书的容量尽可能小，且包含R块的最优匹配D块.根据上面分析得出的近邻结论，在设计快速算法时，首先确定邻域中心码本块D0，将码书中的全体D块按相似比值大小进行升序排列，即S(Di)≤S(Di＋1)，然后，在升序码书Ω中采用二分法搜索与编码R块相似比值S(R)相差最小的D块为D0，即

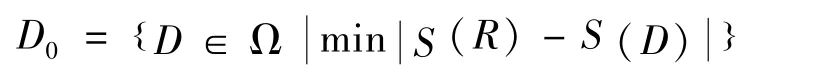
然后，对每个编码的R块，它的搜索码书Ωs就在D0的k邻域内进行，即

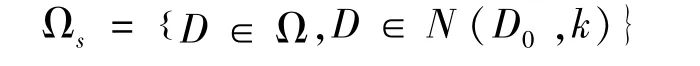
值得说明的是，要使Ωs中包含R块的最优匹配D块，每个编码R块的邻域半径k的大小是不同的(仿真实验给予验证).显然，将k设定为一个较小的固定值，那在Ωs中找不到它的最优匹配D块的可能性就会很大，解码图像质量会变得很差，若k设定为一个较大的固定值，就不能达到缩减匹配搜索耗时目的.为了解决这个难题，设计一个变邻域搜索方案:根据解码图像质量要求高低，设定匹配误差E(R，D)阈值为λ，先取k＝K0(K0为初始邻域半径)，看编码R块能否在邻域N(D0，k)中找到E(R，D)≤λ的D块，若不能，就取k＝K0＋K(K为扩域步长)，再在邻域N(D0，k)中找能否满足E(R，D)≤λ的D块，若还不能，就再取k＝K0＋2K，…，k＝K0＋nK(n为扩域次数)，直至在邻域N(D0，k)中找到满足要求的D块为止.然后将其位置序号m、所得量化参数，及等距变换的序号t作为该R块的分形码(m，，，t).所有编码R块的分形码集合就构成编码图像的分形码.

3 仿真实验结果

本节的仿真实验验证两个主要问题:一是在相似比意义下，编码R块与它的最优匹配D块是否为近邻?二是变邻域搜索快速编码算法的有效性.为此，选择4幅复杂性各异的图像Lena、Peppers、Boat、Baboon(512×512，8bit量化)为测试对象，方块分割图像，R块、D块及码书步长分别取为4×4、8×8和8，此时，编码R块集数量为16384，码书Ω容量为32768，仿真实验平台为PC机(AMD Athlon，3.01GH CPU/2G内存)，算法用C＋＋编写的程序实现.

3.1 相似比意义下的近邻验证

本文通过定义图像块的相似比来刻画蕴含在图像块中的信息.下面通过仿真实验测出编码R块在全搜索中得到的最优匹配块，在相似比意义下的邻域中心码本块D0的k邻域N(D0，k)内的分布情况，4幅测试图像的结果列于表1，表中标识“M-N”表示邻域半径k的取值区间为

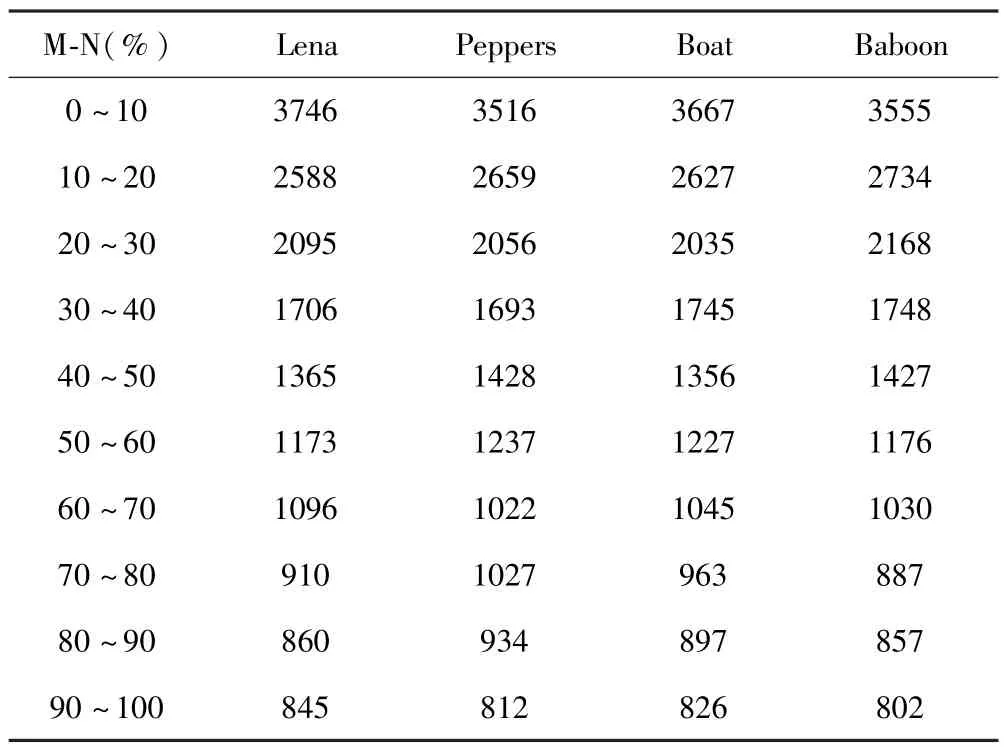
表1 最优匹配块落入邻域N(D0，k)内的R块数量Table 1 Quantity of the range block of the best-matched domain block fall into neighbor N(D0，k)

表1数据显示，从4幅测试图像的平均值看，只需搜索码书的10%空间，就有大约22%的编码R块能找到它的最优匹配块，搜索50%空间能找到的比例为70%多，编码R块要搜索完整个码书才能找到最佳匹配块的比例仅为5%.这表明大多数的编码R块的最优匹配D块就在图像块相似比意义下，位于邻域中心码本块D0附近，当然远近是不一样的，佐证了快速算法的理论基础.

下面来比较图像块的相似比与可选特征[16]，谁能更好刻画图像块的信息?取4幅测试图像分别在相似比意义和可选特征意义下，在邻域N(D0，k)中能找到最优匹配块的编码R块数量比例来进行比较，结果列于表2(数据是4幅测试图像的平均值)，表中记号P10、P50和P100分别表示能在邻域半径k≤100%时，找到的最优匹配块的编码R块数量占总编码R块数的比例(用百分数表示).

表2 最优匹配块落入邻域N(D0，k)内的R块比例Table 2 Proportion of the range block of the best-matched domain block fall into neighbor N(D0，k)

表2中数据表明，从所给三项指标看，图像块的相似比优于可选特征，能更好刻画图像块的信息.

3.2 变邻域搜索快速编码算法的有效性验证

在3.2节设计的变邻域搜索快速编码算法，涉及匹配误差E(R，D)阈值λ，初始邻域半径K0，扩域步长K.经实验验证，初始邻域半径K0和扩域步长K对算法结果影响很小，取K0＝1，K＝2，在此主要来确定对算法结果影响很大的阈值λ，4幅测试图像的解码图像质量随λ的变化情况如图1所示.

从图1可以看出，随着匹配误差阈值λ的增大，测试图像的解码图像质量(以PSNR度量)是在降低，降低速率大小取决于需编码图像中所含细节多少，所以，匹配误差阈值λ最好根据实际情况对解码图像质量要求高低进行选取.对所给4幅测试图像的情况，当λ≤10时，以PSNR度量的解码图像质量降低很少，故取λ＝10.

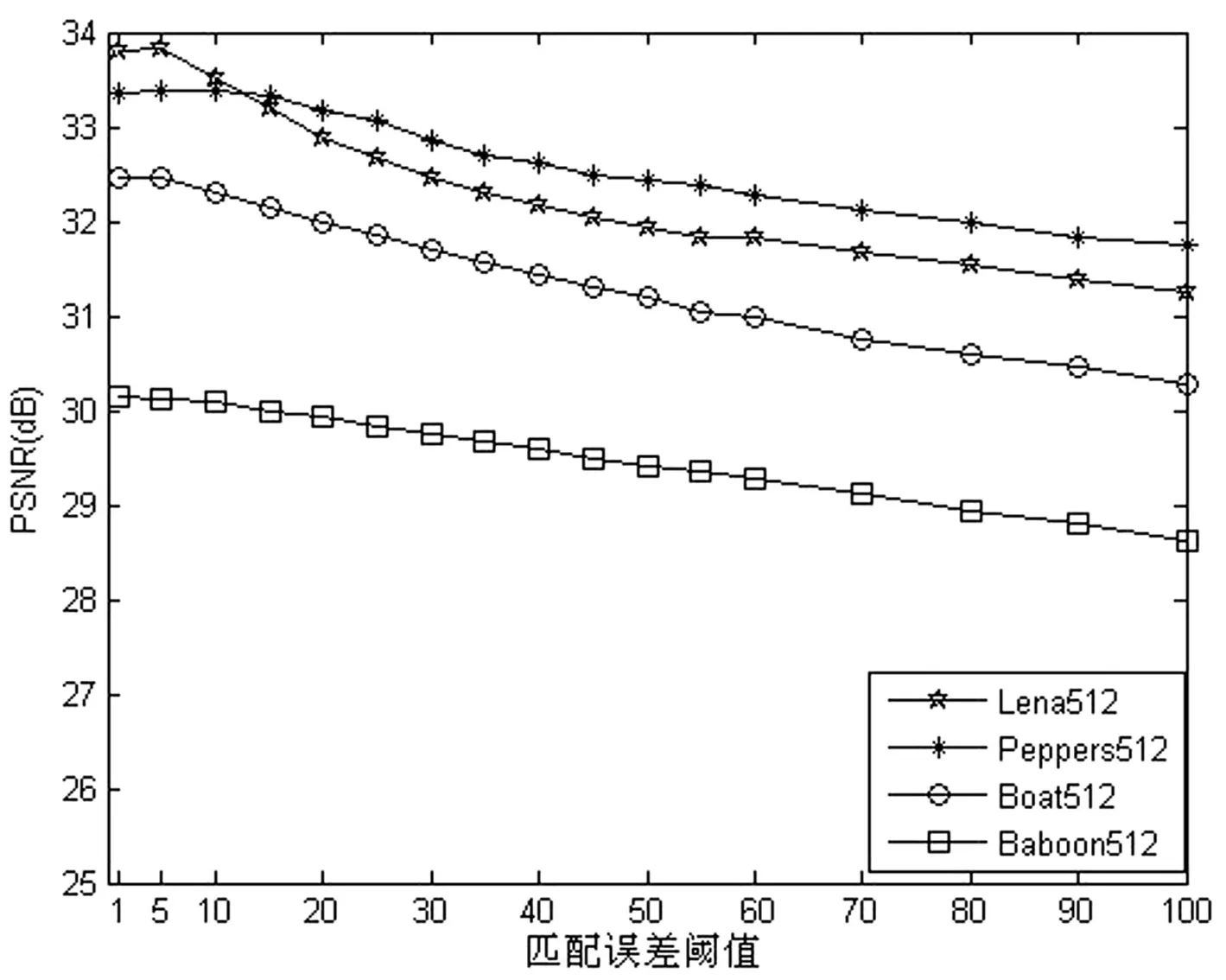
图1 解码图像质量随匹配误差阈值λ的变化情况Fig.1 The quality of the decoded image vs.matching error threshold λ

为验证变邻域搜索快速编码算法的有效性.选编码时间(秒)、峰值信噪比PSNR(dB)和结构相似性SSIM(structural similarity)为测试性能参数，本文算法(K0＝1，K＝2，λ＝10)与基本算法的对比实验结果列于表3.

表3 本文算法与基本分形算法对比结果Table 3 The comparison between the proposed algorithm and the basic fractal algorithm

分析表3数据，取4幅测试图像的平均值，本文所提算法在编码过程中所耗时间仅为基本算法的38.97%，减少了约61%的时间，以PSNR度量的解码图像质量降低约0.103dB，以SSIM度量的解码图像质量降低约0.0004(表明解码图像与其编码前的图像相比，图像中的对象结构属性几乎没有变化，也说明它的主观质量是很不错的).这充分例证了变邻域搜索快速编码算法是有效的.在此需要说明的是，表3显示有些图像在本文算法下的解码图像质量高于基本算法，原因在于两种算法都是有损算法，解码图像质量依赖于对不满足约束｜s｜＜1的对比度因子s作截断处理的数目.

4 结论

本文运用图像块的相似比，从理论上证明了能组成匹配对的R块与D块，它们的相似比应该是接近的，并给予了实验佐证.在此基础上，把消费时间最多的R块与码书Ω中D块的匹配全搜索问题转化为邻域中心码本块D0(其相似比值与S(R)最接近)的邻域搜索问题，以缩减搜索空间.考虑到不同编码R块需要搜索的邻域半径k是不一样的，本文提出了变邻域搜索的快速分形编码算法，在解码图像质量(以PSNR度量)降低0.103dB(以SSIM值度量仅下降约0.0004)的情况下，编码过程所需时间仅为基本算法耗时的38.97%左右，达到了保质(或少降质)提速目的，它无疑为加快基本分形图像编码过程提供了一个候选算法.

[1]AIHUA ZHANG，PEIYANG.An Improved Algorithm for Fractal Image Encoding Based on Relative Error[C].IEEE:5th International Congress on Image and Signal Processing，2012:254-25.

[2]TANG GUOWEI，WU SHUANG ZHANG YAN.An Improved Fast Fractal Image Coding Algorithm[C].IEEE:2th International Conference on Computer Science and Network Technology，2012:730-732.

[3]FENGXIA YANG.Study on the Effective Measures of Enhancing the Fractal Image Coding[C].International Conference on Computational and Information Sciences，CPS，2013:160-162.

[4]JIANJI WANG，XUGUANG LAN，YUEHU LIU et al.Fractal image encoding with flexible classification sets[J].Chin Sci Bull，2014，59 (14):1597-1606.

[5]LI LOU，YONG LI.Research of Neighborhood Searching Fractal Image Coding Algorithm based on Ant Colony Optimization[C].IEEE:SAI Intelligent Systems Conference，2015:761-764.

[6]WANG XING YUAN，ZHANG DOU DOU，WEI NA.Fractal image coding algorithm using particle swarm optimisation and hybrid quadtree [J].IET Image process，2015，9(2):153-161.

[7]李高平.三均值特征的快速分形图像编码算法[J].中国图象图形学报，2011，16(1):1-7.

[8]李高平，向慧芬，赵正武.四分位数特征的快速分形图像编码算法[J].计算机工程与应用，2011，47(22):145-148.

[9]宁培兴，黄仁.数理统计特征的快速图像分形压缩算法研究[J].计算机工程与应用，2012，48(31):161-165.

[10]张爱华，盛飞，杨培，等.基于相似比的快速分形编码算法[J].计算机技术与发展，2012，22(11):176-178.

[11]钱雅儒，郭中华，雍慧.一种改进的规范块半范数算法[J].计算机工程，2012，38(2):221-223.

[12]苏兆宝，周敏，郑红婵，等.基于像素采样的分形图像编码算法[J].计算机系统应用，2013，22(12):136-139，167.

[13]杨培.基于分形图像编码的快速搜索方法研究[D].南京:南京邮电大学，2013.

[14]孙媛媛，孔瑞卿.一种基于字典的快速分形图像编码方法[J].计算机工程，2013，39(1):230-233.

[15]刘树群，潘章容.基于Fisher分类和空间映射的分形图像编码方法[J].计算机应用，2013，33(12):3552-3554，3558.

[16]袁宗文，鲁业频，杨汉生.可选特征的快速分形图像编码[J].中国图象图形学报，2015，20(2):0177-0182.

[17]裔传俊，刘亮.采用边缘分类和平均偏差比较的分形图像编码[J].计算机应用与软件，2015，32(2):211-214.

(责任编辑:张阳，付强，李建忠，罗敏；英文编辑:周序林)

Fast fractal encoding algorithm based on similarity ratio and variable neighborhood search

WANG Ming-hua，LI Gao-ping
(School of Computer Science＆Technology，Southwest University for Nationalities，Chengdu 610041，P.R.C.)

This research is to shorten the exhaustive encoding time of the basic fractal image encoding algorithm.The search scope of best-matched block for an input range block is local against full on the basis of an inequality linking the root-meansquare and defining the similarity ratio.In detail，its search space should be the vicinity of the initial-matched block(i.e.，the domain block having the closet similarity ratio to the input range block being encoded)by the self-affine transformation，but the size of search neighborhood is inconsistent.Therefore，the optimal matching search scope of the input range block being encoded should be the variable neighborhood of initial-matched block.Simulation results of four test images show that average time of the proposed scheme is only about 38.97%while there is averagely the PSNR decrease of 0.103dB(its the structural similarity decrease of 0.0004)，in comparison with the basic fractal algorithm.Moreover，it is better than the optional feature algorithm，the proposed algorithm achieves an objective of speeding up the encoding process.

image compression；fractal image coding；variable neighborhood search；similarity ratio

TP391.41

A

2095-4271(2016)06-0682-06

10.11920/xnmdzk.2016.06.015

2016-08-11

李高平(1966－)，男，教授.研究方向:分形理论及其在图像处理中的应用研究.E-mail:pinggaoli＠163.com

四川省应用基础项目(2013JY0180)；2016年度中央高校基本科研业务费专项资金项目(2016ZYXS14)