澄清“角”里的误解

□周伦菊

澄清“角”里的误解

□周伦菊

有些同学在学习角时，由于对基本概念及图形的特征理解不透彻而出现一些错误，现将这些错误归纳如下，希望大家在学习时能引以为戒.

一、概念理解错误

例1下列关于角的说法中，正确的个数有（）.

①两条射线所组成的图形叫做角.②角是有公共端点的两条射线.③角是一条射线从一个位置旋转到另一个位置所组成的图形.④两条射线具有同一个端点时，就组成了一个角.⑤一条直线就是一个平角，射线是一个周角.

A.0个B.1个

C.2个D.3个

错解：D.

错因分析：错解的原因是对角的概念理解不清.①中忽视组成角的两条射线必须有公共点；②中把角与射线两个不同的概念混淆了，忽视角是一种基本图形；③中没有确定是否绕着它的端点旋转到另一个位置；④是正确的.⑤平角和周角也是角，由角的顶点和两条边组成，而直线和射线就不具备这些要素.显然，平角的两边在同一条直线上，但不能据此就说“直线是一个平角”.

正解：B.

点评：角的概念有两种表达方式：①有公共端点的两条射线组成的图形叫做角.它指明了角的构成要素：两条射线作为角的两条边，公共端点作为角的顶点.②角可以看作一条射线绕着它的端点旋转所形成的图形.

二、混淆角的表示方法

例2如图1，以点B为顶点的角有几个？请分别把它们表示出来.

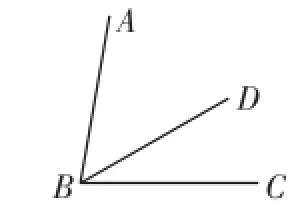
图1

错解：以B为顶点的角有6个，分别是∠B、∠ABD、∠DBC、∠DBA、∠CBD、∠ABC.

错因分析：由于没有掌握角的概念及角的表示方法，把一个角的不同表示重复计数，导致错误.∠ABD与∠DBA，∠DBC与∠CBD，∠ABC与∠CBA分别表示同一个角，“∠B”应改为∠ABC.

正解：图中共有3个角，它们分别是∠ABD、∠DBC、∠ABC.

点评：当一个顶点处有多个角时，哪个角都不能用一个表示顶点的大写字母表示.

三、思考不周导致漏解

例3在平面内，已知射线OA，若从点O引两条射线OB和OC，使∠AOB＝70°，∠BOC＝40°，求∠AOC的度数.

错解：如图2，

∠AOC＝∠AOB＋∠BOC

＝70°＋40°＝110°.

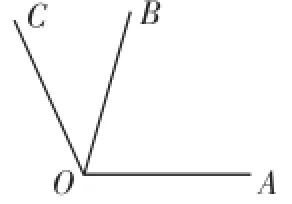
图2

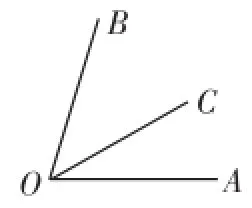
图3

错因分析：本题忽视了OC可能在∠AOB的外部，也可能在其内部，从而造成了漏解.

正解：分两种情况：（1）当OC在∠AOB的外部时，如图2，∠AOC＝∠AOB＋∠BOC＝70°＋40°＝110°；

（2）当OC在∠AOB的内部时，如图3，∠AOC＝∠AOB－∠BOC＝ 70°－40°＝30°.

故∠AOC的度数为110°或30°.

点评：没有指明射线OC在∠AOB的内部还是外部时，一定要注意分类讨论，根据射线OC不同位置求解.

四、识图型错误

例4如图4，已知∠AOC＝∠BOC＝∠DOE＝90°，问图中是否有与∠COD互补的角？

图4

错解：观察图形可知，图中没有与∠COD互补的角.

错因分析：由∠BOC＝90°可知，∠BOE与∠COE互为余角.由∠DOE＝90°可知，∠COE与∠COD互为余角，根据“同角的余角相等”得∠BOE＝∠COD.可见，要找与∠COD互补的角，可转化为找与∠BOE互补的角.观察图形知，∠BOE与∠AOE互为补角，因此与∠COD互补的角是∠AOE.

正解：图中有与∠COD互补的角，是∠AOE.

点评：在识图时，我们不仅要认真观察图形，而且还要仔细分析题设条件，这样才能作出正确的判断.