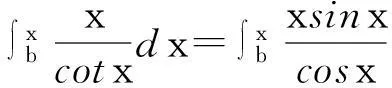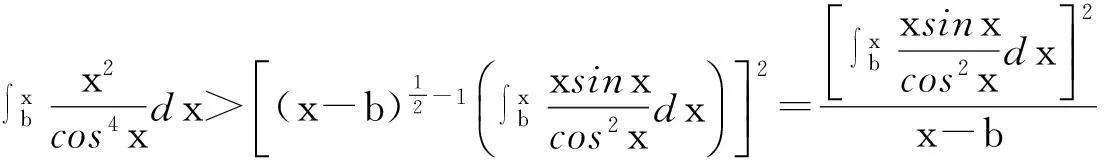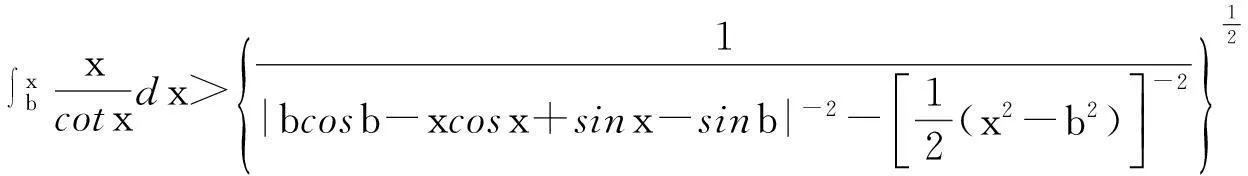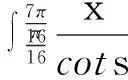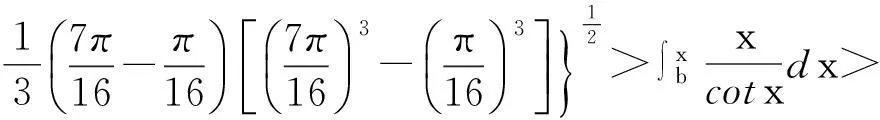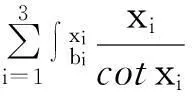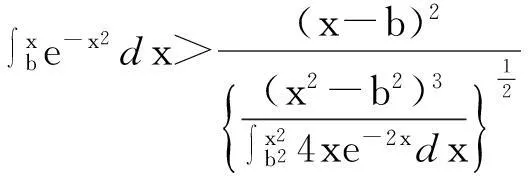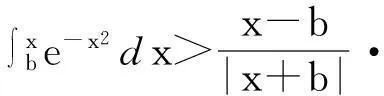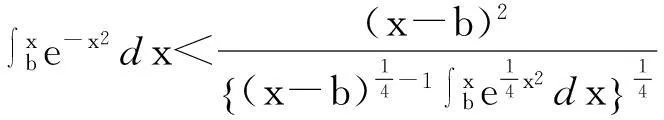定积分换元与积分不等式应用研究
王海舟
(硅湖职业技术学院, 江苏 昆山 215332)
定积分换元与积分不等式应用研究
王海舟
(硅湖职业技术学院, 江苏 昆山215332)
摘要:针对工程设计中的定积分换元和积分不定式的具体应用相关问题进行研究。通过具体运算,整理出一套函数积分近似计算公式,为计算机编程提供了重要的数学模型。
关键词:定积分; 积分不等式; 工程设计
0引言
对于现代的工程设计领域,定积分的积分不定式的出现,使得其工程设计的精度得到了很大提高。对于以前的那种定积分在计算上的大部分的计算难度和一些过程中的复杂程度。我们做了相应的改进和提高,减轻了其在计算上的一定难度,利用数学模型使其中一类定积分的计算过程变得不再那么复杂,简单明了。相对以前的那种在精度上、计算要求上都不是很高的一些计算方法,可以利用计算器进行手工的计算,还可以在不同情况下,把它们分成相等的部分,来计算出误差是多少。而对于精度要求比较高的过程设计计算来说,首先要做的就是把要进行使用的数学模型来编程,把其中积分区间的各个部分分得细一点。然后,再通过计算机对其中的数值来进行相应的计算。这种方法主要是针对在计算机中因为被积函数的原函数,不能使用其初等函数来表示积分中的近似计算可转化为实质的精确计算。
1定积分换元法的方法
定积分的换元法有很多种,其中在高等数学教材中主要运用以下定理:
定理1设f(x)连续,x=φ(t)有连续的导数,且φ′(t)≠0,则∫f(x)dx在[a,b]上存在,且

G(φ-1(x))+C
定理2若函数f(x)在[a,b]上连续,那么函数x=φ(t)满足下列条件:其一是φ(α)=a,φ(β)=b;其二是φ′(t)在[α,β](或[β,α])上有着连续的导数,而且a≤φ(t)≤b(α≤t≤β)。于是,就有了

这其中定理1证明了只需要等式两端去对x求导就行了。定理2也证明了一个简单的问题,那就是从条件中可以看出,在等号两边的被积函数都是连续的,再通过微积分的基本公式来进行相应的证明。
1.1 定积分换元方法1
根据定理1,可以知道其中有一条关键的就是φ′(t)≠0,为什么说它是比较关键的,因为在满足这个条件的时候,其保证了x=φ(t)的单调性。而这时函数x=φ(t)有着反函数,这样,才能使不定积分的换元法有效的实施开展。所以,在不定积分换元法的最后要求,对于代换函数x=φ(t)需要有其自身的反函数t=φ-1(x),不过,如果要对定理的条件进行专门研究,也可以用其它条件来代替,如果φ′(t)≠0,只要能够保证函数x=φ(t)有自身的反函数就可以。
1.2 定积分换元方法2
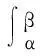
1.3 微分函数dx=φ′(t)dt
在求不定积分时,可以将其看成是一个一般的微分函数去计算,因为其结果都是函数。实质上没有什么特别的意义,不过,去求定积分时,因为它的结果是数值,所以dx=φ′(t)dt函数在实质上就有了一定的意义。其表示的是t轴上对于t处的一个增量dt,然后,在经过相应的变换后,函数x也就有了一个增量dx,其在数值上等于φ′(t)dt。这就是把dt在x=φ(t)上放大后的倍数变成了|φ′(t)|的形式。
2定积分换元法的研究
先设f(x)在[a,b]上是连续的,以此来证明

那么就需要去证明,先令t=a+b-x,这样x=a+b-t,这时dx=-dt,当x=a时,t=b,x=b时t=a。于是可以得到



最后得到[1]

可以利用这样的一个公式,得到以下结论;设f(x)在[a,b]上是连续的,如果λ+μ≠0,那么令
λf(x)+μf(a+b-x)=g(x)
则可以得到

因为
λf(x)+μf(a+b-x)=g(x)
所以可以证明

由

得出

又因为其公式λ+μ≠0,所以
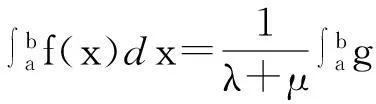
在这里比较特别的一点就是,如果要令f(x)+f(a+b-x)=g(x)的话,那么
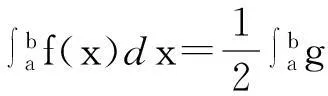
这个定理的主要意义就是当f(x)的定积分不太容易求出时,就可以通过它的组合式g(x)的定积分来相应的解决。
3定积分换元的应用结果


因为

所以

类似于这样的题目[3],我们一般都考虑使用连续的分部积分法来进行计算,让积分在等式两边出现,然后,通过方程再将其解答出来,这样的计算量是很大的,而你要使用本例子中的方法,那么将会简单的多。可以说是一种全新的突破,能够做到真正的事半功倍。
4积分不等式的主要研究

0 这时,对于 这个积分不等式是不成立的。 0 就会成立,主要因为其中 所以由上可得 现在由 得出 所以得出函数积分不等式 u=xsinx du=(sinx+xcosx)dx 然后就得出 并使之成立。再去证明第一个积分不等式的右边,得出了相应的积分不等式 由于一些同类的不等式的不等程度和异类的不等程度相比小得多,那么现在就以 所以,最后得出两个不定式 再求这个不等式的定积分,得出 综上所述,将上面的积分不等式再进行整理,从而最终得出积分不等式 并使其成立。 5积分不等式的主要计算实例 即 其计算上的误差 2.084 20-1.304 689=1.037 31 在积分区间未等分的情况下,积分的误差是最大的[4]。所以,现在将其进行3等分,使 那么对应的 这样再代入到上式中,可以得出 即得到 当积分被等分成3份的时候,积分的误差变小了很多,其误差是 1.753 371 193-1.534 336 015=0.219 035 178 如果想要得到更加精确的数值,那么就需要进行更加细致的等分[5]。 6定积分换元和积分不等式在工程设计中的应用 这个不等式能够成立,得出第二步 再由第二步和第三步得出 然后同理得出第四步 将第四步和第三步代入到第二步中,并将u记作x,得出第五步 将其整理得到 是成立的。那么,同样情况下,我们可以由第一步得出第六步 由第三、第四步得出第七步 这样,就可以同理,由第一步得出第八步 函数,由第五步得出第九步函数 我们运用前面的方法,将第九、第八和第七步一起代入到第六步中,在这里要将u记作x来算。得出了第十步函数式 使得我们知道 这个函数式是成立的。由上面的种种解析,我们知道,当积分区间分布的越细密,那么,这个不等式的不相等的可能性越小,等积分的上限x无限接近与积分的下线b时,那么,在这过程中的不同程度上,会趋向于零[7]。在f(x)=e-x2为偶函数时,那么,对于和原点区间对称的定积分,则可以利用其偶函数的性质进行相应的简化计算。 7主要探究实例 在积分中的区间未分开去算的话,积分的误差是最大的[5]。我们应该将积分分成4个相同的区间。现在是没有分开的积分u=x2,当x=0.6时,u=0.36,当x=0.7时,u=0.49,当x=0.8时,u=0.64,当x=0.9时,u=0.81,当x=1时,u也等于1。这样分别代入到积分不等式中,得出的计算结果是 0.048 471 539+0.040 497 119= 0.211 293 009 0.048 635 627+0.040 574 018= 0.212 345 798 0.212 345 798-0.211 293 900 9=0.001 052 798 可以看出,其误差比计算误差还要小。这就是对于积分区间在细分区间上的好处,如果想要更加的精确,那么就需要把积分区间分的更加详细。这样就会达到越详细、越精确的效果。 8结语 在当前工程技术发展中,我们在利用科学技术进行相应计算的同时,也在不断寻求更好的方法,使得在工程设计计算中的各项工作能够做到精确度的不断提升。在运用定积分换元和积分不等式,对工程设计进行计算时,往往会出现一些计算上或者是技术上的差错,这些都需要我们去进行不断的论证和探究,在进行计算时,采用计算机进行计算,然后,利用积分不等式以及定积分换元法细分区间的方法[7],能够方便在工程设计中出现,许多的因为被积函数不是初等函数的积分近似计算转化为实质上的运算。利用这样的方法,经过相关的研究和运算,整理出了一套函数的积分近似的计算公式,在为计算机编程的工作中,也作出了相当大的贡献,为其在编程上提供了两个重要的数学模型。这两个模型使计算机在编程上更加方便,也大大提升了其工程设计的计算精度。 参考文献: [1]李平乐,罗正斌,龙育才.工程设计计算新的数学模型的探索[J].焦作大学学报,2013(1):70-72. [2]李平乐,李春晖.另一积分不等式在工程设计中的应用[J].焦作大学学报,2014(1):80-83. [3]于正文.定积分线性换元法的教学研究[J].山东建筑大学学报,2012(2):255-258. [4]李平乐.基于工程设计计算新的积分不等式的研究[J].沈阳工程学院学报:自然科学版,2011(4):382-384. [5]张锐,毛耀忠,谢建民.浅议定积分的换元法[J].数学教学研究,2014(4):62-64. [6]韩仲明.定积分的计算方法与技巧[J].考试周刊, 2011,53:80-81. [7]高大维,冯世强,崔宇.不定积分与定积分第二类换元法的讨论[J].高等函授学报:自然科学版,2011(4):20-22. [8]杨镛.不定积分换元法的教学案例[J].教育教学论坛,2013(18):244-245. Application of definite integral element and integral inequality WANG Hai-zhou (Silicon Lake College, Kunshan 215332, China) Abstract:Based on the examples of definite integral element and integral inequality applied in engineering, we put forward an approximate figure of function integral, to offer a set of mathematical model for programming. Key words:definite integral; integral infinitive; engineering design. 作者简介:王海舟(1982-),男,汉族,江苏海安人,硅湖职业技术学院讲师,主要从事高等数学教学与应用方向研究,E-mail:40317414@qq.com. 收稿日期:2014-09-23 中图分类号:O 172.2 文献标志码:A 文章编号:1674-1374(2015)01-0114-07 DOI:10.15923/j.cnki.cn22-1382/t.2015.1.24