功率谱密度指导超光滑镜面加工
杨 晋, 尹 禄, 姚雪峰
(1.中国科学院长春光学精密机械与物理研究所, 吉林 长春 130033;
2.中国科学院大学, 北京 100049)
功率谱密度指导超光滑镜面加工
杨晋1,2,尹禄1,2,姚雪峰1
(1.中国科学院长春光学精密机械与物理研究所, 吉林 长春130033;
2.中国科学院大学, 北京100049)
摘要:根据双向反射分布函数反演功率谱密度,利用得到的功率谱密度函数指导镜面加工,理论推导结果合理,已经用于实际镜面加工。
关键词:功率谱密度; 双向反射分布函数; 镜面加工
0引言
光学反射镜在很多领域都起着至关重要的作用,其表面的光滑程度则决定了反射光的质量[1-2]。在很多光学精密仪器中,光学反射镜的光滑度决定着整个仪器杂散光的水平[3]。在设计对杂散光水平要求较高的仪器设备时往往需要对每一个反射镜的杂光水平提出指标要求。目前,一般使用双向反射分布函数(BRDF)来描述一个镜面的杂散光水平,但是国内反射镜研磨机构并没有直接针对BRDF参数进行反射镜加工的情况,这给反射镜设计者与加工者的参数对接提出了难题。鉴于此,文中对双向反射分布函数与反射镜面形评价作了研究,提出了根据BRDF指标反演功率谱密度(PSD)再利用功率谱密度函数指导镜面加工的方法。参考国外先进水平的BRDF指标进行实验仿真建模,计算其功率谱密度函数,计算结果可指导超光滑镜面加工。
1基本理论
1.1 光学元件的面形误差与功率谱密度[4]
反射镜等光学元件的面形误差可以根据其对入射光线不同的作用效果分为3个频段。周期小于0.12 mm是高频段,该频段属于表面粗糙度。由于高频段描述光学元件表面细微的起伏,微观状态下会对入射光线产生不确定方向的反射,在宏观中反映为散射效应。一般用均方根值RMS来评价:

(1)
式中:N----采样点个数;
x,y----表面位置横、纵坐标;
Z(x,y)----表面轮廓高度分布。
周期介于0.12~33 mm之间的是中频段,该频段属于表面波纹度。中频段的误差对成像的影响是一种衍射效应,难以用一般光线追迹的方法计算其对成像质量的影响,一般采用功率谱密度来评价:

(2)
式中:N----采样点个数;
D----采样间隔;
fm----第m阶空间频率;
Z----表面起伏高度。
周期大于33mm的是低频段,该频段属于表面面形。低频段表面面形误差主要影响入射光线主要能量的走向,与成像质量相关,一般采用PV值来评价:

(3)
式中:x,y----表面位置横、纵坐标;
Z(x,y)----表面轮廓高度分布。
根据式(2)可以看出,功率谱密度本质是表面面形函数各频率分量傅里叶振幅的平方和,它可以确定各个频率的分布情况,从而定量地计算出每一个频率分量对成像质量影响的贡献。
由于功率谱密度与光学元件的尺寸、使用位置无关,而且包含丰富的频谱信息,常用来评价光学元件的中频误差,但是它对整个频段的分析都有着重要的意义。
1.2 双向反射分布函数
双向反射分布函数(BRDF)是用来描述任意表面反射、散射等光学特性的数学模型。它是给定波长λ以确定的入射角入射到某一表面上的辐照度E与某一出射角度下的辐亮度L的比值:

(4)
式中:θ,θi----分别为散射光和入射光与法线的夹角;
φ,φi----分别为散射光和入射光与主平面的夹角;
Ps,Pi----分别为散射光和入射光光功率;
Ωs----散射光线立体角。
双向反射分布函数模型如图1所示。

图1 双向反射分布函数模型
根据BRDF的定义可以看出,它能够很方便地描述任意出射角下的光线强度,即杂散光强度。一般常采用改进的哈维模型来描述光学元件表面的散射特性,在该模型中相应的BRDF表达式可以写成:

(5)
式中:θs,θi----分别为散射光和反射射光与法线的夹角;
b0----散射角等于反射角时的BRDF值,是一个常量;
s----斜率;
l----肩宽。
哈维模型双向反射分布函数如图2所示。
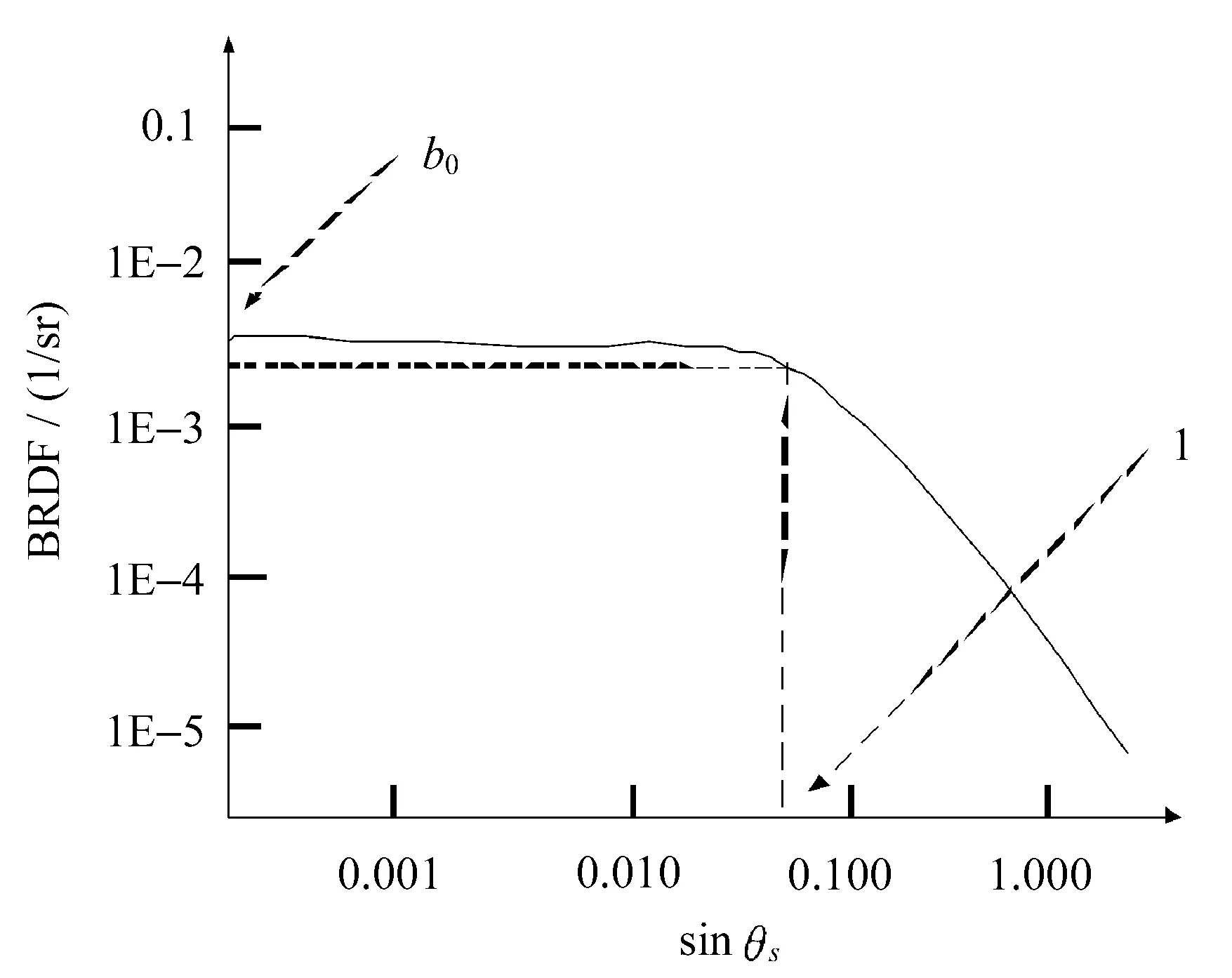
图2 哈维模型双向反射分布函数
2双向反射分布函数反演其镜面功率谱密度
由于低杂散光测试仪对仪器杂光具有非常高的要求,对于影响仪器杂光的关键器件反射镜来说,仅仅提出高频粗糙度的要求是远远不够的,必须配合中频波纹度的指标要求。目前,一般采用功率谱密度评价中频误差,国内尚无直接针对双向反射函数提出技术指标的情况。文中提出了将所需达到的BRDF指标换算成PSD的方法,利用PSD指导镜面加工以达到所需BRDF的指标。
BRDF与二维PSD的关系为[5-7]:

(6)
式中:f----空间频率;
Q----与入射角、散射角以及光线偏振方向有关的光学因子。
二维空间频率可以写为:

(7)

(8)
当只考虑一维方向时,方位角φ等于零,空间频率与入射角、散射角的关系可以写成:
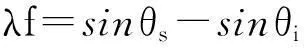
(9)
至此PSD与BRDF都可以转化为一维条件下入射角和散射角正弦的函数,其表达式为:

(10)
在不同偏振条件下,光学因子Q的表达式为[8]:

(11)

(12)

(13)

(14)
式中:θs,θi----分别为散射光和入射光与法线的夹角;
φ----散射光与主平面的夹角;
ε----镜面镀膜材料的复折射率。

(15)
式中:n----折射率;
k----消光率。
3实验建模
由文献[9]可知,美国国家航天局所使用镜面的粗糙度为2nm,参考波长为633nm时,b0=1.616 1,s=-1.852 6,l=5.062 5E-3,引用该组参数仿真镜面BRDF。对于复折射率N中参数,取折射率n=1.2,消光率k=7;入射角选择4.7°和45°。将上述参数代入式(10),可以解出一维PSD,如图3所示。
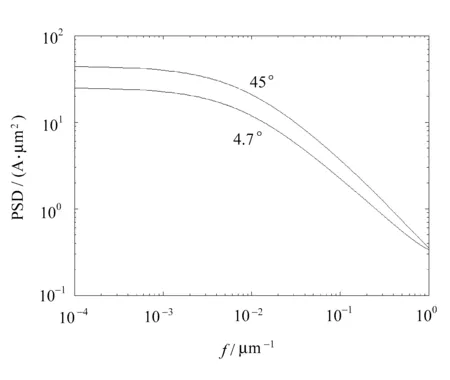
图3 一维功率谱密度
根据文中方法引用美国航天局镜面BRDF参数推导出的PSD已经用于指导镜面加工。
4结语
超光滑镜面在精密光学仪器中发挥着关键的作用,文中所提出的双向反射分布函数反演功率谱密度的方法可以建立超光滑镜面杂散光指标与镜面加工指标的直接联系,对指导超光滑镜面加工具有非常重要的意义。
参考文献:
[1]杜韦陶,宋丽,王玉柱,等.掠入射X射线散射法研究超光滑镜面粗糙度[J].核技术,2012,35(4):255-259.
[2]张军.一种空间遥感器反射镜柔性支撑结构[J].长春工业大学学报:自然科学版,2014,35(1):30-35.
[3]杨旺,黄玮,许伟才,等.光学表面中频误差对光刻物镜短程杂散光影响分析[J].光学学报,2013,33(9):0922001-1- 0922001-5.
[4]于瀛洁,李国培.关于光学元件波面测量中的功率谱密度[J].计量学报,2003,24(2):103-107.
[5]Egon Marx, Thomas A Germer, Theodore V Vorburger, et al. Angular distribution of light scattered from a sinusoidal gratin[J]. Applied Oaptics,2000,39(25):4473-4484.
[6]Michael G, Dittman. K-correlation power spectral density & surface scatter model[J]. SPIE,2006,6291:62910R-1-62910R-12.
[7]James E Harvey, Andrey Krywonos. Unified scatter model for rough surfaces at large incident and scatter angles[J]. SPIE,2007,6672:66720C-1-66720C-8.
[8]Thomas Weigel. Stray light test methods for space optical components[J]. SPIE,2010,30:691-699.
[9]Sholl M J, Grochocki F S, Fleming J C, et al. Stray light design and analysis of the SNAP telescope[J]. SPIE,2007,6675:66750C-1-66750C-12.
PSD guided ultra-smooth mirror finishing
YANG Jin1,2,YIN Lu1,2,YAO Xue-feng1
(1.Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China;
2.University of Chinese Academy of Sciences, Beijing 100049, China)
Abstract:Power spectral density, being deduced according to bidirectional reflectance distribution function, is used for guiding mirror finishing. The method is proved with theoretical derivation and has been applied to mirror finishing.
Key words:power spectral density; bidirectional reflectance distribution function; mirror finishing.
作者简介:杨晋(1988-),男,汉族,中国科学院长春光学精密机械与物理研究所研究实习员,博士,主要从事分光系统的光学设计研究,E-mail:yangjinl@mail.ustc.edu.cn.
基金项目:国家重大科学仪器设备开发专项项目(11YQ120023)
收稿日期:2014-06-13
中图分类号:O 411.3
文献标志码:A
文章编号:1674-1374(2015)01-0044-04
DOI:10.15923/j.cnki.cn22-1382/t.2015.1.09

