小波函数预测控制技术应用

赵泽福

(昭通学院 数学与统计学院， 云南 昭通　657000)



小波函数预测控制技术应用

赵泽福

(昭通学院 数学与统计学院， 云南 昭通657000)

摘要：利用小波的紧支局部特性以及多尺度分析方法，在时域范围内设置基函数的个数及位置分布以保证整体性能及拟合的逼近。仿真验证了该方法的可行性。

关键词：预测； 小波； 基函数

0引言

预测函数控制(PFC)是由Richalet与Kuntze提出的第三代模型预测控制算法，其快速的适应性、高精度算法控制以及较少的计算量使其已经广泛应用于机器人控制、雷达跟踪、热焓控制等领域[1]。近年来，PFC在工业领域得到了快速发展，其理论基础也得到不断完善，如PFC算法内模结构、一阶加纯滞后过程和二阶模型预测函数控制、自适应预测函数控制等。

针对不同的受控对象特性及其参考轨迹，在选择基函数时可取阶跃、斜坡、指数,甚至三角函数等[2]。该类基函数计算简单、意义明确，但目标函数均是全局函数，简化了优化要求或者仅对一两点进行拟合，不能发挥其整体预测优化能力，弱化了整体参考轨迹的预测逼近性能，降低了其抗干扰性和精确性。虽然基于傅里叶逼近思想的正弦多项式函数在控制性和适用性上得到了加强，但由于控制策略为滚动优化式，对于精确求解对象的当量控制及未来控制是不必要的。通常情况，参考轨迹的逼近可以通过预测函数的时域减弱特性，利用集结方式将优化变量用低维方式代替，这样不仅能够减少计算量，还可以提高计算速度，从而满足实时要求。针对时域减弱特性的灵活便捷设置，三角正弦函数同样也无法满足要求。文中提出的基于小波函数的预测函数控制技术方法通过实际仿真得到了有效验证。

1小波函数理论基础

小波理论是上世纪80年代应用数学和工程领域的重要产物。预测函数控制的基函数选择对于快速高精度控制极其重要，而小波的紧支局部特性以及多尺度分析特性弥补了全局函数的不足。与传统方法相比，小波通过伸缩和平移使得在时域和频域上具有很强的局部特性，根据需要可以将所研究的内容聚焦到任意微小的细节。对于PFC，当轨迹逼近要求较高精度时，可以选择小尺度的小波基函数，当对轨迹逼近精度要求低时，可以采用大尺度小波基函数。这样既可满足整体优化的同时，又兼顾了参考轨迹逼近的精度，在减少基函数的同时，也减少了权系数优化数量，完成了优化变量集结。基于此，文中将小波函数作为基函数应用于预测函数控制,利用加权最小二乘法计算权系数[3]。

设φ(t)∈L2(R)，当定义φ(t)为小波函数，则小波基函数为:

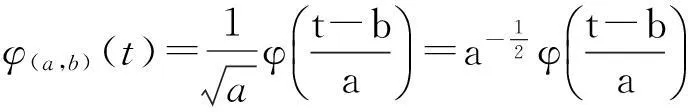
(1)

式中：a----尺度因子;

b----平移因子。

若a,b不断变化，则可得到新函数φa,b(t)。

根据小波函数定义可知,当函数φa,b(t)中的a发生变化时，可以反映出小波函数的不同尺度。随着a的不断增大，函数时宽增加，亦即用伸展的φ(t)去观察信号或函数f(t); 随着a的不断减小，函数时宽压缩，表示用压缩的φ(t)去观察信号或函数f(t)，亦即用尺度因子的变化来表征信号或函数f(t)的局部信息。通过小尺度的变化反映高频成分，大尺度的变化反映低频成分，以上特性便是小波的多尺度分析特性。另外，由于小波∫Rφ(t)dt<∞,φ(t)具有很快的衰减性，即是说φ(t)的非零域具有有限性，在时域范围内具有紧支集，很显然小波函数的局部化能力非常强，因此也就具备了时域紧支局部性。文中利用小波的紧支局部特性以及多尺度分析，通过对基函数的个数及位置分布在时域范围内的灵活设置，保证整体性能及拟合的逼近，实现了基于小波基函数的预测函数控制。

2基于小波函数的预测函数控制技术应用分析

预测函数控制的基础为模型预测控制，其模型基本特征主要包括3个方面：预测模型、滚动优化和反馈校正[4]。同时PFC自身也有相应的特点，主要为关键性的控制输入结构，通过预先选定的控制输入量作为基函数的线性加权，使输出作为对象的响应，实现目标函数的优化，求取加权系数，从而达到计算控制输入的目的。

2.1　预测模型

预测模型是预测函数控制的重要部分，主要用于描述目标对象的行为动态，预测过程的输出。对于其结构形式无需做过多的要求，重点在于完善其预测功能。预测系统的预测模型状态方程可表示为[5]:

Xm(k)=EmXm(k-1)+Fmu(k-1)

(2)

式中：Xm----状态向量,Xm∈Rn×1；

u----控制输入,u∈R1×1；

ym----预测模型输出,ym∈R1×1;

Em,Fm----状态方程系数矩阵,Em∈Rn×n,Fm∈Rn×1;

Cm----状态方程向量,Cm∈R1×n。

预测函数控制的具体形式为：

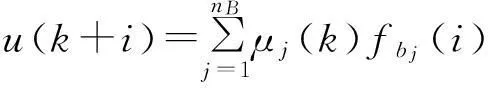
(3)

0≤i≤h

式中：μj----加权系数；

fbj----t=iT时的取值；

nB----基函数的个数；

h----时域长度。

预测模型的作用就是直接实现输入量对输出量的预测，模型的输出ym(k+i)可以表示为：

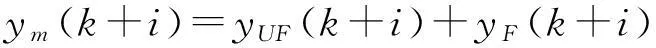
(4)

式中:yUF----自由响应输出，u=0；

yF----受迫响应。

其中yF可以由下式求得：

(5)

式中:fbj----在基函数fbj(i)作用下的模型输出。

由式(3)，(4)和式(5)得

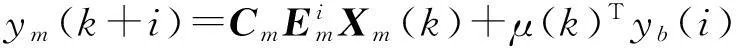
(6)

其中

μ(k)=[μ1(k),μ2(k),…,μnB(k)]T

yb(i)=[yb1(k),yb2(k),…,ybnB(k)]T

式(6)为模型输出,其中ybj(i)为在基函数ybj(i)作用下的线性叠加，只有加权系数μj(k)需要在线求解。

2.2　优化算法

预测函数控制优化的目标就是要找到一组系数，使得在整个优化时域内的预测输出尽可能接近参考轨迹。对于二次型性能指标可以通过拟合点上预测过程的输出yp与参考轨迹yR差值的平方和最小来表示[6]，即

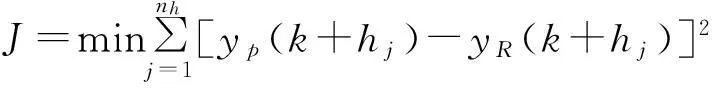
(7)

式中：nh----拟合点的个数，且nh≥nB;

hj----第j个拟合点的值。

参考轨迹选取指数形式：

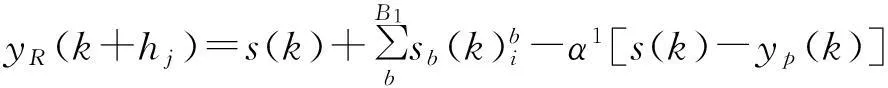
(8)

式中：yR(k+i)----(k+i)时刻参考轨迹的值；

s(k)----设定值轨迹；

yp----实际过程输出；

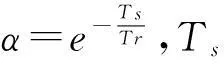
sb(k)----多项式系数；

Bs----多项式阶数[7]。

3仿真实例分析

文中以原油精馏塔为仿真对象，利用基于小波函数的预测函数控制方法进行仿真[8]，并将结果与传统算法进行对比。其输入输出对象模型可表示为：

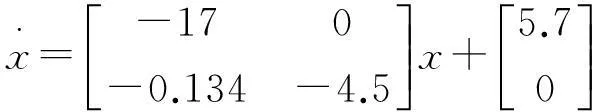
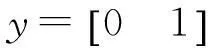
求出系统离散状态方程系数矩阵为:

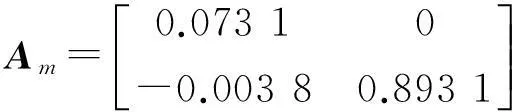
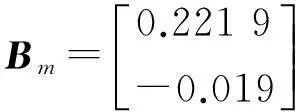
现假设模型Am,Bm失配而变为:

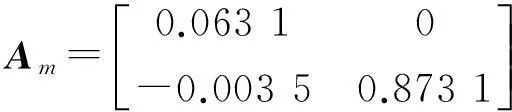
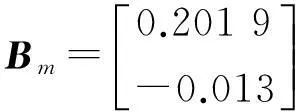
仿真参数选取：采样周期Ts=1 s；参考轨迹闭环响应时间Tr=1.5 s；预测时域优化长度H=8;仿真时间50 s。由此可得仿真效果如图1所示。

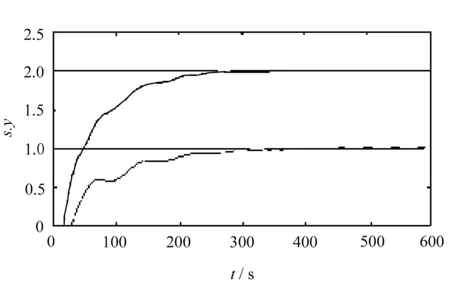
(a) 传统仿真效果

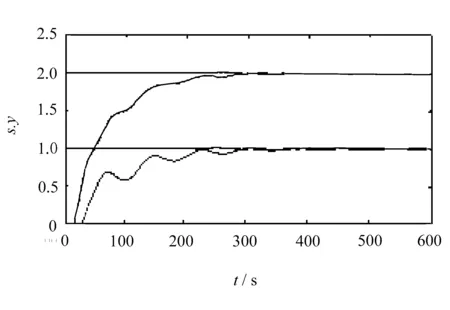
(b) 小波仿真效果图1　仿真对比图

由图1可以看出，文中提出的小波基函数的整体优化性能以及轨迹逼近精度均优于传统算法。

4结语

基于小波函数的预测函数控制方法有效地解决了传统预测函数中基函数的不足，利用小波函数的紧支局部特性以及多尺度分析特性完成了不同情况下的仿真比较。通过仿真结果可以得出，该方法计算简单、速度更快，对于工程应用更易实现。相比传统控制方法中的基函数在精度控制、参数变化抑制和抗干扰性能上有了较大程度的改善，在快速工程应用领域具有重要意义。

参考文献：

[1]Richalet J， RaultA， Testud J L， et al. Model predictive heuristic control: Applications to industrial processes[J]. Automatica,1978,14:413-428.

[2]侯宁,费树岷,周磊.基于小波函数的预测函数控制方法研究[J].西南大学学报：自然科学版,2014,36(2):136-142.

[3]郑军,颜文俊,诸静.基于小波基函数的预测函数控制[J].控制与决策,2005,20(9):1078-1080.

[4]杜晓宁,席裕庚.预测控制优化变量的集结策略[J].控制与决策,2002,17(5):563-566.

[5]AlbertB,FrancisJN.Afirstcourseinwaveletswithfourieranalysis[M].Beijing:PublishingHouseofElectronicsIndustry,2003:183-227.

[6]刘春雪,陈在平,董恩增.预测函数控制在网络控制系统的应用[J].天津理工大学学报,2009,25(1):29-32.

[7]潘红华,胡家升,朱森，等.一种改进的预测函数控制法[J].系统工程与电子技术,2003,25(11):1389-1391.

[8]周明月,姜文龙.基于小波变换的图像混合去噪算法[J].长春工业大学学报:自然科学版,2008,29(2):162-164.

A wavelet function based prediction method

ZHAO Ze-fu

(School of Mathematics and Statistics， Zhaotong University, Zhaotong 657000, China)

Abstract：With the local properties of wavelet and multi-scale analysis method, both the number and position of the basis functions, in time domain, are set to ensure the ensure the overall performance and fitting approach. Simulation has verified the feasibility of the method.

Key words：predictionl； wavelet function； basis function.

作者简介：赵泽福(1974-)，男，汉族，云南镇雄人，昭通学院讲师，主要从事基础数学及微积分方程竞赛数学方向研究,E-mail:mxc195611@163.com.

收稿日期：2015-01-25

中图分类号：O 174

文献标志码：A

文章编号：1674-1374(2015)01-0097-04

DOI:10.15923/j.cnki.cn22-1382/t.2015.1.20