水平互补问题二次优化求解
王秀玉, 李维娜
(长春工业大学 基础科学学院, 吉林 长春 130012)
水平互补问题二次优化求解
王秀玉,李维娜
(长春工业大学 基础科学学院, 吉林 长春130012)
摘要:水平互补问题转化为二次优化问题,通过求二次优化问题的K-K-T点获得水平互补问题的解。 给出了二次优化K-K-T点水平互补问题解的充要条件,以及水平互补问题有解和解集为凸集的充要条件。
关键词:水平互补; K-K-T方程; 行充分矩阵对; 列充分矩阵对
0引言
互补问题是数学最优化理论问题的重要分支,它不仅在数学的各个分支领域应用广泛,而且在实际生产中也被广泛应用。因此,对于互补问题的理论研究就显现得尤为重要。在过去几年中,很多人在这一领域进行了研究[1],给出了系数矩阵是半正定、或正定、或为P矩阵、或为P*等时线性互补问题解的存在问题[2],线性互补问题解的存在条件[3],线性互补问题的系数矩阵[4],正定矩阵的推广及其在线性互补问题中的应用[5]。文献[2]~[5]主要研究了下列形式的线性互补问题的系数矩阵:
找x∈Rn,使得y=Mx+q≥0,而且xTy=0。
其中, M∈Rn×n,q∈Rn。越来越多的专家不仅对理论层面进行了研究,而且在算法方面也有很多成果[6-8]。
线性互补问题是指在有限维实向量空间中寻找一个向量使之满足一定条件的不等式。特别地,如上述不等式所示。线性互补问题通常被称为二次优化的一个分支,大多数的专业数学研究者们认为线性互补问题和有限维最优化问题是等价的。线性互补问题的许多实例早于上世纪40年代就出现了,然而,对该问题的真正研究始于20世纪60年代。随着科技的不断向前发展,线性互补问题逐渐走入更多人的视野。文中主要研究下列形式的水平互补问题:
求x∈Rn,使得Mx+Ny+q=0,x≥0,y≥0,xTy=0。
首先,将水平互补问题转化为二次优化问题。第二,利用等价的二次优化问题,证明了二次优化的最优解(x*,y*)与乘子矢量u,v满足K-K-T条件。第三,二次优化问题的K-K-T点为水平互补问题的解的充要条件是系数矩阵对是行充分对。第四,解集S是凸集的充分和必要条件是系数矩阵对(M,N)是列充分矩阵对。总之,文中主要进行了线性互补问题解与系数矩阵对的研究。
在文中出现的所有向量,未强加说明的均为列向量。
1水平互补问题的相关定义
水平互补问题等价于下列最优值为零时的二次优化问题:

(1)
定义1矩阵M∈Rn×n被称为“列充分矩阵”,如对于任意的x∈Rn,有蕴含关系:
xi(Mx)i≤0 ⟹xi(Mx)i=0
i=1,2,…,n
定义2(M,N)称为行充分矩阵对,即对于∀z∈Rn,有下列蕴含式:
(MTz)∘(NTz)≥0⟹ (MTz)∘(NTz)=0
定义3(M,N)称为列充分矩阵对。若Mx+Ny=0,且x∘y≤0,则有x∘y=0。
定义4对矩阵A∈Rm×n,称其正生成锥为

文中记


v=v+-v-
|v|=v++v-
A=(M,N)
ri(pos(A))={u|u=Av,v>0}
α={i|xi>0}
α⊂I={1,2,…,n}

2水平互补问题的解集性质
定理1设
Mx+Ny=0
x≥0,y≥0
是可行的。则二次优化式(1)必有一对最优解(x*,y*),(x*,y*)与乘子矢量u,v满足K-K-T条件:

(2)
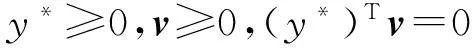
(3)

(4)
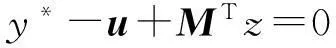
(5)

(6)
满足式(2)~式(6)的点称为水平互补问题的K-K-T点。且有K-K-T点为水平互补问题的解当且仅当(M,N)为行充分矩阵对。
证明根据K-K-T条件的充分性定理[2],可得水平互补问题(1)的K-K-T条件根据式(2)~(6)将式(5)和式(6)改写为如下形式:
MTz=u-y*
NTz=v-x*
所以,对于∀i=1,2,…,n
(MTz)i∘(NTz)i=(u-y*)i(v-x*)i=

(7)
(8)
且
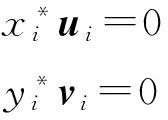
(9)
因此,由式(8)和式(9)可得,对于∀i=1,2,…,n有
(MTz)i∘(NTz)i=(u-y*)i(v-x*)i=
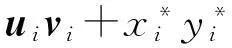
再由式(8)可得:
(MTz)i∘(NTz)i=(u-y*)i(v-x*)i=
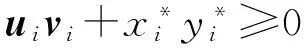
另外,因为已知(M,N)为行充分对,则由定义2必然可以推出对于∀z∈Rn,有
(MTz)∘(NTz)=0
成立。
所以
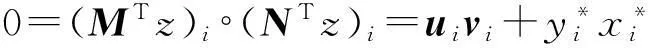
(10)
联立式(8)~式(10)必然有:

所以
x*Ty*=0
证明必要性:假设(M,N)不是行充分矩阵对,那么,必∃z∈Rn,z≠0,使得
(MTz)∘(NTz)≥0
并且,∃k,使得
(MTz)k∘(NTz)k≥0
等价于
(MTz)∘(-NTz)≤0
且,∃k,使得
(MTz)k∘(-NTz)k<0
不妨设(MTz)k<0,(-NTz)k>0。
取
x=(-NTz)+
y=(MTz)-
因此有
-NTz=(-NTz)+-(-NTz)-
MTz=(MTz)+-(MTz)-
令

那么

令
u=MTz+y=MTz+(MTz)-=
(MTz)+≥0
令
v=NTz+x=NTz+(-NTz)+=
(-NTz)+-(-NTz)=
(-NTz)-≥0
(x,y,u,v)满足优化问题的K-K-T方程,即为K-K-T点。另外
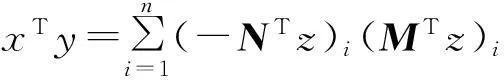
又
(MTz)-∘(-NTz)+≥0
故
xTy≥0
又,∃k,使得

因此
xTy≥0
这与
xTy=0
矛盾。
所以(M,N)是行充分对,即命题成立。证毕。
定理2令S={(x,y)|Mx+Ny+q=0,x≥0,y≥0,xTy=0},那么S为凸集 ⟺(M,N)为列充分矩阵对。






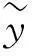

所以

那么


i=1,2,…,n
因(M,N)为列充分矩阵对,由定义3可得

又

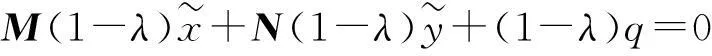
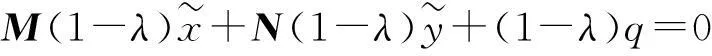
故

令


则
Mx(λ)+Ny(λ)+q=0
又因为,x(λ)≥0,y(λ)≥0,且
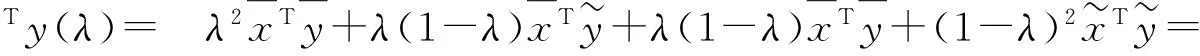
λ2×0+λ(1-λ)×0+λ(1-λ)×0+λ(1-λ)2×0=0
因此有(x(λ),y(λ))∈S。故S为凸集。
必要性:已知S为凸集,往证(M,N)为列充分对。
假设(M,N)不是列充分矩阵对,即∃(u,v)
Mu+Nv=0
u∘v≤0
且∃k
ukvk<0
取x=u+
u=u+-u-
Mu=Mu+-Mu-
y=v+
v=v+-v-
Nv=Nv+-Nv-
令

那么

即
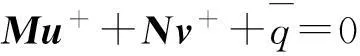
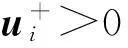
ui>0
vi≤0
则
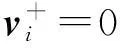
必有

同时

-Mu+-Nv+=
-(Mu+Mu-)-(Nv+Nv-)=
-Mu-Mu--Nv-Nv-=
-Mu--Nv-
所以


即
(u+,v+)∈S
(u-,v-)∈S
因S为凸集,故对∀λ∈[0,1],必有
(λu++(1-λ)u-,λv++(1-λ)v-)∈S
然而
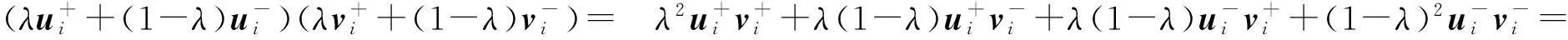
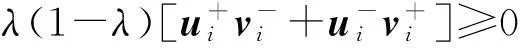

因此,(M,N)为列充分矩阵对。
定理3水平线性互补问题x≥0,y≥0,且xTy=0, Mx+Ny=-q有解⟺-q∈pos(Cα(A))
其中
A=(M,N)
证明必要性:已知x≥0,y≥0,且xTy=0时,Mx+Ny=-q有解,往证-q∈pos(Cα(A))。
因为Mx+Ny=-q有解,因而-q=Mx+Ny可以改写成

令
α={i|xi>0}
则

同时记
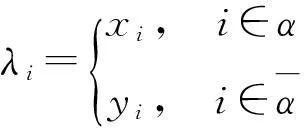
那么
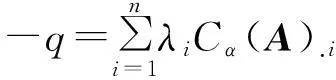
故
-q∈pos(Cα(A))
必要性得证。
证明充分性:已知-q∈pos(Cα(A)),往证x≥0,y≥0,且xTy=0时,Mx+Ny=-q有解。
因为-q∈pos(Cα(A)),因此存在一系列的xi,yi,使得

那么

因而
Mx+Ny=-q
有解。充分性得证。
定理4解集S为凸集⟺ri(pos(Cα(A))∩ri(pos(Cβ(A))=Ø,∀α≠β⊆I。
证明必要性。
已知解集S为凸集,往证
ri(pos(Cα(A))∩ri(pos(Cβ(A))=Ø
∀α≠β⊆I
可得

反证法:设∃α≠β⊆I,使得
ri(pos(Cα(A))∩ri(pos(Cβ(A))≠Ø
那么,必然可得
∃-q∈ri(pos(Cα(A))∩ri(pos(Cβ(A))
故


再者,由ri(pos(Cα(A))∩ri(pos(Cβ(A))≠Ø和定理3的充分性可推出,Mx+Ny=-q有解。
因此
(x(1),y(1))∈S
(x(2),y(2))∈S
由S为凸集可知,对于∀ 0≤λ≤1,有
(λx(1)+(1-λ)x(2),λy(1)+(1-λ)y(2))∈S
因而
[λx(1)+(1-λ)x(2)]T[λy(1)+(1-λ)y(2))]=λ(1-λ)[x(1)Ty(2)+x(2)Ty(1)]
又因为对于
∀α≠β⊆I
有

因此
λ(1-λ)[x(1)Ty(2)+x(2)Ty(1)]>0
矛盾。故
ri(pos(Cα(A))∩ri(pos(Cβ(A))≠Ø
∀α≠β⊆I
充分性:已知
ri(pos(Cα(A))∩ri(pos(Cβ(A))=Ø
∀α≠β⊆I
往证S为凸集。
假设S非凸,且∃-q使得

其中



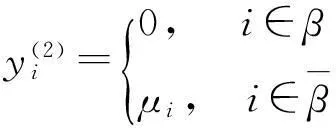
再者,对于
∀α≠β⊆I
有

必然可得∃k,使得
λk>0
μk>0
U.k=M.k
V.k=N.k
记
γ={i|U.i=V.i}
那么必有

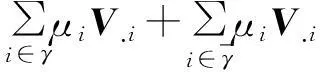
另外,记




令
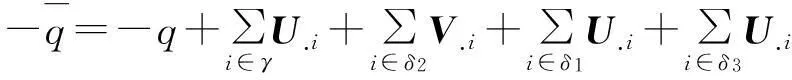


同时


这与
ri(pos(Cα(A))∩ri(pos(Cβ(A))=Ø
对于
∀α≠β⊆I
矛盾。
因此,充分性成立。证毕。
参考文献:
[1]袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,1997.
[2]韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:上海科学技术出版社,2006.
[3]雍龙泉,刘淳安.线性互补问题解得存在条件[J].宝鸡文理学院学报,2005(4):262-264.
[4]孙艳波,线性互补问题的相关矩阵研究[J].科学技术与工程,2008(10):2518-2522.
[5]雍龙泉,正定矩阵的推广及其在线性互补问题中的应用[J].广西科学,2007,14(2):120-121.
[6]姜兴武,王秀玉.P0线性互补问题的新同伦方法[J].吉林大学学报,2013(5):807-810.
[7]徐俊彦,苗壮,谭佳伟,等.解线性互补问题的组合同伦方法[J].长春工业大学学报:自然科学版,2010,31(3):269-274.
[8]徐俊彦,苗壮,刘庆怀.解广义水平线性互补问题的组合同伦方法[J].吉林大学学报,2010(3):647-653.
Quadratic optimization algorithm for
the horizontal complementarity problem
WANG Xiu-yu,LI Wei-na
(School of Basic Sciences, Changchun University of Technology, Changchun 130012, China)
Abstract:The horizontal complementarity problem is transformed into quadratic optimization to get the solution of horizontal complementarity by obtaining the K-K-T point quadratic optimization. We give the necessary and sufficient conditions for both the K-K-T point quadratic optimization and with solution and convex set solution horizontal complementarity problems.
Key words:horizontal complementarity; K-K-T equation; row sufficient; column sufficient.
作者简介:王秀玉(1965-),女,汉族,吉林长春人,长春工业大学教授,硕士,主要从事最优化理论与算法方向研究,E-mail:wangxiuyu@ccut.edu.cn
基金项目:国家自然科学基金资助项目(10771020); 吉林省自然科学基金资助项目(201215128,20101597)
收稿日期:2014-06-13
中图分类号:O 221.2
文献标志码:A
文章编号:1674-1374(2015)01-0101-06
DOI:10.15923/j.cnki.cn22-1382/t.2015.1.21

