慎用等效后的物理概念

王小玲

一次，两位学生相跟着来问我这样一个题：

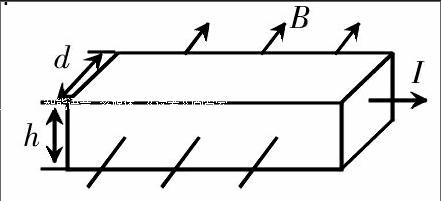
如图所示，厚度为h、宽度为d的金属导体，当磁场方向与电流方向（自由电子定向移动形成电流）垂直时在上下表面会产生电势差，这种现象称为霍尔效应。下列说法正确的是（ ）

A.上表面的电势高于下表面

B.下表面的电势高于上表面

我很好奇，难道是不清楚霍尔效应产生的原因？

学生：不是。霍尔效应中，上下两表面之所以存在电势差，是定向移动的自由电荷在洛伦兹力的作用下发生偏转，聚集在上（或下）表面上造成的。哪个表面的电势高，则取决于电荷的电性及聚集在哪一表面。

我就更加莫名其妙了，那问题是什么呢？

甲学生：老师，电流方向向右，可认为是正电荷在向右定向移动，由左手定则可判定，洛伦兹力的方向向上，所以上表面会聚集正电荷，使上表面电势升高，应选A。

乙学生紧跟着说：可实际上，金属中定向移动的是自由电子，电流方向向右，可判定自由电子是在向左做定向移动，同理可得出，自由电子是向上表面偏转，结果，上表面聚集负电荷，上表面的电势低，故应选B。

然后，两学生异口同声地说：我们认为两种推断均有道理，都应该是正确的，可两者结果却是相反的，这是怎么回事？是哪个错了？哪儿错了？为什么都向上表面偏呢？

我听完后，也有点发蒙。

仔细分析甲、乙两学生的的推断，他们依据的理论是相同的，区别之处在于运动的电荷，甲为正电荷向右运动，乙为负电荷向左运动，运动电荷的电性及运动方向都正好相反。而在磁感应强度B相同的情况下，洛伦兹力的方向取决于电荷的电性和运动方向这两个因素，且有否定之否定，即为肯定的特点，也就是说，一个因素相反，则洛伦兹力的方向相反；若两个因素相反，则洛伦兹力的方向相同。从而导致甲、乙的推导中，无论是正电荷还是负电荷均向上表面偏转的结果。这同时也说明问题出在运动电荷的确定上。

对于运动电荷的确定，乙是“可判定”，是真实情境；甲是“可认为”，是一种等效替代，可若替代的结果与实际不同（在此处竟为截然相反），说明不能进行等效替代。

学生还是很疑惑：可是，老师，不是说在电路中，尽管定向移动的是自由电子，但为了表述方便，常用正电荷向相反方向定向移动来进行等效替代吗？而且教材在推导电流的功、计算电解液中的电流时都用了这种等效替代，为什么在这儿就不能进行等效替代？

的确，教材中明确给出，规定正电荷定向移动的方向为电流的方向；又补充说，负电荷定向移动的反方向也为电流的方向。之所以这样说，是电荷定向移动的动力为电路中静电场所施加的静电力，在电路中，静电场的方向是确定的，故正、负电荷所受静电力的方向相反，定向移动的方向也相反；而根据相对运动，无论是哪种电荷定向移动，正电荷相对于负电荷都是在沿静电力方向移动，即以负电荷为参考系，静电力定向移动电荷的结果是相同的；再者，负电荷向静电力的反方向移动，使静电力方向净正电荷数目增多，从净电荷量上而言，与正电荷在沿静电力方向移动的效果相同；所以，在研究净电荷的数量（电流的大小）或者是静电力移动电荷（电流的方向）的物理情境时，用哪一种均可，即研究电流时，可以进行这种等效替代。

可为什么在霍尔效应中，也涉及电流，却不能进行这种等效替代呢？

等效替代是物理学中常用的一种思维方式，利用它，可以把复杂的问题简单化，把难以处理的问题具体化。但既然称之为等效替代，就说明这种替代与实际情境是不同的，只是在特定的条件下，或者说对于特定的研究问题和情境，才有替代前后的效果相同，故由此建立的一些概念和规律也是有适用条件的，或者说只适用于此特定的研究问题和情境。例如，质点这一等效概念，在研究地球公转时，地球可看作质点，但若研究的是地球自转，就不能看作质点了。这是因为质点是建立在物体的大小、形状对所研究的问题没有影响或者是影响比较小的前提条件下。又如，交流电的有效值，是从能量的角度利用等效替代去描述交变电流的特征的，故在交变电路中，研究保险丝是否会熔断，比较的是保险丝的实际功率与额定功率的大小，是能量，用有效值；而电容器是否会被击穿，比较的是电压，故不能用有效值，只能用瞬时值。

在电流的概念中，正电荷对负电荷的这种等效替代，是建立在静电力移动电荷这一物理情境上；电解液中的电流，与它的物理情境相同，可进行等效替代；电流的功是静电力对定向移动的电荷所做功的宏观效应，研究的情境实质也是静电力移动电荷，故

也可等效替代。而在霍尔效应中，所研究情境不再是静电力移动电荷，而是洛伦兹力移动电荷，情境已发生了变化，能否同样进行等效替代，必须得看替代后的结果是否一致，这儿明显不同。

学生恍然大悟。

等效替代是有前提条件的，等效替代后得到的概念或规律是有其适用情境的，要把它做迁移使用，必须得谨慎。

参考文献：

杨东冬.中学物理概念教学研究[D].陕西师范大学，2012.

编辑 温雪莲