巧用基本图形，提高解题效率

李密

在几何计算和证明的实践活动中，图形往往是千变万化的，从而使学生在解题过程中难以抓住图形的本质和重点，对题目所给信息不能正确提取和重组，找不到解决问题的突破口，这是造成学生觉得几何难学的主要原因，但是，任何一个复杂的几何图形都是由相关的基本图形所构建、整合而成的，也就是说一个几何问题往往是多个知识点的有机整合。因此，对复杂图形进行合理分解，然后根据基本图形可以为学生寻找解题的突破口提供线索，有效防止无关信息干扰，找到解题突破口，提高思维的敏

捷性。

一、基本图形

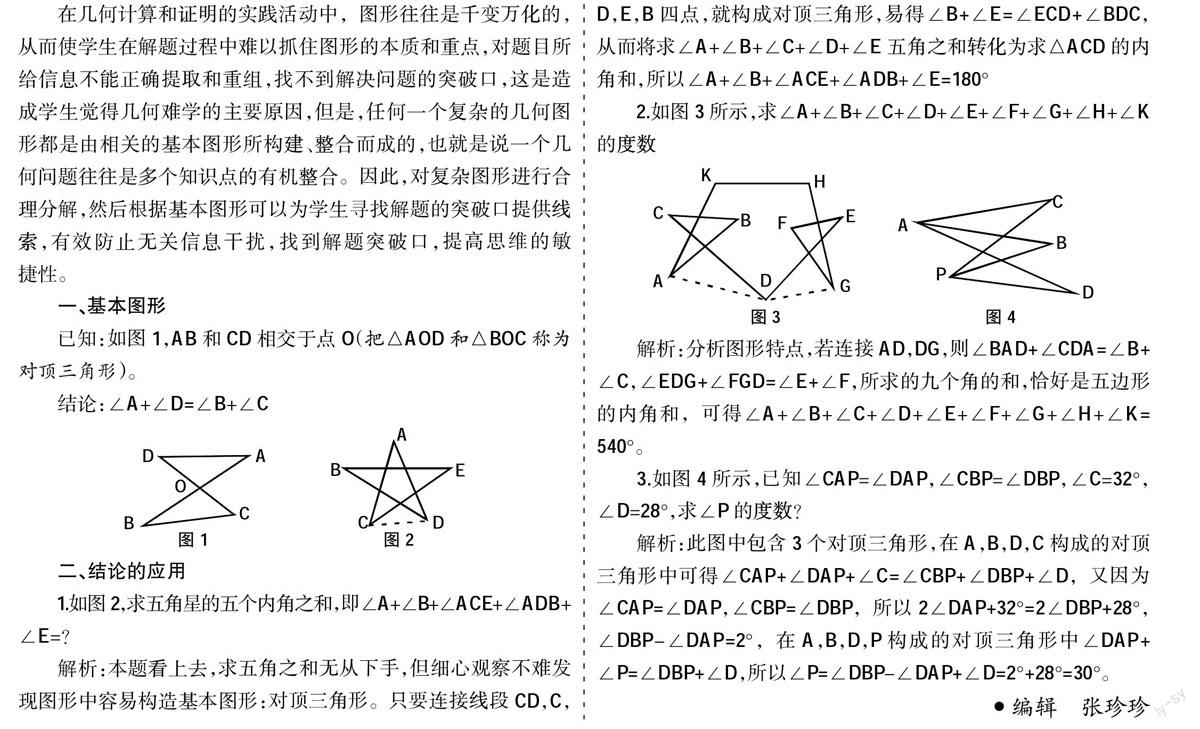
已知：如图1，AB和CD相交于点O（把△AOD和△BOC称为对顶三角形）。

结论：∠A+∠D=∠B+∠C

二、结论的应用

1.如图2，求五角星的五个内角之和，即∠A+∠B+∠ACE+∠ADB+∠E=？

解析：本题看上去，求五角之和无从下手，但细心观察不难发现图形中容易构造基本图形：对顶三角形。只要連接线段CD，C，D，E，B四点，就构成对顶三角形，易得∠B+∠E=∠ECD+∠BDC，从而将求∠A+∠B+∠C+∠D+∠E五角之和转化为求△ACD的内角和，所以∠A+∠B+∠ACE+∠ADB+∠E=180°

2.如图3所示，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K的度数

解析：分析图形特点，若连接AD，DG，则∠BAD+∠CDA=∠B+∠C，∠EDG+∠FGD=∠E+∠F，所求的九个角的和，恰好是五边形的内角和，可得∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K=540°。

3.如图4所示，已知∠CAP=∠DAP，∠CBP=∠DBP，∠C=32°，∠D=28°，求∠P的度数？

解析：此图中包含3个对顶三角形，在A，B，D，C构成的对顶三角形中可得∠CAP+∠DAP+∠C=∠CBP+∠DBP+∠D，又因为∠CAP=∠DAP，∠CBP=∠DBP，所以2∠DAP+32°=2∠DBP+28°，∠DBP-∠DAP=2°，在A，B，D，P构成的对顶三角形中∠DAP+∠P=∠DBP+∠D，所以∠P=∠DBP-∠DAP+∠D=2°+28°=30°。

编辑 张珍珍