拉格朗日中值定理在方程有根证明题中的应用

尹逊波，吴勃英，白　红

(哈尔滨工业大学数学系，哈尔滨150001)



拉格朗日中值定理在方程有根证明题中的应用

尹逊波，吴勃英，白红

(哈尔滨工业大学数学系，哈尔滨150001)

[摘要]对微分中值定理证明方程有根的题型作了分类，分析并讨论了证明中的技巧，及证明中所采用的方法，并对不同例子进行了相应的拓展.

[关键词]高等数学; 中值定理; 证明

高等数学是理工科院校一门十分重要的公共基础课，而其中证明题在培养和训练学生的创新能力方面起着重要的作用[1-2].中值定理所涉及的几个定理经常被用来证明等式及不等式.而其中的拉格朗日中值定理就是既可常用来证明不等式，又可用来证明方程有根，但拉格朗日中值定理在证明方程有根是和罗尔定理有所不同的. 下面先通过几个例子来看一下拉格朗日中值定理的应用.

例1设f(x)在[0，1]上连续，在(0，1)内可导，f(0)=f(1)，证明：存在两个不同点ξ，η∈(0，1)，使得f′(ξ)+f′(η)=0.

分析寻找(0，1)内的一个点c，利用两次拉格朗日中值定理，即可以得到两个不同的点ξ，η∈(0，1)

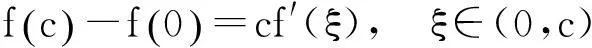
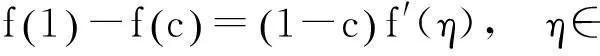
两式相加，得

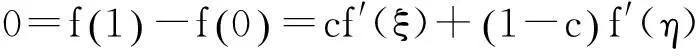
证由拉格朗日中值定理

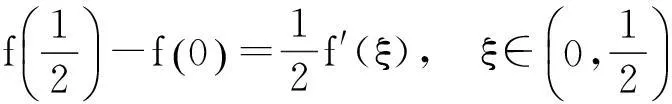
(1)

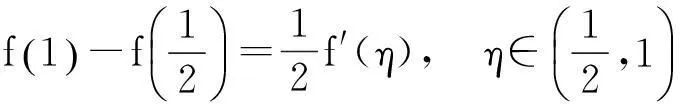
(2)

(1)+(2)，得

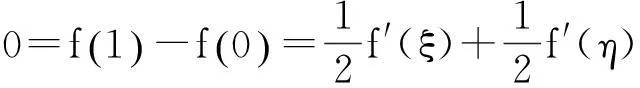
即

f′(ξ)+f′(η)=0.

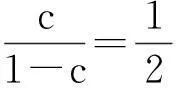
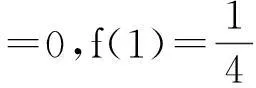
分析将要证明的结论“f′(ξ)+f′(η)=ξ3+η3”变形，得到

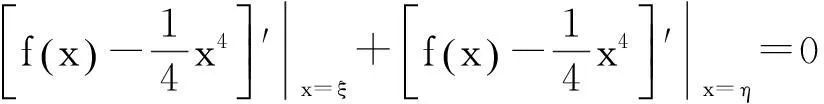
(3)

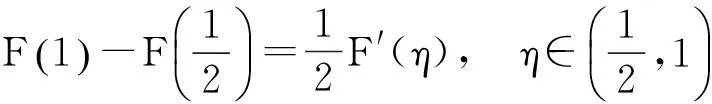
(4)

(3)+(4)，得

0=F′(ξ)+F′(η).

即

f′(ξ)+f′(η)=ξ3+η3.

注同例1一样，也可以将此题推广，但需要注意对应的ξ和η必须是同步的，即需要是相同类型的函数.

例3(2005年研究生入学考试数一(18)题)设f(x)在[0，1]上连续，在(0，1)内可导，f(0)=0，f(1)=1，证明：

(i) 存在ξ∈(0，1)，使得f(ξ)=1-ξ.

分析难点主要在第二问，但有了第一问的ξ，实际上由例1和例2可知，ξ即为内部的特殊点c.

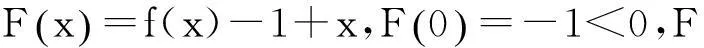
(ii) 由拉格朗日中值定理

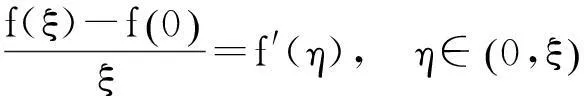
(5)

(6)

由(5)，(6)分别得

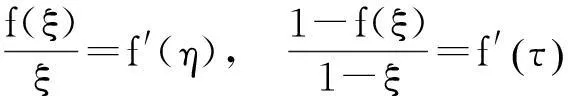
故

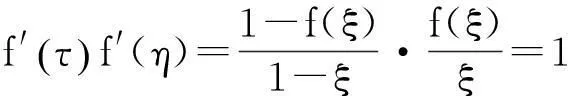
例4设f(x)在[0，1]上连续，在(0，1)内可导，f(0)=0，f(1)=1，证明：任给a，b>0，在(0，1)内一定存在互不相同的ξ，η， 使得

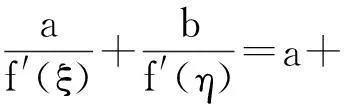
分析寻找(0，1)内的一个点c，利用两次拉格朗日中值定理

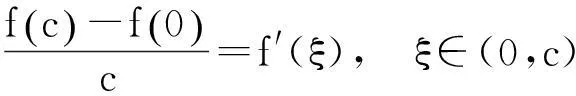
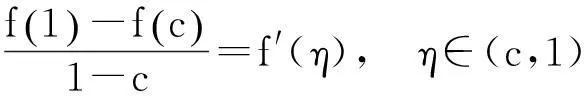
化简得

需满足

容易看到，当取

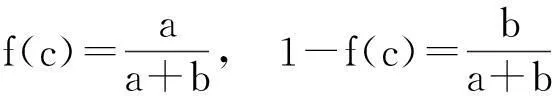
时，上式成立.

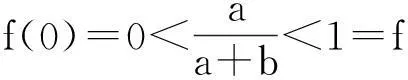
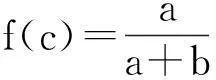
再由拉格朗日中值定理

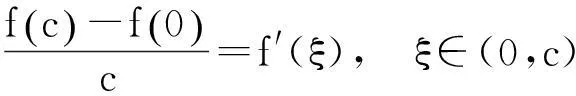
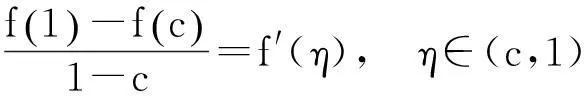
则

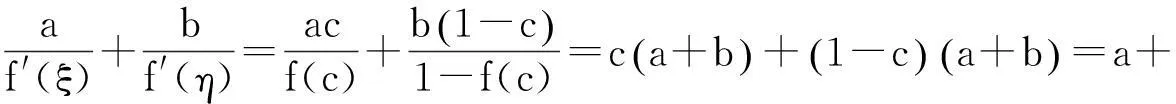
由前面的例子，不难发现，拉格朗日中值定理证明方程有根的题目与罗尔定理证明方程有根的题目是有很大不同的，它所证明的结论中一般对应的方程通常的二元方程，而罗尔定理所证明的方程有根的题目通常是一元方程. 不管哪种，只要掌握了它的规律都不难给出证明.

[参考文献]

[1]哈尔滨工业大学数学系分析教研室.工科数学分析(上册)[M].北京：高等教育出版社，2013.

[2]曾可依. 从几何的角度看微分中值定理[J].大学数学，2014，30(2): 108-111.

Applications of Larange Mean Value Theorem in the Proof of

Equations Which Have Roots

YINXun-bo，WUBo-ying，BAIHong

(Department of Mathematics, HIT, Harbin, Heilongjiang 150001, China)

Abstract:The types of equations which have roots proved by the differential mean value theorem are classified， and the techniques of the proofand the method used in the proof are analyzed and discussed. And the different examples are promoted in corresponding.

Key words:higher mathematics; the differential mean value theorem; proof

[基金项目]省教改项目“数学主干课的信息化建设 ”(JG2014010728)

[收稿日期]2015-01-06

[中图分类号]O13

[文献标识码]C

[文章编号]1672-1454(2015)02-0084-03