轻质模型在牛顿运动定律中的应用
金年庆

中学物理研究的问题都以模型为主,轻弹簧、轻绳、轻杆就是最常见的三类理想化模型,三类模型是高考命题的重点,本文重点讨论轻质模型在牛顿运动定律中的应用.
所谓“轻质”就是忽略模型的质量,即m=0,根据牛顿第二定律F合=ma,物体所受的合外力为O,这是解题的关键.
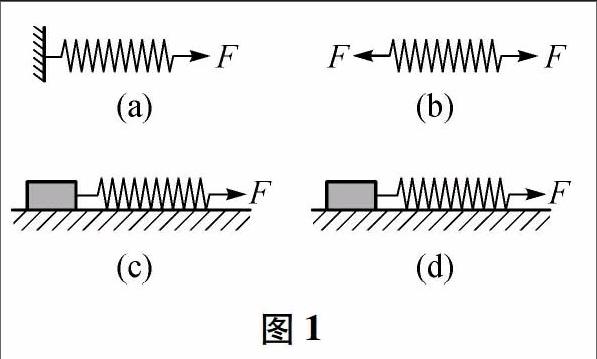
例1如图1所示,4个完全相同的弹簧都处于水平位置,它们的右端受到大小皆为F的拉力作用,而左端的情况各不相同:(a)弹簧的左端固定在墙上;(b)弹簧的左端受大小也为F的拉力作用;(c)弹簧的左端拴一小物块,物块在光滑的桌面上滑动;(d)弹簧的左端拴一小物块,物块在有摩擦的桌面上滑动.若认为弹簧的质量都为零,以ι1、ι2、ι3、ι4依次表示4个弹簧的伸长量,则有()
A.ι2>ι1
B.ι4>ι3
C.ι1>ι3
D.ι2=ι4
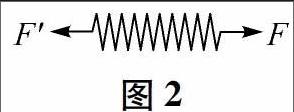
解析 设弹簧的质量为m,运动加速度为a,研究弹簧,其受力如图2所示.
由牛顿第二定律有F-F'= ma
因为弹簧的质量m=0,所以F=F'
题述中4种情况弹簧两端受力大小都为F.所以选项D正确.
点评本题最容易犯的错误就是凭经验,想当然的认为ι1=ι2>ι4>ι3.其实只要抓住本质就很容易解题:m=0,根据牛顿第二定律,F合=0.
例2 如图3所示,倾角为a的等腰三角形斜面固定在水平面上,一足够长的轻质绸带跨过斜面的顶端铺放在斜面的两侧,绸带与斜面间无摩擦.现将质量分别为M、m(M>m)的小物块同时轻放在斜面两侧的绸带上.两物块与绸带间的动摩擦因数相等,且最大静摩擦力与滑动摩擦力大小相等.在a角取不同值的情况下,下列说法正确的有
()
A.两物块所受摩擦力的大小总是相等
B.两物块不可能同时相对绸带静止
C.M不可能相对绸带发生滑动
D.m不可能相对斜面向上滑动
解析本题中有三个物体可视为研究对象:轻质绸带和两个小物块.
1.取轻质绸带为研究对象,沿斜面方向建立如图4所示的坐标系,只考虑轻质绸带沿斜面方向的受力.轻质绸带的质量m=0,根据牛顿第二定律F合=ma,它所受的合外力为O,则两物块对它的摩擦力f1和f2一定大小相等、方向相反(沿图示坐标轴方向),如图5所示.
2.分别取M和m为研究对象,受力分析如图6所示,根据牛顿第三定律,f'1,和f'2大小相等、方向相反(沿图示坐标轴方向).由于朋>m,N1>N2,两物块与绸带间的动摩擦因数相等,且最大静摩擦力与滑动摩擦力大小相等.显然,f'1和f'2不可能同时为滑动摩擦力,只有两种可能:
(1)f'1为静摩擦力f'2为滑动摩擦力:物块M与绸带相对静止,物块m与绸带相对滑动,即物块M和绸带一起沿x轴正方向加速运动,物块m也沿x轴正方向加速运动,但物块M和绸带的加速度大于物块m的加速度;
(2)f'1和f'2均为静摩擦力:物块M和物块m均与绸带相对静止,即物块M和物块m及绸带一起以共同的加速度沿x轴正方向运动(沿图示坐标轴方向).
综合以上分析,本题正确答案为AC.
点评 本题对学生来说难度比较大,很多同学只能凭感觉瞎猜,不能正确解答本题.其实,解答本题的前提就在于找准合适的研究对象,弄清分析的顺序.解题的关键在于抓住轻质绸带的质量为O,则合外力一定为O,所以它的受力应该是明确的.
例3某缓冲装置的理想模型如图7所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力为定值.轻杆向右移动不超过ι时,装置可安全工作.若一小车以速度vo撞击弹簧,已知装置可安全工作,轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面间的摩擦.从小车与弹簧刚接触时开始计时,下列关于小车运动的速度一时间图象可能正确的是
()
解析 杆的质量不计,所受合外力为零,故杆受到弹簧的力F和槽的摩擦力大小始终相等,这是解题的关键.
(1)若初速度vo较小,在弹簧被压缩过程中,由于杆的质量不计,所受合外力为零,故弹簧给杆的力F与槽给的静摩擦力大小相等,最初杆不动.小车与弹簧接触时开始做加速度增大的减速运动,当小车减速为0时,轻杆仍没运动,然后小车反向做加速度减小的加速运动,离开弹簧后的速度大小仍为vo.小车以vo与弹簧接触,轻杆开始移动时,弹簧的弹力F=f,而F=kx,解得x=f/k
(2)若初速度vo较大,当小车与弹簧接触时开始做加速度增大的减速运动,当弹簧弹力大于最大静摩擦力时,杆开始移动,由于杆受到的滑动摩擦力f不变,而“轻”杆这一条件约束着弹簧的力也始终限定在等于,故弹簧长度被锁定,车与杆作为整体,小车和弹簧一起做匀减速直线运动直到速度为0,然后小车反向做加速度减小的加速运动,由于有机械能损失,小车离开弹簧时的速度小于vo,所以选项A、D正确.
以牛顿运动定律运动定律为基础的动力学问题是高考考查的重点和难度,解题的关键在于正确的理解模型,抓住本质.对轻质模型而言,就在于抓住其“轻”的本质——质量为0,合外力为0.
——不计质量的力学模型
——2011年高考江苏卷第9题

