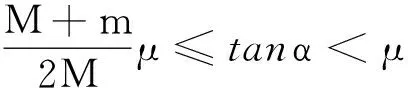对2011年高考江苏物理试卷第9题的再探讨
汪飞
(江苏省海门中学 江苏 南通 226100)
1 问题的提出
【题目】(2011年高考江苏物理试卷第9题)如图1所示,倾角为α的等腰三角形斜面固定在水平面上,一足够长的轻质绸带跨过斜面的顶端铺放在斜面的两侧,绸带与斜面间无摩擦.现将质量分别为M,m(M>m)的小物块同时轻放在斜面两侧的绸带上.两物块与绸带间的动摩擦因数相等,且最大静摩擦力与滑动摩擦力大小相等.在α角取不同值的情况下,下列说法正确的有
A.两物块所受摩擦力的大小总是相等
B.两物块不可能同时相对绸带静止
C.物块甲不可能相对绸带发生滑动
D.物块乙不可能相对斜面向上滑动

图1
在文献[1]中,作者通过直接比较斜面倾角的tanα与动摩擦因数μ的大小关系来判断物块的运动情况,对物块运动的描述为:
(1)当α 笔者认为作者通过直接套用单个物块在斜面上滑动的临界条件tanα与μ的关系来判断此题中两物块的运动情况值得商榷.此题为连接体问题,发生相对滑动的临界条件需通过计算、分析才能知晓,为此,笔者通过对物体运动过程的假设,运用牛顿第二定律列式求解,再结合发生相对滑动的临界条件对此题进行分析. 假设两物块相对轻质绸带静止,以大小相等的加速度沿斜面加速运动. 如图2所示,对两物块进行受力分析,绸带对物块的摩擦力均为静摩擦力,应用牛顿第二定律对系统列式 Mgsinα-mgsinα=(M+m)a 图2 求得系统的加速度为 对物块甲分析 Mgsinα-f1=Ma 解得 若使物块甲与绸带保持相对静止,需要求f1<μMgcosα,得出 对物块乙分析 f2-mgsinα=ma 解得 物块乙与绸带相对静止,需要求 f2<μmgcosα 得出 (1)两物块均相对绸带发生滑动 物块甲和物块乙对绸带的摩擦力均为滑动摩擦力 f1=μMgcosαf2=μmgcosα 可得 f1>f2 轻质绸带沿绸带方向所受合力 F=f1-f2>0 轻质绸带的质量m0=0,则轻质绸带的加速度 得出轻质绸带比两物块都要运动得快的谬论,故此.假设的运动过程不存在.因此,可得物块甲不可能相对绸带发生滑动. (2)物块甲相对绸带静止与绸带一起加速下滑,物块乙相对绸带发生滑动 物块甲与绸带间的摩擦力为静摩擦力f1,物块乙与绸带的摩擦力为滑动摩擦力 f2=μmgcosα 要求绸带沿绸带方向合力为零,可得 f1=f2=μmgcosαf1<μMgcosα 故此种运动情况存在. 对物块甲与绸带列式 Mgsinα-μmgcosα=Ma甲 得物块甲与绸带的加速度为 对物块乙列式 μmgcosα-mgsinα=ma乙 得物块乙的加速度为 a乙=μgcosα-gsinα 若物块乙相对斜面加速上滑,则应有 a乙=μgcosα-gsinα>0 得 tanα<μ 若物块乙相对斜面加速下滑,则应有 a乙=μgcosα-gsinα<0 得 tanα>μ 若物块乙相对斜面静止,则应有 a乙=μgcosα-gsinα=0 得 tanα=μ 此时,物块甲的加速度为 综上分析,应用求出的临界条件对两物块的运动过程的准确描述为: 物块乙相对绸带发生滑动且沿斜面加速上滑,加速度为 a乙=μgcosα-gsinα (3)当tanα=μ时,物块甲相对绸带静止一起沿斜面加速下滑,加速度为 物块乙相对绸带发生滑动且相对斜面静止. (4)当tanα>μ时,物块甲相对绸带静止一起沿斜面加速下滑,加速度为 物块乙相对绸带发生滑动且沿斜面加速下滑,加速度 a乙=gsinα-μgcosα 参考文献 1 吴畅.2011年高考江苏物理试卷第9题探析.物理通报,2012(5):126

2 临界条件及运动过程的分析
2.1 临界条件



2.2 当时两物块的运动情况




3 运动过程的准确描述