数字电感转换器的一种自适应数据拟合方法

（西安邮电大学 通信与信息工程学院，西安 710061）

数字电感转换器（以下简称传感器）是一种新型的电涡流传感器，其输入值为导体相对线圈的位移量x，输出值为线圈系统的并联谐振阻抗的变化值经传感器内置模数转换模块转化而来的数字量y。传感器的输出值因与导体相对线圈的位移量的不同而不同，可以表示为位移量x的一元多项式，并采用多项式回归[1]来建立数学模型。

为了获得模型系数，典型的做法是在确定了多项式的阶数后采用最小二乘法求出系数[2]。然而，模型阶数的选择却没有一个很好的解析方法。从理论上说，阶数越高，得到的拟合曲线越完美。但是，如果多项式的阶数过高，虽然拟合效果好，但由于高阶多项式Runge现象[3]的存在，导致拟合后的曲线不能很好地反映数据点变化的统计规律，对于新的观测点而言，它的预测功能就会变弱。而阶数选择过小，则会影响拟合效果。因此采用多项式模型进行数据拟合[4-6]时存在一个合理选择阶数的问题。

有人提出自适应最小二乘法来确定模型阶数[7]，求解多项式系数。用最小二乘法求解系数是假设样本的自变量是非随机的，而样本因变量y由于受到随机扰动量的影响而随机波动，即认为散点之所以偏离线性方程完全是因为散点在因变量的方向上下波动而不是由于在自变量和因变量2个方向上波动所共同造成的。鉴于此，提出一种基于几何距离准则[8-9]下的自适应数据拟合方法求取散点的最佳拟合曲线。

1 几何距离准则下的自适应数据拟合

1.1 几何距离准则

假定传感器测量数据组（x，y）所满足的n阶多项式的模型形式为

令 x1=x，x2=x2，…，xn=xn，则式（1）可变为以下超平面：

对数据组（x，y）拟合的实际问题变为在n维空间中采用以上超平面进行拟合数据。采用超平面的选择标准为数据到超平面的距离平方和最小。

定义数据点到超平面的距离：

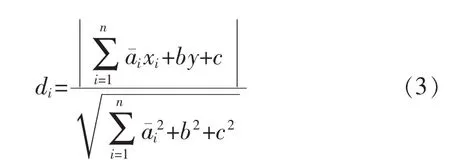
为数据点到超平面的几何距离。

定义数据拟合的评价函数：

称min J为几何距离和最小准则，简称为几何距离准则。

1.2 算法步骤

采用多项式进行数据拟合前，为了使测量数据不影响拟合曲线的特性，在拟合前需对测量数 据进行重构。 设数据对为原始数据（xi，yi）经过重构后的数据，其中i=1，2，…，N。

1.2.1 算法思路

对于给定n阶多项式模型，先在几何距离准则下求取模型参数，文献[5]给出了在几何距离准则下求取模型参数的方法，这里不再赘述。对得到的拟合数据进行自适应迭代，当迭代达到一定次数时，计算拟合数据与原始数据的RMS值，RMS越小，拟合数据与原始数据越接近，拟合效果越好[10]。逐阶执行这一过程。选择RMS最小时的n作为数据的最佳拟合曲线的阶数。实际中，高阶多项式不稳定，所以此算法中n的取值在2～10之间。综合以上思路，给出算法基本流程如图1所示。

图1 算法流程Fig 1 Flow chart of algorithm

1.2.2 自适应过程

2 仿真实验

2.1 数据采集

根据传感器工作原理可知，位移量的变化引起传感器中并联谐振阻抗变化，这种变化经过传感器自带的LDC1000模数转换后保存在寄存器中。本次数据采集设定传感器线圈为默认线圈，由于传感器可感应的最大感应距离为传感器线圈的直径，因此设定导体相对线圈位移量变化范围为0～3 mm，每次测量调整位移间隔量为0.1 mm，记录软件显示稳定时的y值。来回反复测量50组，取平均值后记录如表1所示。

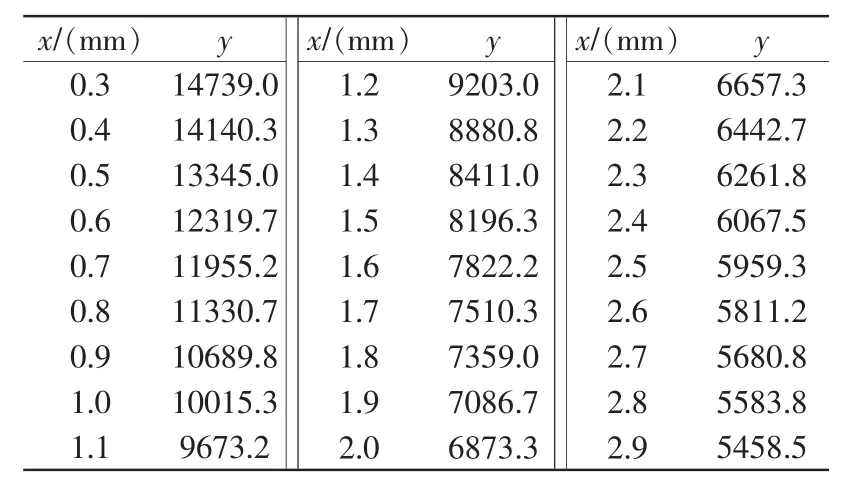
表1 测量数据的平均值Tab.1 Average of the measurement data

表1中，x为导体相对线圈的位移量，单位mm；y为传感器稳定后对线圈系统的并联谐振阻抗经模数转换后的显示值，无量纲。传感导体材料为铁，形状为顶面螺旋上升的柱体。受趋肤效应的影响，导体在感应点x=0.0 mm、0.1 mm、0.2 mm及3.0 mm 4个点处所记录的数据误差比较大，该误差为实际误差，为了数据的可靠性，剔除这4个位移量的测量数据。其余所给出的测量数据为可靠数据，可用于数据拟合。

2.2 算法仿真

算法仿真基于Matlab软件仿真平台，选取参量T 分别为 1，10，40，70，100， 多项式次数 n 取 2～10。仿真结果如表2所示。

表2中，实际仿真程序采用了2～10次多项式拟合。其中n=7，9，10的情况，不符合拟合条件，故认为数据不适合采用该多项式拟合，故未列出。分析 n=2，3，4，5，6，8 时的情况，除了在 T=1 时，n=2 时RMS值比n=3时RMS值小，其余情况均为n=3时RMS最小。可以认为3次多项式拟合曲线为数据的最佳拟合曲线。

表2 T值与n值不同时拟合数据与测量数据的RMS值Tab.2 RMS value between fifting data and measurement data when T and n is diffent

为进一步分析3次多项式对数据的拟合效果，给出在n=3时不同的迭代次数下拟合曲线图 （图2），以及迭代100次时，拟合曲线与原始数据的RMS值的变化图（图3）。

图2 n=3时，不同的迭代次数下的拟合曲线Fig.2 Fitting curve when n=3 and T is different

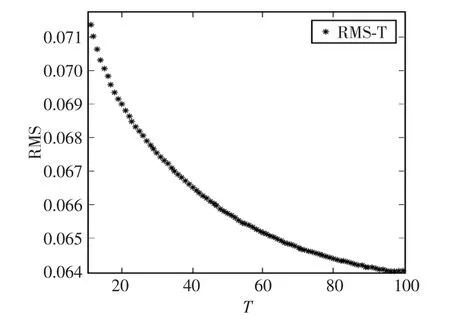
图3 n=3 T=100时的RMS散点Fig.3 When n=3 T=100 RMS scatter plot

通过图3可以看出，随着迭代次数的增加拟合曲线与原始曲线的RMS值不断的变小，当在T=100左右的时候，基本趋近于平稳。这种变化在图2中随着迭代的增加，拟合曲线与原始数据逐步逼近趋势相一致。图2和图3充分验证了该算法的可行性，证明了该算法所得到的多项式拟合曲线为最优拟合曲线。

3 结语

本文提出了在几何距离平方和最小准则下自适应数据拟合方法对传感器静态标定数据对进行散点拟合，通过仿真验证，该算法合理可行，具有较快的收敛速度。

[1]Rajan A，Ye Chow Kuang Ooi，MP-L.Standard uncertainty estimation on polynomial regression model[J].Sensors Applications Symposium（SAS），2014：207-212.

[2]王桂增，叶昊.主元分析与偏最小二乘法[M].北京：清华大学出版社，2012.

[3]Chen Yiqing.High-order polynomial interpolation based on the interpolation center's neighborhood the amendment to the runge phenomenon[J].Software Engineering，2009（2）：345-348.

[4]郑文.曲线拟合[D].重庆：西南大学，2008.

[5]刘海香.散乱数据点曲线拟合的研究及二次曲线拟合的一种新方法[D].济南：山东大学，2005.

[6]刘俊.移动最小二乘散点曲线曲面拟合与插值的研究[D].杭州：浙江大学，2011.

[7]李蓓蕾.多次自适应最小二乘曲线拟合方法及其应用[D].荆州：长江大学，2014.

[8]牛常胜，杨国为，廖福成，等，基于几何距离准则的新数据拟合方法[J].微计算机信息，2006，22（24）：151-152.

[9]朱文华，覃爱丽.基于几何距离准则拟合铁路线路参数的研究[J].铁路计算机应用，2010，19（5）：14-16.

[10]郭金海，杨锦伟.GM（1，1）模型初始条件和初始点的优化[J].系统工程理论与实践，2015，11（9）：2333-2338.