基于HCS-GNN模型的ORP传感器故障诊断

（新疆大学 电气工程学院，乌鲁木齐 830047）

生物氧化预处理过程是生物氧化提金工艺中的重要环节，而氧化还原电位ORP（oxidation reduction potential）传感器是生物氧化预处理过程检测系统中最重要的组成部分，其输出值直接反映当前矿浆的氧化程度。ORP传感器工作在强酸且高密度的溶液中，经常会发生恒增益、恒偏差、显著突变等故障，若不及时解决这些问题，会直接影响工艺最终提金率。因此，研究ORP传感器的故障诊断具有重要意义。

由于生物氧化预处理过程各因素之间存在复杂的非线性关系，并具有不确定性，实际中能够用于测量ORP的各种信息也很贫乏[1]，所以本文选用混合布谷鸟搜索算法优化灰色神经网络HCS-GNN（hybrid cuckoo search-grey neural network） 预测模型对ORP传感器进行故障诊断。灰色神经网络具有灰色模型能够分析贫信息、小样本数据的特点，也具有神经网络的自学习、逼近任意非线性函数的能力[2]。但也存在固有缺陷，比如其权值和阈值在初始化过程中有很大的随机性，网络容易陷入局部最优。针对上述灰色神经网络存在的问题，本文提出了一种混合布谷鸟优化算法，该算法将教与学优化算法中的学习机制同2种变异策略引入到基本布谷鸟搜索算法CSA（cuckoo search algorithm）中，以克服布谷鸟算法寻优速度慢及精度低的缺点，进而建立基于HCS-GNN的ORP传感器预测模型，并应用于ORP传感器故障诊断。

1 灰色神经网络

设原始数据序列为

经过累加生成以指数增长的数据序列X（1），记X（0）为 x（t），X（1）为 y（t），其预测结果用 z（t）表示。 则由n个参数组成的灰色神经网络预测模型的微分方程可表示为

式中：y2，…，yn为输入参数；y1为输出参数；a，b1，…，bn-1为微分方程的系数。

式（1）的时间响应式可表示为

则预测结果为

将式（3）映射到一个BP神经网络中，就得到一个具有n个输入，1个输出的灰色神经网络[2]，其网络拓扑结构如图1所示。

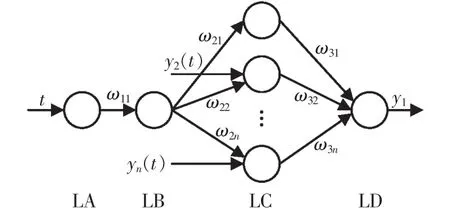
图1 灰色神经网络拓扑结构Fig.1 Gray neural network topology

图中：t为输入参数序号；y2（t），…，yn（t）为神经网络输入；ωij为各层输入的网络权值；y1为模型预测值；LA，LB，LC，LD为灰色神经网络的4层。其网络输出为

2 混合布谷鸟优化算法

2.1 基本布谷鸟算法

布谷鸟搜索算法[3-6]是一种群智能优化算法。其主要灵感源于布谷鸟繁殖后代的行为与Lévy飞行的模式。布谷鸟繁殖后代时会将自己的卵放置于其他鸟类的巢穴中，让其代为孵化。而鸟巢主人若发现鸟巢中有非自己的卵，将会放弃孵化甚至放弃整个鸟巢。为了更简洁方便地描述CS算法，需要作出如下3种理想假设：

1）每只布谷鸟1次只产1个卵，并随机寻找其他的鸟巢来孵化；

2）在随机选择的1组鸟巢中，最好的鸟巢会保留至下一代；

3）可供利用的鸟巢的数量n是固定的，并且鸟巢主人发现外来卵的概率为Pa∈［0，1］。

通过以上3种理想状态下的假设，布谷鸟寻优过程中每个解的位置及路径的更新公式可以表示为

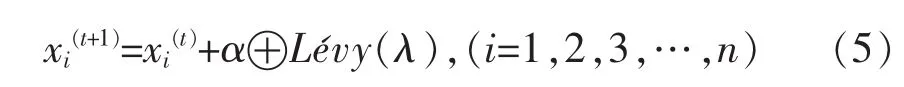
算法中，每一个鸟巢就被看作是一个解，程序初始化过程中，每个解的位置都是随机的。此外，一部分差的鸟巢会以Pa概率被抛弃，而新的鸟巢又会通过式（5）在新的位置建立。位置更新之后，用随机数 r∈［0，1］与 Pa进行对比，若 r＞Pa，则对 xi（t+1）进行随机改变，反之则不变，其中Pa一般设置为0.25。文献[3]对式（5）进行了详细的研究，将其概括为

式中，u和v服从正态分布，即：

2.2 CS算法的改进策略

基本CS算法具有参数少、操作简单、容易实现等优点，但由于CS算法采用Lévy飞行的机制进行搜索，具有一定的盲目性，会导致算法在搜索后期产生无效迭代。因此，该算法存在收敛速度低及寻优精度不高的缺陷。本文受教与学优化算法的启发，首先，把互相学习机制引入到CS算法中，以增强算法的局部搜索能力，并加快算法收敛速度；另外，引入2种新的变异策略，以增加种群的多样性，均衡算法的聚集与发散，从而提高算法的寻优精度。

2.2.1 互相学习机制

为了更好地提高布谷鸟算法的寻优能力，受教与学优化算法的启发，把教与学优化算法的学习机制引入到该算法中。在布谷鸟寻找鸟巢的过程中，也要分析各个相邻鸟巢之间的好的位置信息，以便找到更好位置的鸟巢，因此，各个鸟巢之间互相交换信息、互相学习，假设所优化的问题是最小值问题，其互相交换信息的表达式为

式中，Xr1和Xr2是种群中不同于Xold的随机选择的2个不同个体。

2.2.2 两种变异策略

基本的CS算法虽不易于陷入局部最优，但算法搜索具有一定的盲目性，会使算法的搜索效率降低。为了更好地均衡算法的全局勘探能力和局部开发能力，使算法向着全局最优解的方向搜索，同时增加种群多样性，引入2种变异策略：

式中：Xkj和Xbj为种群中不同于Xij的2个随机个体；Xbest，j为种群中具有最优位置的鸟巢；ζ为扰动步长。

2.3 改进布谷鸟搜索算法优化灰色神经网络的步骤

在灰色神经网络中引进HCS优化算法的目的是为了优化 GNN 的白化参数 a 和 bi（i=1，2，…，n-1）。本文将训练样本个体预测值与实际值之间的残差作为HCS的适应度值，经有限次迭代后，得到最优个体，并将该个体的值作为灰色神经网络的初始权值。其具体实现步骤如下：

步骤1采用式（11）对初始数据进行归一化处理，并对各维数据进行一次累加：

式中：Xi，j代表样本值的第 i行 j列原始数据；xmax代表最大值；xmin代表最小值。

(3)梁弯曲挠度分布在裂纹处存在尖点,且对于开裂纹,当载荷较小时,挠度在裂缝处的尖点现象并不明显,但随着载荷的增加,尖点现象愈加明显.同时,梁横截面转角在裂纹处发生突变,转角不连续.

步骤2参数初始化，确定HCS算法的种群规模P，发现概率Pa，最大迭代次数nIter，问题维数nd，独立运行次数 G，搜索空间范围［Ub，Lb］。

步骤3适应度值计算，根据样本数据确定灰色神经网络结构，待优化参数 a和 bi（i=1，2，…，n-1），并确定个体编码方式，采用式（12）计算个体适应度值fitnessi：

式中：n为测试样本数量；m为输出数据个数；yij为第j个节点的期望输出；tij为相应节点的实际输出。

步骤4利用Lévy飞行搜索的式（7）对鸟巢位置进行更新，产生一组新的鸟巢位置。计算其适应度值，并将其与游走前鸟巢位置的适应度值相比较，保留较优的鸟巢位置。

步骤5互相学习过程，经过Lévy飞行游走之后，个体之间按式（8）进行随机的交流和学习，比较学习前后的个体，并保留较优的个体。

步骤6变异操作，生成一个随机数rand，将其与概率Pa比较，若rand＜Pa，则保留该鸟巢位置。利用式（9）和式（10）对种群进行变异操作，以产生一组新的鸟巢位置，将新的鸟巢位置与被发现前鸟巢位置进行比较，并保留较好的鸟巢位置。

步骤7判断是否满足终止条件，若不满足，继续循环执行步骤2到步骤6，若满足，则终止迭代过程。

步骤8将迭代完成后得到最优位置的鸟巢作为灰色神经网络白化方程的参数a和bi（i=1，2，…，n-1），按照灰色神经网络的权值训练方法进行网络训练，不断调整权值和阈值，判断是否到达训练次数，若满足要求则终止迭代。

3 基于HCS-GNN的ORP传感器输出预测模型的仿真分析

生物氧化预处理过程中氧化还原电位ORP的值是在温度、pH、进风量、矿浆浓度等因素相互作用下的结果，且ORP的值与这些因素之间均呈现高度非线性的关系。因此需要对上述因素综合考虑以实现对ORP值的高精度预测。

在实际工程中矿浆浓度等因素为定值，因此本文选择温度、pH值及进风量作为灰色神经网络的输入变量，以ORP的值作为灰色神经网络的输出变量，并根据所提出的算法进行仿真。

实验以新疆某金矿的实际生产数据进行仿真研究，经筛选后，取其中65组进行灰色神经网络的建模。其中前45组数据作为训练样本，后20组数据作为测试样本。

将HCS-GNN预测模型分别与CS-GNN和GNN模型进行对比，并采用平均绝对误差MAE（mean absolute error）与均方根误差 RMSE （root mean square error）指标对预测效果进行检验，其比较结果如表1所示，结果显示HCS-GNN模型对ORP传感器的输出值具有更优秀的预测能力。HCS-GNN模型的预测结果如图2所示。

式中：N为样本对数；yi*为第i组样本作用下的期望输出；yi为第i组样本作用下的实际输出。

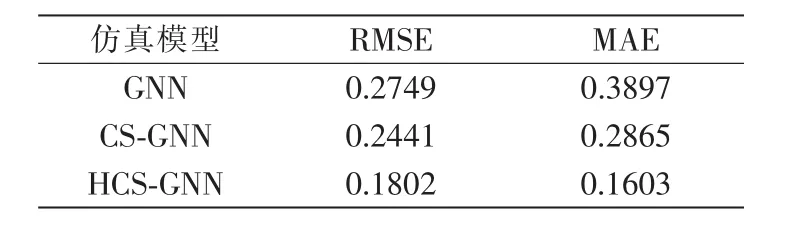
表1 不同方法的预测结果比较Tab.1 Comparison of the prediction results of different methods

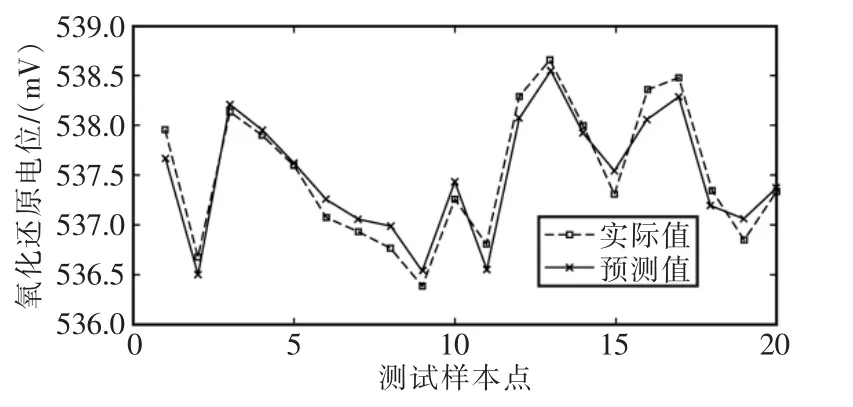
图2 HCS-GNN算法的ORP值预测结果Fig.2 Prediction results of ORP value by HCS-GNN algorithm

4 基于HCS-GNN的ORP传感器输出预测模型故障诊断实现

基于HCS-GNN的ORP传感器故障诊断模型如图3所示，将实际生产中测得的温度、pH值、进风量参数值作为模型的输入，得到 ORP的高精度预测值y1*，将其与当前时刻ORP传感器实际输出值y1进行比较，得到残差σ，设定故障阈值ε为6。若残差σ绝对值大于设定的阈值ε，即则判定ORP传感器发生故障；若则判定ORP传感器工作正常。

图3 ORP传感器故障诊断模型Fig.3 Fault diagnosis model for ORP sensor

若ORP传感器处于正常工作状态，则其模型预测值y1*与实际输出值y1所形成的残差变化很小，均值近似为零，即如图4（a）所示。若在某时刻ORP传感器出现恒增益故障，模型预测值y1*与实际输出值y1所形成的残差将超过阈值，且差信号近似为y（t）= βx（t）（β 为增益比例系数），如图 4（b）所示。若在某时刻ORP传感器出现恒偏差故障，模型预测值y1*与实际输出值y1所形成的残差信号近似为y（t）=x（t）+Δ，即出现值为 Δ 的恒偏差，如图 4（c）所示。若在某时刻ORP传感器出现显著突变故障，模型预测值y1*与实际输出值y1所形成的残差信号将在某一短时间内严重超过阈值，如图4（d）所示。

图4 ORP传感器在4种状态下残差的变化曲线Fig.4 Change curve of ORP sensor in 4 states

当ORP传感器出现恒增益、恒偏差及显著突变故障时，其由模型预测值与传感器实际输出值得到的残差将大于设定的阈值，此时则判定传感器发生了故障，诊断系统立刻报警。

5 结语

本文提出一种HCS与灰色神经网络相结合的ORP传感器故障诊断方法。在HCS-GNN预测模型的设计中，采用HCS算法优化灰色神经网络，克服了基本CS算法收敛速度慢和寻优精度低等缺点，并构建了基于HCS-GNN的ORP传感器预测模型。利用生物氧化预处理过程中采集的数据集进行训练并测试了HCS-GNN模型的性能，预测结果表明该模型的预测精度要明显优于CS-GNN模型与传统GNN模型。将该预测模型应用到ORP传感器故障诊断中，仿真结果表明本文提出的故障诊断方法能够快速且有效地诊断出ORP传感器常出现的恒增益、恒偏差、显著突变故障，从而确保了ORP传感器工作的可靠性，而且降低了维护成本，在生物氧化预处理过程中有较高的应用价值，同时也为其他工业生产中传感器故障诊断提供了一种新的故障诊断方法。

[1]李伟，南新元，吴琼.生物氧化提金中基于PSO-LSSVM的氧化还原点位建模研究[J].贵金属，2014，35（4）：60-64.

[2]葛少云，贾鸥莎，刘洪.基于遗传灰色神经网络模型的实时电价条件下短期电力负荷预测[J].电网技术，2012，36（1）：224-229.

[3]Yang X S，Deb S.Cuckoo search via levy flights[C]//Proceedings of World Congress on Nature & Biologically Inspired Computing，India：IEEE Publication，2009：210-214.

[4]AmirHossein Gandomi，YangXinshe，AmirHossein Alavi.Cuckoo search algorithm：a metaheuristic approach to structural optimization problems[J].Engineering with Computers，2013（29）：17-35.

[5]Ding Xueming，Xu Zhenkai，Ngaam J Cheung，et al.Parameter estimation oftakagi-suge-no fuzzy systemusing heterogeneous cuckoo search algorithm[J].Neurocomputing，2015 （151）：1332-1342.

[6]Li Xiangtao，Yin Minghao.Modified cuckoo search algorithm with self adaptive parameter method[J].Information Sciences，2015（298）：80-97.