改进型自抗扰算法在焙烧炉温控系统的应用

王 艳 ，刘 斌 ，司长策

（1.天津复杂系统控制理论与应用重点实验室，天津 300384；2.天津理工大学 自动化系，天津 300384；3.天津市斯科诺热能技术有限公司，天津 300384）

在早期的焙烧炉温度控制系统中，对其温度的控制完全依赖于工人的经验，系统没有构成闭环，无法实现自动控温。其电器控制也采用继电器控制技术，其硬件连线固定，给设备的改造和制造带来不便。随着时代的不断发展和科技的不断进步，许多先进的技术应用到了现代工业生产当中。其中计算机技术的发展取代了原来的继电器控制技术，一些基于计算机技术的智能控制器的出现，将智能控制算法写到智能控制器当中，使温度控制系统构成闭环的控制回路，可以实现系统温度自动调节[1]。

本文以双曲正切函数为基础，构造自抗扰控制器中的扩张状态观测器。同时，实现了自抗扰控制算法在温度控制当中的应用。

1 焙烧炉参数及控制系统组成

1.1 焙烧炉参数

根据青岛某车辆厂工艺要求，设计焙烧炉的工艺参数，如表1所示。

表1 焙烧炉工艺参数表Tab.1 Furnace parameter list

炉膛共分为5个温度区，每一个温度区安装有1台双支热电偶和2台烧嘴。每2台烧嘴控制一个温度区，每2个温度区之间是相互独立单独控制且每2个烧嘴相互交错，确保炉膛温度的均匀性。

1.2 焙烧炉控制系统的组成

本控制系统的基本功能：在工控机可以实时、直观地读取炉温信息，具有监控报警功能，同时将控制算法写入到工控机当中，以减少PLC的运算量。采用了先进的自抗扰控制器ADRC（active disturbance rejection controller），使控制精度优于传统的PID控制。本控制系统主要由温度控制、机械运动控制、故障报警与显示等多个子系统构成，如图1所示。

图1 控制系统组成Fig.1 Control system constitute

具体的硬件主要是由传感器、PLC、工控机、其他的执行机构组成。

选用PLC机型为FX2n-64MR，若干数字量输入输出模块和模拟量输入输出模块，将温度信息从检测元件通过模拟量输入模块传送到PLC当中，通过运算指令将温度信息进行标度变换，得到炉膛内的温度，在通过数据线将温度信息传送到工控机，工控机采用自抗扰算法计算出当前的控制量，将控制量回传给PLC，通过运算指令将标度逆变换，通过模拟量输出模块将控制量送到伺服电机，通过伺服电机控制阀的开度来控制炉膛的温度。

2 自抗扰控制器原理与设计

控制就是对被控制对象施加适当的控制力，使其在任何情况下都可以按照期望的方式变化。其施加控制力的方式就是引入希望值与实际值之间的误差信号，对误差信号进行处理，想方设法消除这个误差信号。这就是控制上常说的“基于误差来消除误差”。基于以上的机理，PID控制器为典型的代表，其通过将误差信号的比例、积分和微分环节通过线性加权的方式得到最终的控制量[2]。另外还有“基于内部机理的控制方法”，即从被控对象的数学模型出发来设计系统的控制器。由于基于模型，其建模的准确性直接影响着控制效果。但对于实际的被控对象来讲精确建模是一件很难的事情。所以对控制器的设计应当不完全依赖于数学模型。只有这样才能得到广泛的应用。

自抗扰控制技术最早是由我国系统科学研究院韩京清教授提出的。通过对PID控制器的深入研究，提出了自抗扰控制技术。由于PID控制器只是将信号进行简单的加权，可能不是最优。将其引入非线性函数进行改造，将原有的PID控制器改造成非线性PID控制器，在此基础上与现代控制理论相结合，将系统的内部扰动扩张为新的状态，最终提出了自抗扰控制技术[3]。

自抗扰控制器主要由4部分组成：安排过渡过程（TD）、扩张状态观测器（ESO）、非线性状态误差反馈（NLSEF）、扰动补偿。采用跟踪微分器（TD）根据设定值的大小来合理地安排过渡过程，并且提取微分信号，为获得误差信号做准备；扩张状态观测器（ESO）通过被控对象的输入输出来估计出系统的状态和总扰动，通过TD提取的微分信号与ESO估计出的系统状态来得到误差信号，通过非线性状态误差反馈来得到控制量U0，在通过修正补偿因子b0来得到最终的控制量U。以二阶系统为例，给出系统原理如图2所示。

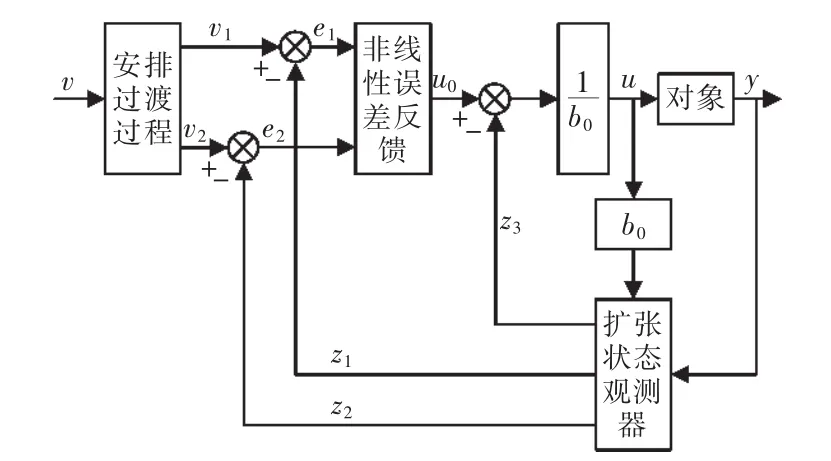
图2 自抗扰控制器原理Fig.2 Principle of active disturbance rejection controller

自抗扰控制器的具体形式为

式中：TD为跟踪微分器；f han（·）为非线性函数；v为系统的输入；r0为跟踪微分的速度因子，其决定着跟踪微分器对输入信号的跟踪速度；h0为滤波因子；扩张状态观测器中的非线性函数选用双曲正切函数搭建而成；z1，z2和z3分别为扩张状态观测器对系统一阶状态、二阶状态和系统的扰动的估计值；β01，β02和β03分别为扩张状态观测器的参数，β01，β02影响对系统一阶状态和二阶状态的估计，β03影响对系统扰动的估计。其参数选择太大时会导致系统不稳定，当选择太小时会使扩张状态观测器跟踪不上原系统各状态。非线性状态误差反馈也采用 fhan（x，y，r，h）非线性函数构建，其中的参数各功能与跟踪微分器相同。其函数的具体表达形式为[4]

3 仿真比较

由于本文自抗扰控制器的扩张状态观测器选用双曲正切函数构造而成。下面进行ESO对二阶系统仿真实验。

设系统为

式中：x1和 x2为系统的状态；y（t）为系统的输出；u（t）为系统的输入；b为系统的一个参数。假设其中非线性扰动为 f（t）=sign（0.5sin（t）），系统的输入为 u（t）=sin（0.5t）。

ESO的参数可以通过极点配置的方法整定[5]。设定参数 β01=20，β02=300，β03=1000 对系统进行仿真实验，如图3、图4所示。

图3 系统二阶状态与估计值Fig.3 Condition and estimate system of second order

图4 系统扰动与估计值Fig.4 System disturbance and estimates

通过图3、图4可以看出2条实线分别为系统的二阶状态和扰动，2条虚线分别为ESO对系统二阶状态和扰动的估计值。在初始时对系统二阶状态和系统扰动的估计值有峰值现象，在后面对于系统的二阶状态可以很好地跟踪，为了抑制这种峰值现象。可以动态地调节ESO的β02和β03的数值[6]。

可以按照式（6），（7）来确定：

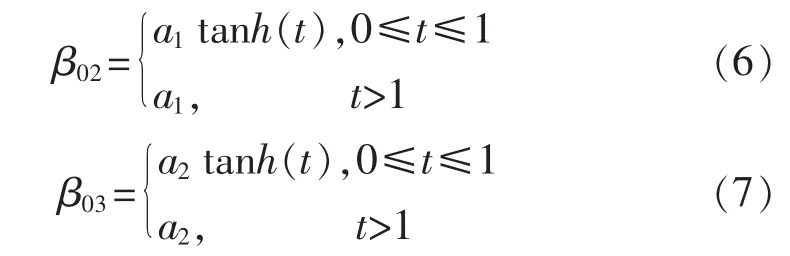
按照上式可以抑制峰值现象，a1，a2为对β02和β03初期的调整参数，仿真中设 a1=a2=200。 b1，b2为对β02和β03后期的调整参数，与系统刚才仿真中β02，β03相等。仿真图如图 5、图 6所示。

图5 采用动态调参后系统二阶状态与估计值Fig.5 Dynamic scheduling using the system and the estimated value of the second-order status

图6 采用动态调参后系统扰动与估计值Fig.6 Dynamic scheduling using system disturbance and estimates

仿真图5中实线为系统的二阶状态，虚线为ESO对系统二阶状态的估计值，可以看出在ESO初期的跟踪系统状态时不会出现峰值。图6中实线为系统的扰动，虚线为ESO对系统扰动的估计值，在估计的初期也没有峰值象限，对于系统的扰动也可以有效地跟踪，说明此方法有效。

4 实验结果

图7为焙烧炉系统实际输出的温度曲线，实线为原有控制算法，虚线为本文所提的控制算法。从图中可以看出在低温段，原控制算法有明显的超调现象；本文算法超调明显降低。当温度上升到200℃以上时2条温度曲线平稳上升，在到达最终温度原控制算法发生了超调，而本文算法没有出现超调现象。后期的温度平稳保持在设定温度±5℃，满足工艺要求，说明该方法有效。

图7 焙烧炉实测温度曲线Fig.7 Measured temperature curve tunnel kiln

5 结语

通过仿真实验验证了基于双曲正切函数的ESO的有效性，并采用动态改变ESO参数的方法抑制了其峰值现象，最后的实验当中进一步验证了采用本ESO建立的自抗扰控制器可以有效地控制炉温。

[1]耿长福.PLC的发展及国产化的进程[J].机械与电子，1995（7）：41-45.

[2]韩京清.自抗扰控制器及其应用[J].控制与决策，1998，13（1）：19-23.

[3]韩京清.从PID技术到“自抗扰控制”技术[J].控制工程，2002，9（3）：13-18.

[4]韩京清.自抗扰控制技术：估计补偿不确定因素的控制技术[M].北京：国防工业出版社，2009.

[5]于希宁，朱丽玲.自抗扰控制器的动态参数整定及其应用[J].华北电力大学学报，2005，32（6）：9-13.

[6]周涛.基于反双曲正弦函数的扩张状态观测器[J].控制与决策，2015，30（5）：943-946.