重物－桥吊耦合系统振动分析

重物-桥吊耦合系统振动分析

谢伟平，黄金，周家玲，何卫

(武汉理工大学土木工程与建筑学院，武汉430070)

摘要：考虑吊重的摆动，将重物-桥吊耦合系统简化为移动质量+吊重在简支梁上运动模型，基于Lagrange方程，推导了移动质量+吊重-简支梁耦合系统运动微分方程。采用Runge-Kutta积分法对微分方程组进行数值求解，分析了移动质量加速度、吊重质量所占比重、吊绳长度等因素对梁体振动响应的影响。数值计算结果表明：对于重物-桥吊耦合系统，若不考虑吊重摆动，采用移动质量过桥模型将会低估梁体振动响应，并且在移动质量与吊重质量之和一定的情况下，吊重质量所占比重越大，梁体的振动响应越大；移动质量加速度对梁体的振动影响不能忽略，尤其是对梁体的加速度响应影响很大。

关键词：重物-桥吊耦合系统；移动质量；吊重；Lagrange方程

中图分类号:TU311.3文献标志码：A

基金项目：国家自然科学基金(51375178);广东省自然科学基金(S2012010008789)资助项目

收稿日期：2014-05-07修改稿收到日期：2014-07-23

Vibration ananlysis of a suspension weight-bridge crane coupled system

XIEWei-ping,HUANGJin,ZHOUJia-ling,HEWei(College of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan 430070, China)

Abstract:Considering the swing of a suspension weight, a suspension weight-bridge crane coupled system was simplified to a model of a mass with a suspension weight both moving on a simply supported beam, and its differential equation of motion was derived based on Lagrange equation. Runge-Kutta numerical integration method was used for numerically solving. Some influence factors on the system vibration response were analyzed, they were acceleration of moving mass, length of wire and ratio of mass of suspension weight to the total mass of the system. The results showed that without considering the swing of the suspension weight, the vibration response of the beam may be underestimated by using the model of the beam subjected to moving masses; when the mass sum of the moving mass and the suspension weight is fixed, the greater the mass of the suspension weight, the larger the vibration response of the beam; the acceleration of the moving mass has a great influence on the beam vibration.

Key words:suspension weight-bridge crane coupled system; moving mass; suspension weight; Lagrange equation

桥式起重机械的载重运行是一类重物-桥吊耦合系统，该系统往往可简化为移动荷载-梁耦合系统。目前，国内外对移动荷载-梁耦合系统做了大量的研究[1-9]。Fryba[1]对移动荷载-梁耦合系统列出了许多建模和分析方法，并研究了梁体动挠度的主要影响因素；彭献[3]对移动质量模型通过简支梁时, 移动质量加减速对桥梁跨中挠度的影响进行了研究；夏禾[4]采用移动簧上质量模型, 分析了簧上质量加减速对桥梁跨中动挠度的影响并进行了共振研究；杨国来[5]采用有限元法和振型叠加法相结合的方法对该系统进行建模，分析了具有大质量、高速度移动载荷下梁体响应问题。

上述分析模型多针对车-桥耦合系统或者弹-炮耦合系统等，对于重物-桥吊耦合系统，重物在起吊运行过程中往往会发生摆动，此时上述分析模型不再适用。关于重物-桥吊耦合系统的振动分析，国内外鲜有文献报道。本文考虑吊重的摆动，将重物-桥吊耦合系统简化为移动质量+吊重在简支梁上运动模型，基于Lagrange方程，推导了移动质量+吊重-简支梁耦合系统运动微分方程。采用Runge-Kutta积分法对运动微分方程组进行了数值求解，分析了移动质量加速度、吊重质量所占比重、吊绳长度等因素对梁体振动响应的影响。

1耦合系统运动微分方程的建立

移动质量+吊重-简支梁耦合系统如图1所示。

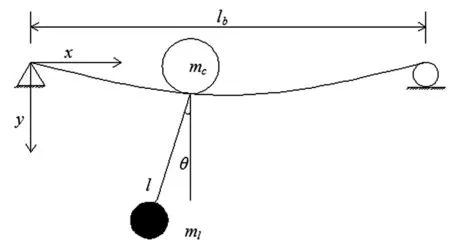
图1　移动质量+吊重-简支梁耦合系统模型 Fig.1 The model of the moving mass andthe suspension weigh moving on the simply supported beam

假设简支梁为Euler-Bernoulli梁，梁体阻尼对结构振动影响很小[2]，不考虑梁体阻尼；为了简化分析，根据桥式起重机械载重运行的实际工作情况，吊绳假设为无质量刚性吊绳[10]；吊重简化为一个摆动的集中质量，通过无质量的刚性吊绳悬挂在质量块上，随着质量块一起运动并且在平面内摆动。

梁单元坐标可用式(1)表示

xb=x

(1)

小车坐标可用式(2)表示

xc=xc(t)

(2)

吊重坐标可用式(3)表示

xl=xc+lsinθ

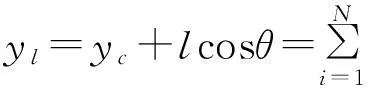
(3)

系统的总动能可用式(4)表示

(4)

系统的总势能可用式(5)表示

(5)

(1)对广义坐标qj应用Lagrange方程得式(6)

(6)

(2)对广义坐标θ应用Lagrange方程得式(7)

(7)

式(6)、(7)联立，该系统的运动微分方程组如式(8)所示。

(8)

2耦合系统振动响应的求解

由式(8)可知，系统的运动微分方程是(N+1)元二阶非线性时变微分方程组，该微分方程组的非线性和时变特性给求解带来了一定的难度。本文采用Runge-Kutta积分法自主编程求解，在程序编制过程中为了方便程序编制，将时变量xc作为一个已知响应的自由度，本文称为“定位自由度”。“定位自由度”与其它自由度之间是非线性耦合的，这时方程组多了一个自由度，如式(9)所示，此时系统运动微分方程为(N+2)元二阶非线性微分方程组。

(9)

2.1计算模型的验证

为了验证本文计算模型的正确性，选取文献[3]中的计算实例进行求解。取N=8；吊重质量ml为0，此时本文模型退化为文献[3]中移动质量块过桥模型。相关计算参数如表1所示，计算结果对比如图2所示。通过对比可知本文计算结果与文献[3]采用New-mark方法计算的结果非常吻合，从而验证了本文计算模型的正确性。

表1　计算参数

图2　本文与文献[3]计算结果对比图 Fig.2 Comparison of literature [3] and this paper

2.2耦合系统振动响应求解分析

为了与移动质量过桥模型进行比较，假定移动质量与吊重质量之和一定，定义吊重质量所占比重r为吊重质量与移动质量之比，即r=ml/mc；吊绳长度l与梁跨度lb之比为n，即l/lb=n。相关计算参数如表1所示。

移动质量加速度对梁跨中位移的影响如图3所示。虽然本文与文献[3]的分析模型不同，但由图3可得到与文献[3]相一致的结论，即在同一初速度情况下，移动质量的加速度越大，梁跨中的挠度越大。其力学解释文献[3]已给出，本文不再赘述。

移动质量加速度对梁跨中加速度影响如图4所示。由图可知，移动质量的加速度越大，梁跨中的加速度越大，这种影响在移动质量初速度较低的情况下表现得尤为明显。

图3　移动质量加速度对梁跨 中位移的影响(r=1;n=0.05) Fig.3 Effect of acceleration of moving mass on the mid-span deflection (r=1;n=0.05)

在移动质量与吊重质量之和一定时，梁跨中位移最大值和加速度最大值随吊重质量所占比重r变化规律如图5所示。由图可知，①当r=0时，模型退化为移动质量过桥模型，而在区段r∈[0,5]时，梁跨中位移最大值和加速度最大值都随r增大而显著增大。这说明吊重摆动荷载的存在会增大梁体的振动响应，而单纯的移动质量过桥模型会低估吊重摆动荷载对梁体振动响应的影响；②梁跨中位移最大值和加速度最大值都随r增大而增大。这说明移动质量与吊重质量之和一定，吊重质量所占比重越大，梁体的振动响应越大；③移动质量的加速度越大，其变化趋势越明显。这说明移动质量加速度越大，吊重摆动荷载对梁体振动响应的贡献越大。

图4　移动质量加速度对梁跨中 加速度的影响(r=1;n=0.05) Fig.4 Effect of acceleration of moving mass on the mid-span acceleration (r=1;n=0.05)

图5　梁跨中位移最大值和加速度最大值 随r变化规律(n=0.05) Fig.5 The variation of the maximal value of mid-span deflection and acceleration with the mass ratio of the suspension weigh (n=0.05)

图6　梁跨中位移最大值和加速度最大值随 n和r变化规律(v 0=10 m/s;a=1 m/s 2) Fig.6 The variation of the maximal value of mid-span deflection and acceleration with the length of the wire and the mass ratio of the suspension weigh(v 0=10 m/s;a=1 m/s 2)

梁跨中位移最大值和加速度最大值随吊绳长度与梁跨度之比n的变化规律如图6(a)、6(c)所示。由图可知，梁跨中位移最大值和加速度最大值随n增大而增大，当n达到某一值G时，梁跨中位移最大值和加速度最大值随n增大而减小，最后慢慢趋于稳定，说明梁跨中位移最大值和加速度最大值在n=G处存在极大值点。

在移动质量与吊重质量之和一定，吊重质量所占比重r不同时，梁跨中位移最大值和加速度最大值随n变化规律如图6(a)、6(c)所示。由图可知，r并没有改变梁跨中响应随n的变化趋势，只是对其变化幅度有所影响，r越大变化幅度越显著，这也进一步验证了移动质量与吊重质量之和一定时，吊重质量所占比重越大，梁体的振动响应越大这一结论。G值随r的变化规律如图6(b)、6(d)所示。由图可知，吊重质量所占比重r对跨中位移最大值和加速度最大值所对应的G值都没有影响，都为0.036，这也从侧面验证了吊重摆动荷载的频率与吊绳长度有关，而与吊重质量无关。

表2　G值所对应的摆动荷载近似频率与梁体基频关系

通过表2分析可知，G值所对应的吊重摆动荷载近似频率大致是梁体基频的一半，即当吊重摆动荷载的近似频率在梁体基频一半附近时，梁体响应最大，所以可以通过调节吊绳长度，避免其近似频率在梁体基频一半附近。

3结论

本文基于Lagrange方程，推导了移动质量+吊重-简支梁耦合系统运动微分方程。该微分方程组为非线性时变微分方程组，为便于求解采用将时变量作为“定位自由度”的方法，增加了一个已知响应的自由度，采用Runge-Kutta积分法对改变后的运动微分方程组进行了数值求解。通过对不同参数下梁体的振动响应求解分析，可得到以下结论：

(1)对于重物-桥吊耦合系统，若不考虑吊重摆动，采用移动质量过桥模型将会低估梁体振动响应，并且在移动质量与吊重质量之和一定的情况下，吊重质量所占比重越大，梁体振动响应越大。

(2)在移动质量+吊重-简支梁耦合系统模型中，移动质量的加速度越大，梁体振动响应越大且吊重摆动荷载对梁体振动响应的贡献越大。

(3)当吊重摆动荷载的近似频率大致是梁体基频一半时，梁体响应最大，可以通过调节吊绳的长度来改变吊重摆动荷载的频率，避免其近似频率在梁体基频一半附近。

参考文献

[1]Fryba L. Vibration of solids and structures under moving load[M]. Noordhoff International Publishing, Groningen, The Netherlands, 1995.

[2]Michaltsos G T. Dynamic behavior of a single-span beam subjected to loads moving with variable speeds [J]. Journal of Sound and Vibration, 2002, 258(2): 359-372.

[3]彭献, 刘子建, 洪家旺. 匀变速移动质量与简支梁耦合系统的振动分析[J]. 工程力学, 2006, 23(6):25-29.

PENG Xian, LIU Zi-jian, HONG Jia-wang. Vibration analysis of a simply supported beam under moving mass with uniformly variable speeds [J]. Engineering Mechanics, 2006, 23(6):25-29.

[4]王少钦, 夏禾, 郭薇薇，等. 变速移动荷载作用下简支梁桥的动力响应及共振分析[J]. 振动与冲击, 2010, 29(2):26-30.

WANG Shao-qin, XIA He, GUO Wei-wei, et, al. Dynamic response and resonance analyses for a simply supported bridge under speeds varying loads [J]. Journal of Vibration and Shock, 2010, 29(2):26-30.

[5]陈强, 杨国来，王晓峰，等. 变速移动载荷作用下梁的动态响应数值模拟[J]. 南京理工大学学报, 2011, 35(2):204-208.

CHEN Qiang, YANG Guo-lai, WANG Xiao-feng, et, al.Numerical analysis for dynamic response of beams subjected to moving loads with non-uniform motion [J]. Journal of Nanjing University of Science and Technology, 2011, 35(2):204-208.

[6]王颖泽, 张小兵. 变速多移动质量耦合作用下柔性梁系统振动响应分析[J]. 振动与冲击, 2011, 30(8):56-60.

WANG Ying-ze, ZHANG Xiao-bing. Vibration analysis of Flexible beam under the action of multi-moving masses with variable speeds [J]. Journal of Vibration and Shock, 2011, 30(8):56-60.

[7]杨予, 滕念管, 黄醒春, 等. 承受移动均布质量的简支梁振动反应分析[J]. 振动与冲击, 2005, 24(3):19-22.

YANG Yu, TENG Nian-guan, HUANG Xing-chun, et, al. Vibration analysis of a simply supported beam traversed by uniform distributed moving mass [J]. Journal of Vibration and Shock,2005, 24(3):19-22.

[8]盛国刚, 赵冰. 多个移动质量-弹簧-阻尼系统作用下梁的动力特性分析[J]. 振动与冲击, 2003, 22(1):43-46.

SHENG Guo-gang, ZHAO Bing. Dynamic characteristics of elastic beam under a series of moving oscillating loads[J].Journal of Vibration and Shock, 2003, 22(1):43-46.

[9]刘宁, 杨国来. 移动质量作用下轴向运动悬臂梁振动特性分析[J]. 振动与冲击, 2012,31(3):102-105.

LIU Ning, YANG Guo-lai. Vibration property analysis of axially moving cantilever beam considering the effect of moving mass[J]. Journal of Vibration and Shock, 2012, 31(3):102-105.

[10]邹军, 陈志坚. 桥式起重机水平运行及抓斗防摆规律研究[J]. 山东大学学报:自然科学版,1998,33(4):393-397.

ZOU Jun, CHEN Zhi-jian. The research about horizontal moving rule of bridge crane and swing rule of grab[J].Joural of Shandogn University(Natural Science Edition),1998,33(4):393-397.

第一作者耿宇斌男，硕士，1990年8月生

通信作者赵学智男，教授，1970年11月生