非自由场内声场定量重现的L曲线滤波方法

非自由场内声场定量重现的L曲线滤波方法

彭博,郑四发,廖祥凝,连小珉

(清华大学汽车安全与节能国家重点实验室，北京100084)

摘要：研究了非自由场一般房间内利用扬声器阵列进行声场重现的方法。建立了房间内声场重现的系统模型，利用正则化最小二乘法和L曲线法获得了实现声场内多个控制点定量重现的驱动信号频域特性，然后采用L曲线滤波器设计得到了阵列扬声器时域驱动信号。实际汽车噪声的重现结果表明：L曲线滤波方法能够实现扬声器驱动信号功率与声场重现误差之间的平衡，可以在非自由场内实现稳态声场的定量重现。

关键词：声场重现；滤波方法；L曲线方法

中图分类号:TN912.27文献标志码：A

收稿日期：2013-05-08修改稿收到日期：2014-07-30

L-curve-filtering method for sound field reproduction in a general room

PENGBo,ZHENGSi-fa,LIAOXiang-ning,LIANXiao-min(State Key Laboratory of Automotive Safety and Energy Saving, Tsinghua University, Beijing 100084, China)

Abstract:L-curve-filtering method for sound field reproduction in a general room with a loudspeaker array was studied. Firstly, the system model used for the sound field reproduction in a room was established. Then, the regularized least-square method and L-curve method were used to obtain the filtering properties in frequency domain of drive signals of speakers, they reproduced the sound pressures of multiple controlled points quantitatively. Finally, a L-curve-filter was designed to obtain the time domain drive signals of the loudspeaker array. The test results to reproduce a vehicle noise showed that L-curve-filtering method can balance the power of drive signals and the sound field reproduction error to realize the sound field reproduction in a general room.

Key words:sound field reproduction; filtering method; L-curve method

汽车噪声影响到用户的声学舒适性也影响到社会生活环境，低噪声成为各国汽车产品设计目标之一。在此背景下，对汽车噪声进行准确的声品质评价成为低噪声技术的一个必要环节。目前广泛使用的基于人工头采集、耳机回放的声品质评价系统不能够正确反应评价者对低频噪声的主观感受，基于扬声器的室内声场重现成为下一步的解决方案。

几十年来国内外的研究者一直在探索更加有效的声场重现理论和方法。Gerzon[1]第一次尝试采用球谐函数来描述声场，现在发展成了广泛研究的Ambisonics方法[2-5]。该方法将声场表示成球贝塞尔函数和球谐函数叠加的形式，利用“编码”和“解码”两个步骤分别实现原始声场的拟合和扬声器驱动信号的获取[2-3]。Betlehem[4-5]研究了混响场条件下声场重现的Ambisonics方法，4年后又对该方法进行了拓展，进一步提出了混响场条件下的声场方法。但是，Ambisonics方法针对复杂声场的“编码”过程涉及到局部区域内对大量声场数据的采集，需要数量众多的传声器，影响到其可应用性。同时，实现重现的扬声器阵列如果不能布置成规则的形状(如球形)，采用Ambisonics方法时会带来数值计算的不稳定问题和次优解问题[6]。

Miyoshi[7]等首次提出了在一般房间内实现声场重现的逆向滤波方法。该方法以扬声器驱动信号与声场中离散声压点的传递函数为基础，利用传递函数的逆直接进行滤波器的设计。Nelson[8]指出重现整个声场的复杂性，提出了重现声场传播方向的滤波器设计方法。Kirkeby等[9]进一步研究了实现声场中离散点声压控制的逆卷积方法。上述工作均未涉及声场重现定量指标，也未涉及扬声器驱动的实现方法及试验验证，而定量重现是声品质评价的基本要求。

同时扬声器功率受到物理系统的制约，需要考虑扬声器驱动信号功率与重现误差的平衡问题。为了处理引起该问题的病态性，Tikhonov正则化方法广泛的应用在了工程实际中[10-11]。而怎样在考虑扬声器功率限制的同时合理地选择正则化参数是亟需解决的问题。

以研究采用重现的三维声场进行声品质分析为目标，本文针对一般房间内扬声器阵列的声场重现提出了L曲线滤波方法，来平衡扬声器驱动信号功率和重现误差，解决了Ambisonics方法数值求解的不稳定性问题。文章从一般房间内声场重现的系统模型出发，利用最小二乘法和L曲线方法进行L曲线滤波器频域特性的求解，最后完成了L曲线滤波器的设计。对实际汽车车内噪声的重现实验证明了该方法的有效性。

1声场重现的系统模型

在一般房间内进行声场重现时，通过房间内布置的多个扬声器放音，实现目标区域的声压重现。房间内传播的声波受到了房间边界的反射和吸收，同时房间内存在着聆听者，在聆听者处也会发生反射、衍射等现象。

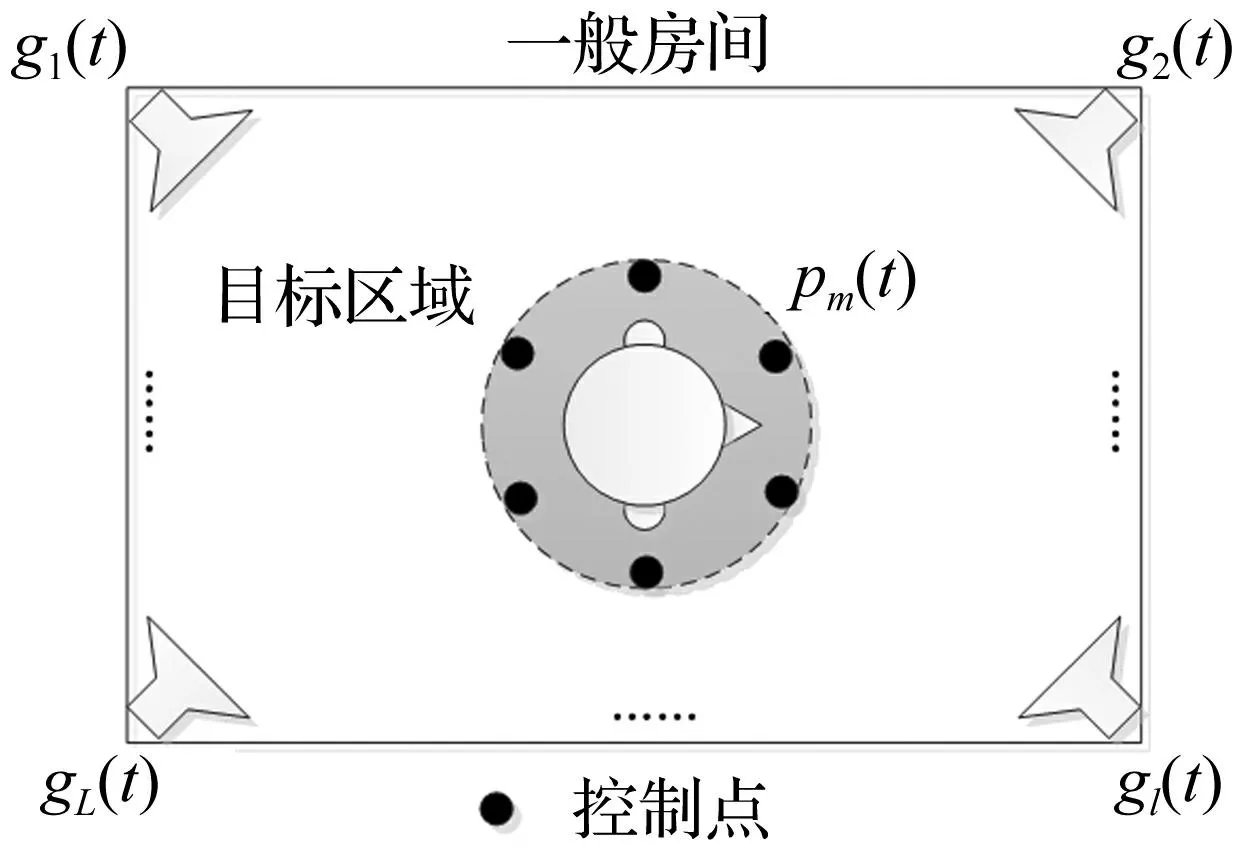
图1　一般房间内声场重现系统模型 Fig.1 System model of sound field reproduction in a general room

如图1为一般房间内声场重现系统模型，目标区域中的人工头模型计入了聆听者对声场的影响，声场重现通过控制目标区域中多个控制点处的声压实现。声场重现系统的控制框图如图2所示。

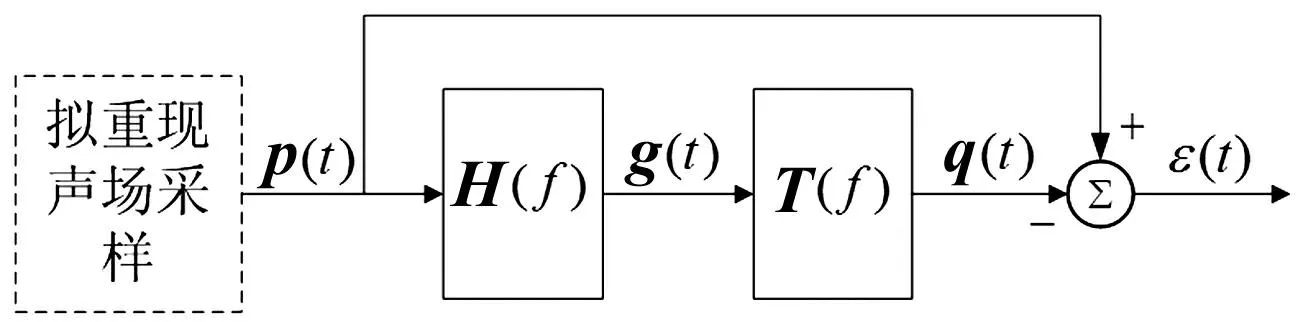
图2　声场重现系统框图 Fig.2 System diagram of sound field reproduction

图中，p(t)=[p1(t),p2(t),…,pM(t)]为原始声场中控制点处的声压信号，M为控制点的数量；g(t)=[g1(t),g2(t),…,gL(t)]为房间内扬声器的驱动信号，L为扬声器的数量；q(t)=[q1(t),q2(t),…,qM(t)]为重现声场中M个控制点处的声压信号；ε(t)为重现误差。H(f)为L曲线滤波系统，T(f)为房间内的电声传递函数矩阵。声场重现的时域声压级误差可用(1)式表达：

(1)

式中，pie(t)和qie(t)表示pi(t)和qi(t)对应的有效声压。在房间内的声场重现系统中，第l个扬声器的驱动信号gl(t)与第m个控制点的声压pm(t)之间的传递关系可由式(2)表示：

Pm(f)=Tml(f)Gl(f)

(2)

式中，Pm(f)和Gl(f)分别为pm(t)和gl(t)的复振幅，f为频率，Tml(f)为它们之间的传递函数。传递函数的取值与房间边界和聆听者对声场的影响相关，房间边界对声波的反射和吸收以及聆听者对声波的反射和衍射效应包含在传递函数中。对于某一特定房间，边界和聆听者确定后，特定扬声器驱动信号和特定传声器之间的传递函数也就唯一确定了。在模型中，人工头模型用于模拟大多数聆听者对声场的影响。

声场重现模型利用M个控制点对声场进行控制，控制点布置成三维的环形包络面，其密度决定了声场重现的最高频率。根据空间采样定理的要求，重现的最高频率可表示为fH=c/(2Δ)，其中c为声速，Δ为控制点的间距。在控制点密度满足最高频率的要求之后，密度的增大并不会带来重现误差的明显减小[8]，因此实际控制点布置的密度满足最高频率即可。

声场重现的系统模型利用L个扬声器放音，通过M个控制点对声场进行控制，该过程可表示为：

P(f)=G(f)T(f)

(3)

式中，P(f)=[P1(f),P2(f),…,PM(f)]为M个控制点声压的复振幅，G(f)=[G1(f),G2(f),…,GL(f)]为L个扬声器驱动信号的复振幅，T(f)为L个扬声器驱动信号到M个控制点声压的传递函数矩阵，定义为：

(4)

2L曲线滤波的声场重现方法

2.1L曲线滤波器的频域特性

在一般矩形房间中进行声场重现声场时，扬声器阵列布置受房间空间限制，不满足规则的球形或半球形形状，同时扬声器的数量、扬声器驱动信号功率也受到限制，因此利用式(3)求解扬声器驱动信号时，为了得到稳定的驱动信号，构造约束条件下扬声器驱动信号的最小二乘解如下：

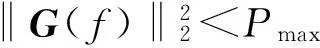
(5)

式中，‖·‖2表示向量的2范数，Pmax为扬声器能承受的最大功率。利用拉格朗日方法，式(5)可转化为不带约束的形式[10]：

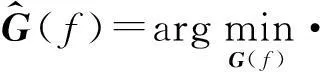
(6)

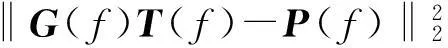
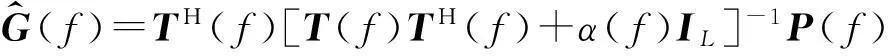
(7)

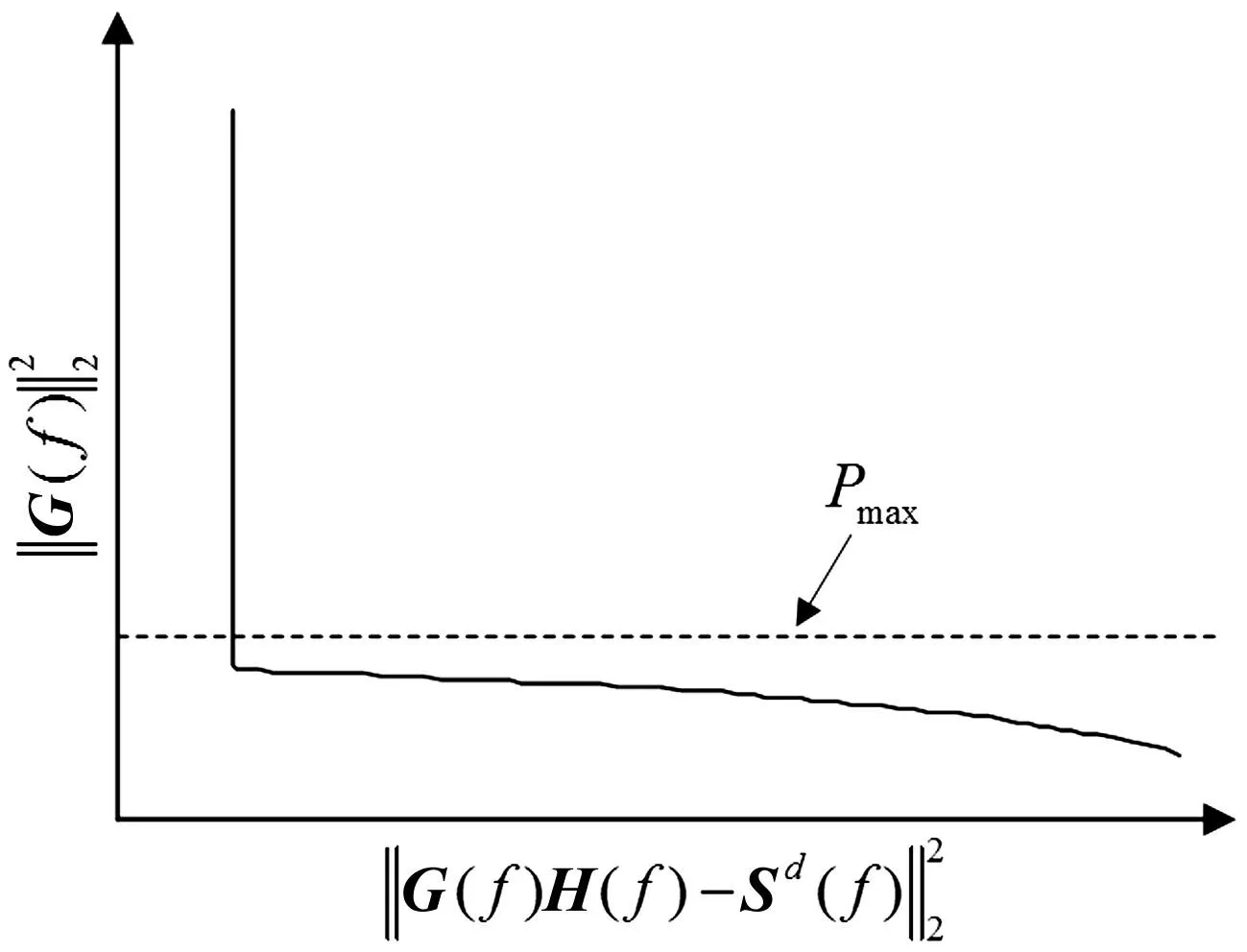
图3　L曲线法选择正则化参数 Fig.3 Regular parameter chosed by L-curve method

H(f)=TH(f)·

[T(f)TH(f)+α(f)IL-1]

(8)

H(f)是M×L维的矩阵。利用以上方法求取滤波器的频域特性时，根据原始声场特性的不同分为两种情况：当声场随时间的变化不大时，可以当做稳态声场处理，仅需要进行一次频域特性的求解，之后根据该频域特性设计滤波器对整段信号进行滤波；当声场随时间变化剧烈时，需要对原始声信号进行分段处理，分别求取各段的频域特性，之后根据针对各段信号设计滤波器，已获得更好的重现效果。

2.2L曲线滤波器设计

针对扬声器驱动信号这种连续时域信号，以式(8)为基础设计相应的时域滤波器。考虑到当控制点的数量M多于扬声器的数量L时，根据式(8)设计的时域滤波器倾向于不稳定[8]，选择使M小于L已获得滤波器的稳定性。采用频率采样法进行FIR滤波器设计，令h(tk)为需要求取的L曲线滤波器，具有以下形式：

(9)

式中，tk为离散时间序列，tk=kΔt，k= -N,-N+1,…，N-1。Δt为采样时间间隔，由采样频率fs决定。N为正整数。下面以hml(tk)为例说明h(tk)的设计方法。假定声场重现的频率范围为f∈[fL,fH]，H(f)也在此范围内才有值。hml(tk)对应的频域响应为Hml(f)，首先对Hml(f)进行频率采样，得到Hml(fn)，其中fn=fL+(n-1)Δf，且n为正整数，Δf为频率采样间隔。Δf的选择决定了滤波器的时间长度，Δf的值应取得足够小，以避免设计的滤波器出现时域混叠现象。采样频率fs满足fs>2fH，利用式(10)构造函数B(fn)：

(10)

式中，fn为离散频率序列，fn=nΔf，其中Δf=fs/(2N)，n=0,1,…,2N-1。(·)*表示取共轭。对B(fn)进行离散傅里叶逆变换

b(tk)=IDFT[B(fn)]Δf

(11)

式中，IDFT[·]表示离散傅里叶逆变换。k=0,1,…,2N-1。k的值与n的值一一对应。调整离散序列b(tk)的顺序得到hml(tk)：

hml(tk)=

(12)

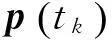
(13)

式中，τk和tj为离散时间序列。

3机械噪声重现实现验证

3.1实验方法

为了对L曲线滤波方法的有效性进行验证，选择实际汽车噪声作为目标进行重现。在声场中布置的控制点(M=18)如图4所示。控制点形成环形包络面，间距Δ≈0.1 m，因此该阵列可有效的重现1 700 Hz以下的声场。测量原始声场时直接将该阵列置于声场中进行测量，如图5。

图4 麦克风阵列Fig.4MicrophoneArray图5 实际噪声的测量Fig.5Measurementofpracticalnoise

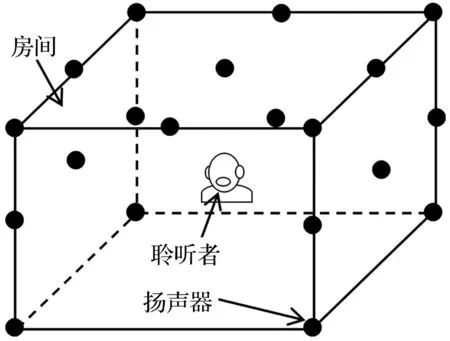
图6　扬声器阵列 Fig.6 Measurement of practical noise

进行声场重现时受到房间空间条件的限制，扬声器沿房间周边的布置(如图6)，共采用L=20个扬声器。

选择一辆乘用车以60 km/h匀速行驶时后排位置的噪声声场作为原始声场，该声场可以作为稳态声场处理。由于测量到的噪声信号主要在800 Hz以下，选择对fL=50 Hz到fH=800 Hz的声场进行重现。

3.2实验结果

图7　扬声器功率与重现误差的平衡 Fig.7 Balance of loudspeaker power and reproduction error

在求解L曲线滤波器的频域特性时，不同频率下绘制出的L曲线图。当频率为87 Hz时绘制出的L曲线如图 7所示。在本例中，Pmax的值选择为1W。从图中可以看出，在该频率下最优的正则化参数为L曲线上曲率最大点所对应的参数值。从后面的结果可以看出，L曲线法在控制扬声器功率的同时也保证了理想的重现精度。

在进行L曲线滤波器的时域设计时，当频率采样间隔Δf为1 Hz时，便可以避免时域混叠现象，此时的滤波器时间长度为1 s。滤波器设计完成后，利用(13)求得扬声器的驱动信号，其中第17个扬声器的驱动信号如图8所示。由于驱动能力的限制，扬声器驱动信号的幅值需要被限制在10 V以下。从图8可以看出，利用L曲线滤波方法得到的驱动信号幅值在5 V以下，可以满足系统驱动的要求。

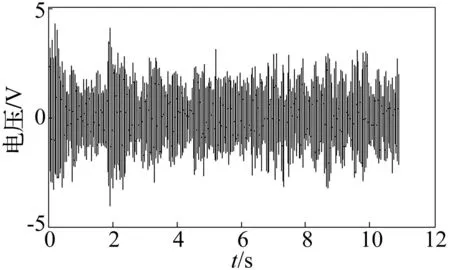
图8　实际扬声器激励信号g 17(t j) Fig.8 Loudspeaker signal in practice

原始声场和重现声场在第4个控制点处的声压级对比如图9(a)所示，从图中可以看出：在分析的有效时间内(11 s)，重现声场与原始声场的声压级接近。按照式(1)计算出的声场重现的误差如图9(b)所示，声场重现的时域声压级误差均值约为0.26 dB。

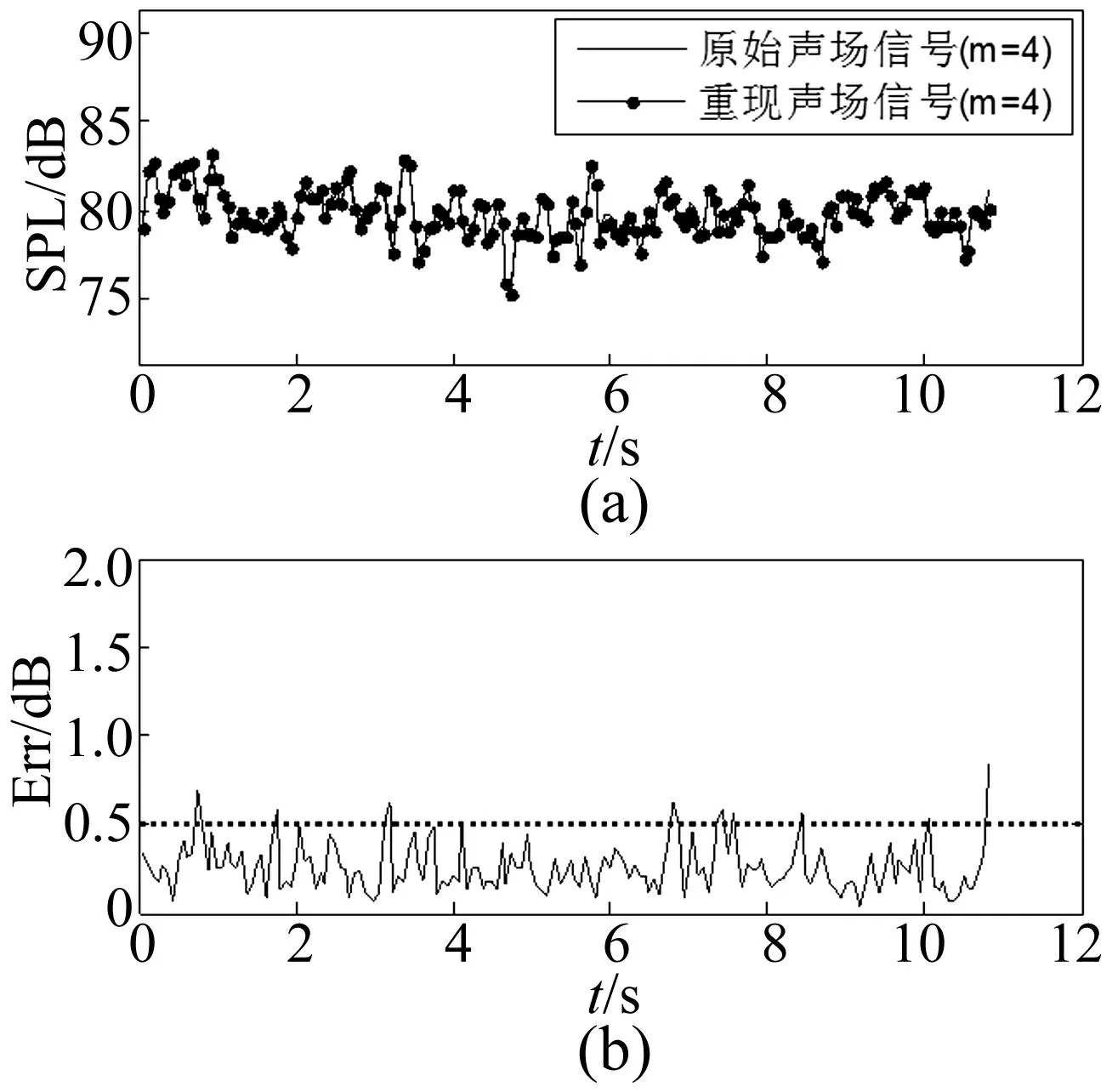
图9　时域声压级对比(a)和时域声压级误差(b) Fig.9 Sound pressure level comparason in time domain(a) and error(b)

取t∈(5 s,5.5 s)时间范围内原始声场和重现声场在第4个控制点处的数据进行幅值谱比较，结果如图10所示。可以看出：原始声场声压和重现声场声压的幅值曲线基本重合。

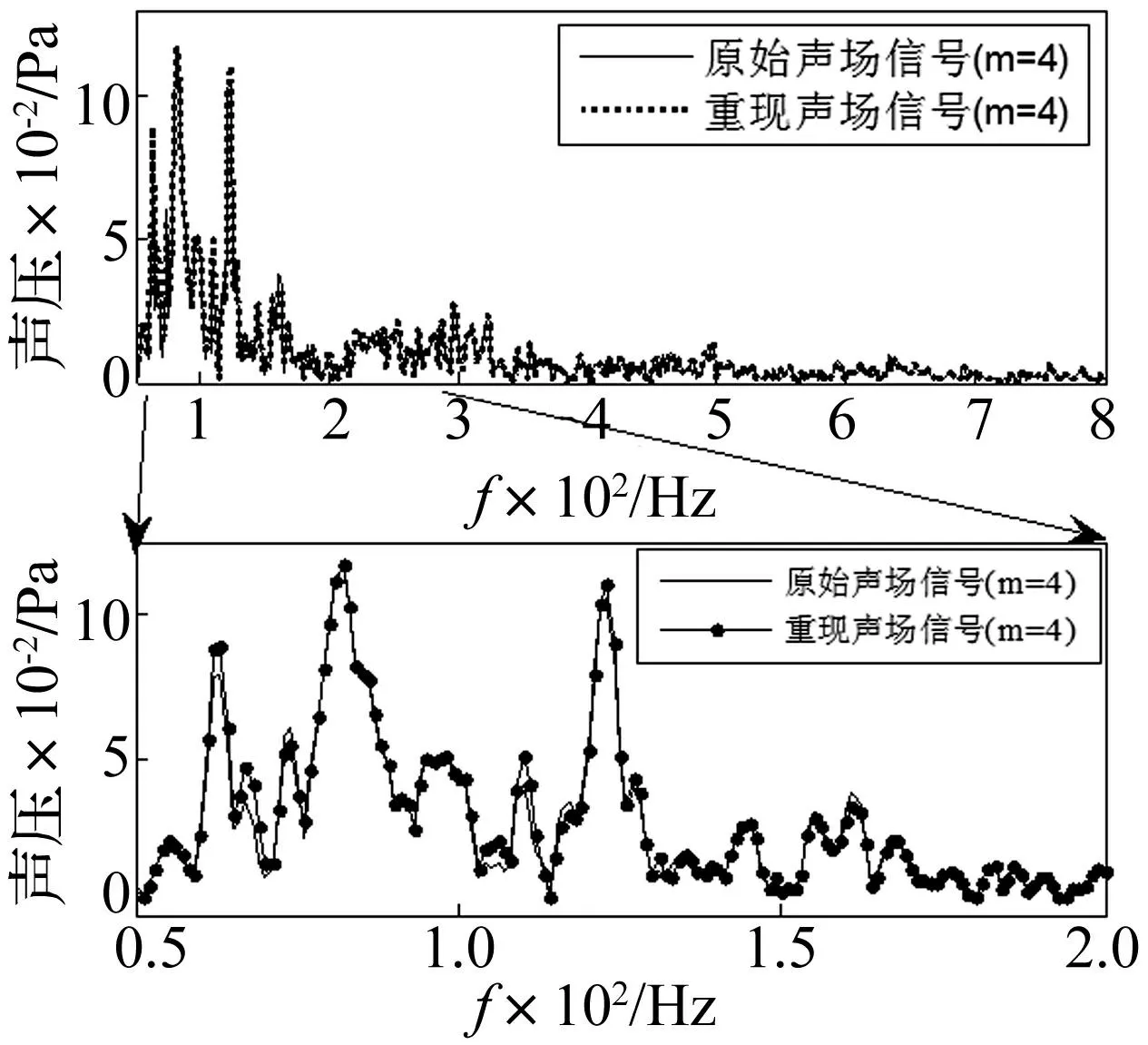
图10　频域幅值比较 Fig.10 Magnitude comparison in frequency domain

对比结果表明：L曲线滤波方法能够有效的获取实际扬声器的驱动信号，重现声场的各个频率成分的信息，在一般房间内实现稳态声场的定量重现。

4结论

论文建立了一般房间内用于声品质评价的声场重现的系统模型，并利用最小二乘法和L曲线法得到阵列扬声器驱动信号特性，然后进行阵列驱动信号的L曲线滤波器的设计，最后通过实际汽车噪声的重现对方法的有效性进行验证。结果表明：声场重现的L曲线滤波方法，实现了重现误差和扬声器驱动信号功率之间的平衡，克服了声场重现易产生的系统不稳定问题，可以在非自由场房间内实现稳态声场的定量重现。

参考文献

[1]Gerzon M A. Periphony: With-height sound reproduction[J]. Journal of the Audio Engineering Society, 1972,21(1):2-10.

[2]Daniel J, Moreau S, Nicol R. Further investigations of high-order ambisonics and wavefield synthesis for holophonic sound imaging[C]//Audio Engineering Society, 2003.

[3]Poletti M A. Three-dimensional surround sound systems based on spherical harmonics[J]. Journal of the audio engineering society, 2005,53(11):1004-1025.

[4]Betlehem T, Abhayapala T D. Theory and design of sound field reproduction in reverberant rooms[J]. The Journal of the Acoustical Society of America, 2005,117(4 Pt 1):2100-2111.

[5]Betlehem T, Poletti M A. Sound field reproduction around a scatterer in reverberation: Acoustics, Speech and Signal Processing[C]//IEEE International Conference on, 2009. IEEE.

[6]Trevino J, Okamoto T, Iwaya Y, et al. High order Ambisonic decoding method for irregular loudspeaker arrays[C]//Proceedings of 20th International Congress on Acoustics, Sydney:ICA,2010.

[7]Miyoshi M, Kaneda Y. Inverse filtering of room acoustics[J]. Acoustics Speech and Signal Processing, IEEE Transactions on, 1988,36(2):145-152.

[8]Nelson P A. Active control of acoustic fields and the reproduction of sound[J]. Journal of Sound and Vibration, 1994,177(4):447-477.

[9]KirkebyO, Nelson P A, Hamada H, et al. Fast deconvolution of multichannel systems using regularization[J]. Speech and Audio Processing, IEEE Transactions on, 1998,6(2):189-194.

[10]Choi H G, Thite A N, Thompson D J. Comparison of methods for parameter selection in Tikhonov regularization with application to inverse force determination[J]. Journal of Sound and Vibration, 2007,304(3):894-917.

[11]Betlehem T, Withers C. Sound field reproduction with energy constraint on loudspeaker weights[J]. Audio, Speech, and Language Processing, IEEE Transactions on, 2012,20(8):2388-2392.

[12]Hansen P C. The L-curve and its use in the numerical treatment of inverse problems[D]. IMM, Department of Mathematical Modelling, Technical Universityof Denmark, 1999.

第一作者潘雄男，博士，讲师，1977年生