某型号导弹发射过程中颤动现象的分析

某型号导弹发射过程中颤动现象的分析

商霖,王亮，金晶

(中国运载火箭技术研究院，北京100076)

摘要：某型号导弹发射过程中出现了振动突然放大的颤动现象。通过对振动信号的时域波形分析和频域谱分析，确认导弹局部振动的突然放大是一种自激振动现象。随后，采用相平面法通过对振动加速度信号进行频域积分得到发射过程中导弹局部的运动轨迹，并根据极限环理论证明了存在颤动现象。最后，论述了导弹局部的颤动现象是由于导弹与发射箱导轨之间的摩擦力所做正功大于负功而引起的，并通过涂抹较厚的润滑剂或润滑油消除了这种颤动现象。

关键词：发射动力学；颤动现象；信号分析；相平面法；极限环

中图分类号:V19文献标志码：A

基金项目：国家自然科学资金资助项目(51275262)

收稿日期：2014-04-18修改稿收到日期：2014-07-30

Chattering analysis for a missile during its launching

SHANGLin,WANGLiang,JINJing(China Academy of Launch Vehicle Technology, Beijing 100076, China)

Abstract:Chattering of a missile happens during its launching. Through analyzing signals in time domain and frequency domain, it was shown that the misile’s chattering is a self-excited vibration. The local motion trajectories of the missile during its launching were obtained through integrating its vibration acceleration in frequency domain with the phase plane method. Using the limit-cycle throry, it was proved that there is the chattering of the missile. Finally, it was found that the chattering of the missile is caused by the friction between the missile and the launch box’s track, it can be eliminated through daubing thicker lubricants on the track.

Key words:launching dynamics; chattering; signal analysis; phase plane; limit-cycle

某陆基型号导弹武器系统采用箱式倾斜热发射方式，主要由发射车、发射箱和导弹等部分组成。地面发射试验时发现，导弹在出箱过程中其局部在某一时段内发生了颤动，即弹体的自激振动现象。自激振动是工程领域中常见的一类周期性振动，尤其在机械加工、机构传动等领域。Altintas等[1-3]基于再生理论和实验模态分析，提出了几种模型用于预测分析在车削，铣削和钻孔操作中可能出现的自激振动现象。Luciano等[4]基于实验结果与理论分析的一致性验证，提出了一种R/S尺度分析方法用以监测和预测机械加工中可能出现的自激振动现象。Petrov等[5-11]从数学分析解常微分方程的角度出发对工程中遇到的自激振动现象进行了分析和研究。

当前，尚无导弹武器系统在发射过程中出现自激振动的报道和研究。本文从信号分析处理试验数据的角度出发对导弹发射过程中出现的颤动现象进行了分析。首先，通过对振动信号的时域波形分析和频域谱分析，确认导弹局部振动的突然放大是一种自振现象。随后，采用相平面法通过对振动信号进行频域积分得到发射过程中导弹局部的运动轨迹，并根据极限环理论证明了存在颤动现象。最后，论述了导弹发射过程中颤动现象的形成原因，给出了消除颤动现象的具体措施，并在后续发射试验中验证了这一措施的有效性。

1信号分析

1.1试验概述

试验前，在导弹各舱段内、前滑块和后滑块等位置各布置一个振动测点。采用有线测量方法，将振动信号通过低噪声电缆接入MDR数字信号记录器。其中，振动测量设备采用9101-J型传感器，频响范围5～8 000Hz。记录设备由一台32通道ICP电压型MDR组成，采样频率20480 Hz。在导弹振动工程[12]中，主要关心2 000 Hz以内的振动信号。由此，最高分析频率小于传感器固有频率的1/4，保证了测试信号的相频特性误差近似为0，相位畸变很小。同时，采样频率是最高分析频率的10.24倍，满足了采样定理[13]的要求。

试验时，利用起竖油缸将弹箱组合体起竖到规定发射角，利用回转油缸将弹箱组合体回转到规定方向角，导弹通过前、后滑块套接在发射箱导轨上。发射时，控制系统发出点火指令后，发动机正常点火、通过喷管排出高温、高压的燃气并推动导弹在导轨面上运动，前、后滑块按设计要求飞离导轨。试验过程中，利用导弹局部安装的振动传感器，获取了导弹发射过程中的加速度响应信号。

试验后，将各振动测点获取的加速度信号从记录设备中导出，并转换为物理量参数。考虑到振动测试过程中，存在着各种干扰信号，使得测试系统采集到的数据会偏离其真实数值，因此信号分析前对测试信号进行了去中心化、去趋势项和平滑降噪等预先处理[12]，同时采用经验模态分解方法[14]消除了测试信号中的高斯白噪声。限于篇幅，本文仅选取前滑块位置振动测点获取的加速度响应信号a(t)进行相关的信号分析。

1.2波形分析

图1为导弹局部的振动加速度时程曲线和加速度的瞬态均方根值时程曲线，分别对应于图中标识ACEL和RMS。从图1可见，①在t0～t1时段内，导弹敏感到的振动信号不大，且均方根值较为平缓；②t1->t2->t3->t4组成了一个梯形的振动波形图，其中在t1～t2和t3～t4的两个时段内，振动信号分别快速增加和快速减小；③在t2～t3时段内，导弹敏感到较大量级的振动信号，均方根值增大了约4倍。根据自激振动的特征[15]，在振动过程中，存在能量的输入和耗散，当输入的能量大于耗散的能量时，振动的振幅必增加；当输入的能量等于耗散的能量时，振动的振幅保持不变；当输入的能量小于耗散的能量时，振动的振幅必减小。这一特征描述与图1振动信号的梯状波形图的变化相吻合，表明导弹发射过程中发生了自激振动。

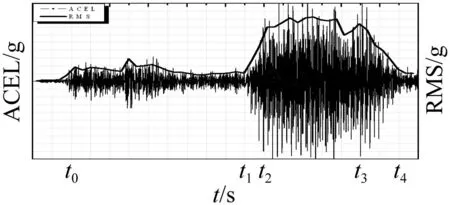
图1　振动信号的加速度和加速度均方根值时程曲线 Fig.1 The time history curve of vibration acceleration and its root mean square

1.3频谱分析

图2为导弹局部振动信号在t1～t4时段内的加速度功率谱密度曲线，图中标识为PSD。图3为导弹局部振动信号在t1～t4时段内的时频分析图，图中清晰而详细地显示了能量随时间和频率的二维分布，能量越高标涂颜色越深。由图2和图3可见，①功率谱密度曲线表现为随机性分量与周期性分量的叠加，周期性分量占主导，激励范围在中频段；②周期性分量集中在f1、f2、f3、f4和f5等频点(均出现较大谱峰)，这些频点与导弹固有频率成倍数关系；③时频分析图直观地表明了振动能量主要集中在f1、f2、f3、f4和f5等周期性频点附近(见图3中深色条形区域)，这些频点伴随了导弹局部振动放大的全时程。根据自激振动的定义[16]，其是一种恒频恒幅的周期性振动。自激振动的频率和振幅都由系统的物理参数确定，与初始条件无关，且产生自激振动的系统是非线性系统。由此，说明导弹发射过程中其局部振动的突然放大是自激振动。

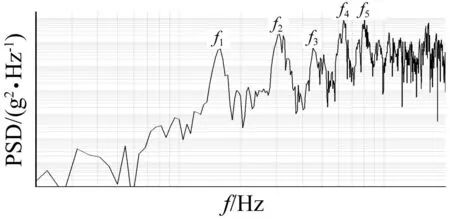
图2　振动信号的加速度功率谱密度曲线 Fig.2 Acceleration power spectrum density curve of vibration signal

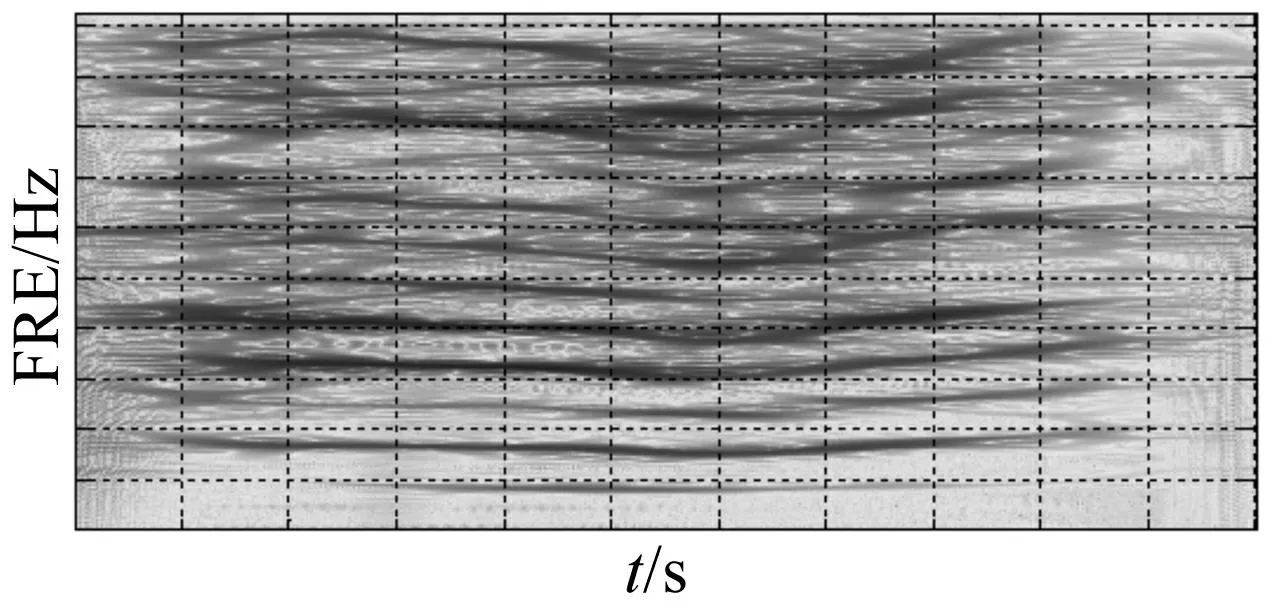
图3　振动信号的时频分析图 Fig.3 Time-frequency analysis figure of vibration signal

2颤动分析

颤动是摩擦力激励机械系统弹性模态产生的自振现象[16]。地面发射过程中，导弹局部的振动放大是一种颤动现象。此时，有多个弹性模态被激发(见图2和图3)。本文通过对加速度信号a(t)在[f1-df,f1+df]、[f2-df,f2+df]、[f3-df,f3+df]、[f4-df,f4+df]和[f5-df,f5+df]等5个频带上进行通带滤波，其中df为半带宽，从信号上将5个自由度的系统处理为5个单自由度的系统。由于5个单自由度系统的相轨迹基本一致，下文仅选取其一采用相平面法进行颤动分析。

2.1相平面法

2.1.1相平面

单自由度振动系统的自由运动方程可以简化为二阶自治方程

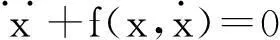
(1)

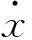
若令变量

(2)

则可将上述二阶方程变为两个一阶方程

(3)

上述二维变量(x,y)称为状态变量，方程(3)称为状态方程。以x和y为坐标轴构成的二维状态空间(状态平面)称为相平面，该平面上的点表示系统的特定运动状态，称为相点。

2.1.2相轨迹

给定运动起始时刻t=t0的状态变量x0和y0，构成系统的初始状态P0(x0,y0)，由状态方程(3)支配的运动过程，是从P0出发的曲线，称为方程(3)的相轨迹。

将方程(3)的两个方程相除，得到定义相轨迹曲线族的一阶微分方程

(4)

对式(4)进行积分，可得到包含任意积分常数的代数方程，对应着由不同初始相点P0出发的相轨迹族。

2.2极限环

自激振动的相轨迹应为相平面内孤立的封闭曲线，微分方程几何理论称它为极限环[16]。考虑到真实的动力学系统要承受外界扰动，不稳定的周期运动不能保持。因此，自激振动的相轨迹必须是稳定的极限环。

本文通过对振动加速度a(t)的一次积分和二次积分，得到了导弹局部的振动速度v(t)和振动位移l(t)，由此二维变量(l,v)就构成了导弹局部的相轨迹。信号积分操作通常有两种方法：时域积分和频域积分。一般认为[17]，频域积分要比时域积分效果更好，其原因是由于时域积分时积分一次就要去趋势，去趋势就会降低信号的能量，由此得到的结果会比真实幅值要小，所以本文选用频域积分法获取相轨迹。

图4为导弹局部的封闭相轨迹(即极限环)。由图4可见，导弹局部的相轨迹包含着两个极限环：一个对应于振动时段t0～t1，见图5(a)；另一个对应于振动时段t1～t4，见图5(b)。图5(a)中，相平面的环形区域在内、外边界上的相轨迹均指向环域外，而且环域内没有汇集相轨迹的奇点，表明这是一个不稳定极限环，系统不发生自激。图5(b)中，相平面的环形区域在内、外边界上的相轨迹均指向环域内，且环域内没有奇点(相轨迹的源)，表明这是一个稳定极限环，系统发生了自激。至此，证明了导弹发射过程中其局部出现了颤动现象。

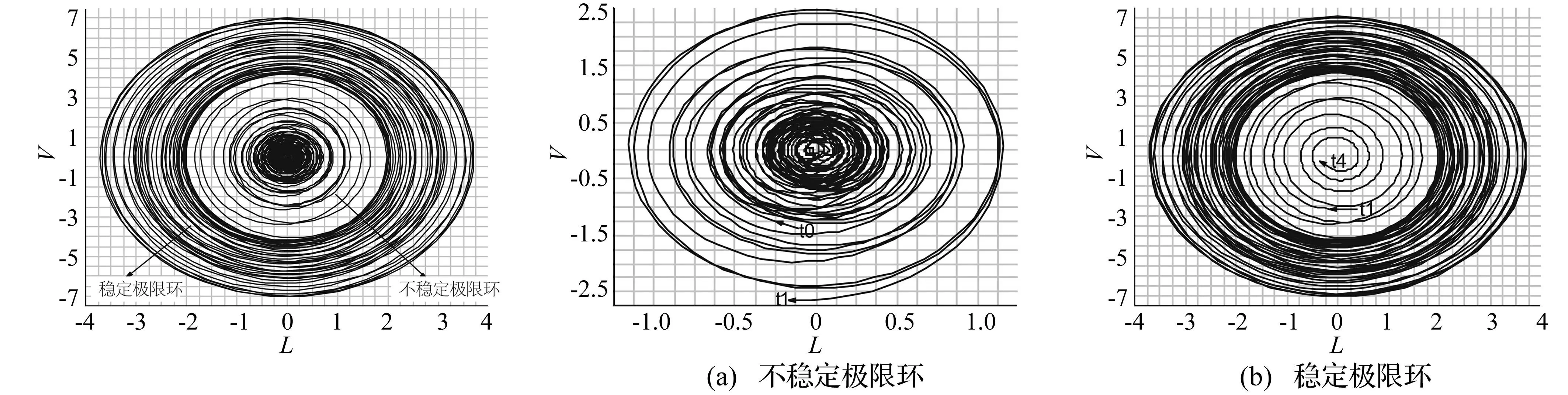
图4 导弹局部出现的极限环Fig.4Thelimit-cycle图5 稳定极限环与不稳定极限环的对比Fig.5Comparisonbetweenthestabilitylimit-cycleandtheunstablelimit-cycle

2.3颤动成因

物理学家哈尔克维奇曾经给自振系统定义[16]，他认为自振系统是主振体、能源、控制器和反馈单元组成的闭环系统，功能框图表示为图6。按照哈尔克维奇的定义，在导弹和发射箱组成的自振系统中，弹体和箱体构成主振体，发动机是能源，导弹的运动状态是控制器，导弹和发射箱导轨之间的摩擦力是反馈单元。

图6　形成自振的反馈机制框图 Fig.6 Feedback mechanism diagram of forming the self-excited vibration

在地面发射过程中，首先导弹依靠发动机推力运动起来，根据导弹运动状态弹轨之间提供摩擦阻力，当在一个振动周期内摩擦阻力对弹体所做的正功(负阻尼做功)大于负功(正阻尼做功)，使弹体振动的能量越来越大，即产生自激振动。因弹体的固有频率较高，故自激振动的振幅会迅速增大。由于弹箱组合体系统有阻尼存在，当在一个振动周期内由弹轨之间摩擦阻力提供的能量与系统阻尼消耗的能量平衡时，自激振动振幅趋于稳定(见图1)。

综上分析，导弹发射过程中的颤动现象是由于导弹与发射箱导轨之间的摩擦力作用而产生的。

3消除颤动的措施

要消除和预防导弹发射过程中出现的颤动现象，就要补偿弹轨间摩擦力中的负阻尼分量，有效的方案是施加足够的正阻尼力，抵消摩擦力中的负阻尼力的影响分量。这方面主要的措施是在导弹与导轨之间涂抹较厚的润滑剂或润滑油，由此变干摩擦为湿摩擦，变自激振动为粘性阻尼振动。采取这一措施后，某陆基型号导弹武器系统在后续多次地面发射试验中，导弹在出箱段其局部再未出现颤动的现象。

4结论

某型号导弹武器系统在地面发射过程中出现了颤动现象，产生了高频、高幅值的动态响应。本文通过对振动信号的时域波形分析和频域谱分析，确认导弹局部振动的突然放大是一种自振现象。同时，通过对振动信号进行频域积分得到导弹局部的运动轨迹，并根据极限环理论证明导弹局部存在自激振动。随后，从能量机理方面阐明了导弹局部的颤动现象是由于导弹与发射箱导轨之间的摩擦力所做正功大于负功而引起的。最后，通过涂抹较厚的润滑剂或润滑油消除了导弹发射过程中出现的颤动现象。

参考文献

[1]Altintas Y. Manufacturing automation, metal cutting mechanics, machine tool vibrations, and CNC design [M]. New York: Cambridge University Press, 2000.

[2]Budak E, Altintas Y. Analytical prediction of chatter stability in milling-part I: generalformulation [J]. Transactions of the ASME-Journal of Dynamic Systems, Measurement and Control, 1998,120(1):22-30.

[3]Budak E, Altintas Y. Analytical prediction of chatter stability in milling-part II: application of the general formulation to common milling systems [J]. Transactions of the ASME-Journal of Dynamic Systems, Measurement and Control, 1998,120(1):31-36.

[5]Petrov E P. Recent advances in numerical analysis of non-linear vibrations of complex structures with friction contact interfaces[J]. Progress in Industrial Mathematics ant ECMI 2006, 2008,12(11):220-224.

[6]张振果,张志谊,王剑,等．螺旋桨推进轴系摩擦自激扭转振动研究[J]．振动与冲击,2013,32(19)：153-158.

ZHANG Zhen-guo, ZHANG Zhi-yi, WANG Jian, et al. Friction induced self-excited vibration in a propeller shaft system [J]. Journal of Vibration and Shock, 2013,32(19):153-158.

[7]贾尚帅,丁千．刹车系统的摩擦自激振动和控制[J].工程力学,2012,29(3):252-256.

JIA Shang-shuai, DING Qian. Friction-induced self-excited vibration and control of a brake system[J]. Engineering Mechanics, 2012,29(3);252-256.

[8]郭桂祯,张雅卓,练继建.平面闸门垂向自激振动机理和稳定性研究[J].振动与冲击,2012,31(9):98-100.

GUO Gui-zhen, ZHANG Ya-zhuo, LIAN Ji-jian. Mechanism and stability of self-induced vertical vibration of plane gates[J]. Journal of Vibration and Shock, 2012,31(9): 98-100.

[9]李连进,罗鹏. 连轧管机的自激振动分析[J].湖南科技大学学报:自然科学版,2008,23(4):28-30.

LI Lian-jin, LUO Peng. Analysis of self-excited vibration of seamless tube rolling mills[J]. Journal ofHunan University of Science & Technology:Natural Science Edition, 2008,23(4):28-30.

[10]鲁晓燕,叶黔元,瞿志豪.一类轧机自激振动现象的分析与解决[J].上海理工大学学报,2004,26(2):39-43

LU Xiao-yan, YE Qian-yuan, QU Zhi-hao. Analysis and solution of the self-excited vibrationon a rolling mill[J]. J. University of Shanghai for Science and Technology, 2004,26(2):39-43.

[11]贾启芬,于雯,刘习军,等.多自由度分段光滑非线性系统的近似解——中华文物龙洗的自激振动[J].力学学报,2004,36(3):373-378.

JIA Qi-fen, YU Wen, LIU Xi-jun, et al. Appoximate analytical solution of the piecewise-smooth nonlinear systems of multi-degrees-of -freedom[J]. Acta Mechanica Sinica, 2004,36(3):373-378.

[12]黄怀德主编.振动工程[M].北京：中国宇航出版社,2005

[13]凌福根译. 随机数据分析方法[M].北京：国防工业出版社,1976

[14]郭喜平,王立东.经验模态分解(EMD)新算法及应用[J].噪声与振动控制,2008,28(5):70-72.

GUO Xi-ping, WANG Li-dong. New Aalgorithm of Empirical Mode Decomposition (EMD) and its application[J].Noise and Vibration Control, 2008,28(5):70-72.

[15]刘延柱,陈立群,陈文良.振动力学[M].北京：高等教育出版社,2011.

[16]丁文镜.工程中的自激振动[M].吉林：吉林教育出版社,1988.

[17]王济,胡晓.MATLAB在振动信号处理中的应用[M].北京：水利水电出版社,2006.

第一作者彭博男，博士，1989年11月生

通信作者郑四发男，副研究员，1970年10月生