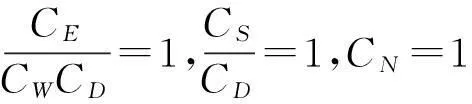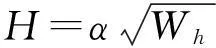基于加速度的强夯加固效果实时检测

基于加速度的强夯加固效果实时检测

夏东超，李万莉

(同济大学机械与能源工程学院，上海201804)

摘要：强夯法因其经济易行、效果显著、适用范围广等优点在地基处理工程中得到了日益广泛的应用。目前强夯施工时一般依据强夯技术规程采用测量夯沉量的方法来实时检测夯实程度，但现有的测量夯沉量的方法存在诸多弊端，为改变此现状，提出了利用强夯冲击时夯锤的加速度来实时检测强夯夯实程度的方法。首先建立强夯碰撞模型，通过理论分析推导出夯锤加速度与夯击次数的关系，然后依据相似原理搭建试验模型，进行模型试验得出数据验证，最后得出单击夯沉量和峰值加速度的相对变化百分比之间的相互关系，并提出以基于加速度的强夯效果实时检测设想，为施工中强夯加固效果实时检测提供新思路。

关键词：强夯；加速度；实时检测

中图分类号:TU662文献标志码：A

收稿日期：2014-04-18修改稿收到日期：2014-07-16

Dynamic compaction real-time detection based on acceleration measurement

XIADong-chao,LIWan-li(School of Mechanical Engineering, Tongji University, Shanghai 201804, China)

Abstract:With advantages of easy use, low cost, good effects and wide application range, the dynamic compaction is widely used in ground construction. According to its technical regulations, the ramming value measurement methods are currently applied in the real-time compaction level detection, but the existing methods all have their defects. To improve the situation, using the rammer impact acceleration to detect the compaction level. Firstly, the dynamic compaction’s impact model was established and the relationship between the rammer’s acceleration and ramming times was derived through theoretical analysis, then the test model was built based on the similarity theory, the model tests were conducted to get data for verification. The final results showed that the relation between relative change percentages of a single ramming value and peak acceleration is obtained, the assumption detecting real-time compaction level based on impact acceleration is deduced, thus a new way to detect the real-time compaction during the construction is provided.

Key words:dynamic compaction; acceleration; real-time detection

强夯法又称动力固结法，即用起重设备反复将夯锤起吊到一定高度，然后利用自动脱钩释放载荷或带锤自由落下的方式，使夯锤的动能在土中形成强大的冲击波和高应力，从而提高地基的强度、降低压缩性、改善其抵抗振(震)动液化能力、消除湿陷性等的一种方法。该法自1969年诞生以来以其经济易行、效果显著、设备简单、施工方便、材料节省、质量易控、适用范围广、施工周期短等突出的优点，在世界各地多种类型、多种目的的地基处理工程中得到了日益广泛的应用[1]。在我国，随着“十二五”规划的全面展开，国内大规模城镇化建设、工程基础设施建设的持续，地基处理工程越来越普遍，强夯法必将得到更加广泛的应用。

强夯质量检测是指通过对影响强夯地基加固效果的因素进行实时动态测定来确定强夯地基加固的质量及其变化趋势，目的是保证强夯法施工能够实现设计要求的处理效果。对于强夯施工质量的实时监测，一般采用测量夯沉量的方法,主要分为三类：传统人工测量夯沉量；利用编码器或者特制码盘测量卷扬出绳量再通过计算相对差值求得夯沉量；利用超声波或者激光测距等非接触方式测量锤顶到标称位置的距离来计算夯沉量。目前，强夯施工过程质量监控使用最为普遍的方法是利用人工水准仪进行夯沉量观测，但该法效率低、精度差且存在较大的安全隐患；利用编发器或者特制码盘测量卷扬绳出绳量的方法不仅需要在卷盘上增加机械结构和开始信号传感器，而且可能由于地面较为松软或振动导致强夯机下陷，影响测量高度，带来误差，同时如若发生钢丝绳在卷筒里乱绳也会影响测量结果；利用超声波或者激光测距等非接触方式测量则会因为强夯施工环境恶劣，在强振动、高温、大雾、灰尘量大等因素下不能准备测量。针对上述问题，本文根据强夯冲击力与地基土体密切相关的物理事实，提出了利用测量夯锤冲击加速度(即冲击力)来实时监测强夯质量的设想，展开了基于冲击加速度的强夯质量实时监测方法的研究，从理论模型和实验两方面进行说明验证。

1强夯加固过程的动力分析

1.1强夯法的加固机理

对于强夯法的加固机理，虽然存在很多不相统一的观点，但目前比较普遍的观点认为：在强大的夯击能下地基中产生强烈的冲击波和动应力，导致土中孔隙减少，孔压上升，土体局部出现液化，在夯击点周围产生裂隙，形成树枝状的良好排水通道，使得孔隙水顺利逸出，于是土体迅速固结，以达到减少沉降，提高承载力的目的。经过强夯后，土体强度提高过程可分为夯击能量转化、土体液化或土体结构破坏、排水固结压密、触变恢复并伴随固结压实四个阶段[2]，其中第一阶段是瞬时发生的，第四阶段是强夯终止后很长时间才能达到的，一般可长达几个月以上，第二和第三阶段则介于上述二者之间。

1.2非完全弹性碰撞强夯模型

图1　强夯作用简化模型 Fig.1 Simplifieddynamic compaction model

强夯过程是一极其复杂的力学行为，涉及到土力学、水力学、碰撞理论、弹塑性力学、水动力学、土动力学、波动力学等理论。在现阶段，要想通过复杂深奥的理论推演以求达到精确的描述几乎是不可能的，而且容易脱离实际。因此，本文的机理研究基于现实的物理过程，使用考虑夯锤与土体共同作用的非完全弹性碰撞半空间强夯模型[3]，如图1所示进行简化，将强夯过程分解为两个过程：非完全弹性碰撞与弹簧阻尼一维振动。当自由下落的夯锤夯击土体时，在接触的瞬间，夯锤的速度由下落结束的初速度v11减小到一个新的接触后初速度v12。这时夯锤与土体已经接触，所以v12也是紧贴夯锤底面处受压缩土体的初始速度。另外，伴随冲击，土体的局部范围将产生非常高的应力，波速在土体中扩散开去。其结果为：阶梯型的应力波以相应的地震波速传播到所有质体的内部。这些应力波将保持动量守恒，并且进一步将这种突如其来的局部速度的变化传播到土介质中去。

质量为m1的物体和质量为m2的两物体发生碰撞，两物体的运动轨迹在同一条直线上。m1和m2两物体在接触前质心的速度分别为v11和v21；碰撞接触后速度分别为v11和v21。由动量守恒定律可得：

m1v11+m2v21=m1v12+m2v22

(1)

其速度变化关系式为

(2)

式中:Rc为恢复系数。

Rc=1时为完全弹性碰撞，物体在碰撞结束后，变形恢复完全，动能没有发生损失；Rc=0时为完全非弹性碰撞或塑性碰撞，即在碰撞结束后，物体的变形量丝毫没有得到恢复；0

联立(1)和(2)式解得：

(3)

(4)

土体的碰撞恢复系数Rc和参振土体的质量m2是影响夯锤速度v12变化的两个最主要因素。碰撞恢复系数Rc介于0到1之间，并且和土的类型、含水量和密实度等因素相关。参振土体m2和土的性质、夯锤底面面积和底面形状等都有关系。从现场观测可假定参振土体m2是和夯锤同底面，高度按土的类型、含水量和密实度等因素而在0倍～1倍的夯锤高度范围内变化的圆柱体的质量，它是反映夯锤和土体相互作用关系的重要因素之一。在一般情况下，土体的密实度越大，重度越大，碰撞恢复系数也越大；参振土体的体积越小，形变过程的初速度v12则越大，反之亦然。当Rc=0～0.5时，v12/v11≈0.83；当Rc>0.5时，v12/v11将随Rc的增大也快速增大[4-5]，如图2所示。

图2　恢复系数和v 12/v 11的关系 Fig.2 Relationship between coefficient of restitution and v 12/v 11

1.3动力平衡方程的建立求解与冲击加速度分析

上述的非完全弹性碰撞半空间强夯模型，其半空间和其表面及其上的质量块所共同组成的体系，具有无限多个自由度，从自由振动的角度来说，它应该具有无限多个“振型”。Gutzwiller[6]用数学的方法严密地表达了这种瞬态混合边界值的问题，然后再用正交多项式的方法进行求解。所得解说明，除去极复杂和极短的初始阶段，这种瞬态振动可近似用一个最基本的“振型”来描述，这就从理论上分析了用等效集总的单自由度模型来模拟这个问题的可能性。因此，本文将地基简化成阻尼一弹簧体系，Cz为地基竖向阻尼系数，kz为地基竖向弹簧系数，其值分别为[7-8]：

式中，r0为夯锤的半径；G、ρ、μ分别为半空间的剪切模量、密度和泊松比。

(5)

式(5)中第一项为夯锤与地面接触碰撞后所具有的冲击力，第二和第三项分别是地基对夯锤的运动阻力和变形阻力，而这两种阻力都与夯锤的运动方向相反。将上式整理后得：

(6)

(7)

对于欠阻尼系统，上式的通解为：

(8)

(9)

(10)

(11)

式中，ωn为无阻尼圆频率，fd为有阻尼时的圆频率；β为阻尼比。

根据式(4)令：

(12)

(13)

E为弹性模量，由此可解得：

(14)

至此，方程求解完毕。

由式(9)可推算得夯锤的加速度时程关系为：

(15)

通过式(15)可知，冲击加速度不仅考虑了夯锤的相关参数，如锤重、底面积和落距，还考虑了地基土体的物理性质，如弹性模量、密实度和泊松比，最后还考虑了夯锤和土体之间的相互作用，如参振土体和恢复系数。

考虑到目前仍没能提出一个适合同填土地基分析使用的土体弹性模量随夯击次数变化的规律，加固区内土体弹性模量随夯击次数变化的规律就沿用了钱家欢等[5]提出的经验公式：

EN=E0×N0.516

(16)

式中，EN为夯击N次后加固区内土体的弹性模量；E0为原始弹性模量；N为夯击次数。

土体密度的改变一般表现于表层土体，而较深层土体的密度一般没有发生改变，所以可以认为不影响地基竖向阻尼系数Cz。将式(16)代入式(15)可求得每一击的加速度峰值，其汇总如图3所示，可知从冲击加速度峰值总体来看，其随夯击次数的增加呈现逐渐增大的趋势，但该趋势逐渐放缓，最后趋近于某一定值。

图3　冲击加速度汇总 Fig.3 All data of impact acceleration

2模型实验装置搭建

由于强夯法施工的特殊性导致现场原尺度试验的经济成本太高，本文利用室内模型进行模拟实验来推导夯锤加速度和加固效果之间的关系。根据相似定理[9]，采用量纲分析法，施工参数考虑夯击能E、夯锤质量W、夯击次数N、夯锤底面直径D、夯击高度h、干重度ρd和夯沉量S，用函数形式表示为：f(E,W,S,N,h,D,ρd)=0，取W和D为基本量纲，根据π定理对其余四个物理量进行量纲分析，得到无量纲群：

再根据相似理论，由上式可得到各相似指标：

本文所模拟的夯锤实际底面直径为2.36 m，锤重为20 t，本试验所设计的模型夯锤锤重50 kg，底面直径0.32 m，如图4，并据此可得：

实验所用土体取自附近在建体育场施工工地土体，测得其物理力学性质如表1所示，土体松散不均匀，为粉质粘土，有砂感，低含水量土体。

表1　土体物理力学性质

图4　夯锤整体结构 Fig.4 Rammer model

图5　模型实验箱 Fig.5 Test box model

图6　加速度数据采集硬件系统 Fig.6 Acceleration data collection system

图7　夯锤悬停在设定高度 Fig.7 Hammer hovering on the set height

实验时，加速度传感器安装于夯锤内部，使用行车起吊夯锤到设定高度，图7为夯锤悬停在设定高度的状态，待夯锤平稳后，启动安装于桁架上的电葫芦用于使脱钩器旋转以释放夯锤，图8为脱钩后夯锤夯击实验土体后状态，至此完成一次夯击实验，重新起吊夯锤至指定高度后，进行再次夯击，循环上述操作至设定夯击次数。

图8　夯锤夯击土体 Fig.8 Hammer compacted to the soil

3加速度实验数据分析

本文模拟500 kN·m和750 kN·m这两种施工常用的小级别强夯能级，选择下落高度分别为0.5 m和0.75 m，土体选择和现场一致，收锤标准根据《建筑地基处理技术规范》要求按比例缩放：当单击夯击能小于4 000 kN·m时最后两击夯沉量平均值不宜大于50 mm，根据CS=7.375，可求得模型试验时当最后两击夯沉量平均值不超过6.8 mm时，夯击结束。

图9为10击夯击的加速度数据的汇总。峰值加速度指每一击冲击加速度的峰值；单击夯沉量指每一击夯击结束后较其上一击的沉降量；累计夯沉量指每一击夯击结束后较未夯时的沉降量。由图可以得到：峰值加速度随着夯击次数的增加同时也逐渐增加，最后逐渐趋向于某一值；单击夯沉量着夯击次数的增加也逐渐增加，最后稳定于一定范围内；累计夯沉量则随着着夯击次数的增加逐渐增加。第五击到第十击的夯沉量分别为8 mm、6 mm、3 mm、4 mm、2 mm、3 mm，所以按照最后两击夯沉量平均值不超过6.8 mm，认为在第七击时夯击结束。

图9 50cm下落高度的夯沉量和峰值加速度Fig.9Rammingvalueandpeakaccelerationofheight50cm图10 50cm下落高度的峰值加速度和相对变化百分比Fig.10Peakaccelerationandrelativechangepercentageofheight50cm图11 50cm下落高度的单击夯沉量和相对变化百分比Fig.11Singlerammingvalueandrelativechangepercentageofheight50cm

图12 75cm下落高度的夯沉量和峰值加速度Fig.12Rammingvalueandpeakaccelerationofheight75cm图13 75cm下落高度的峰值加速度和相对变化百分比Fig.13Peakaccelerationandrelativechangepercentageofheight75cm图14 75cm下落高度的峰值加速度和相对变化百分比Fig.14Singlerammingvalueandrelativechangepercentageofheight75cm

图10和图11分别为50cm下落高度的峰值加速度和相对变化百分比和50 cm下落高度的单击夯沉量和相对变化百分比，可以看出，单击夯沉量和峰值加速度的相对变化百分比的变化呈现相同的趋势，都随着夯击次数的增加逐渐减小，最后趋近于某一值。第六击和第七击的单击夯沉量的平均值小于6.8 mm时，夯击结束，它们的峰值加速度相对变化百分比都小于5.4%，最后两击的平均峰值加速度的相对变化百分比为4.85%。所以在50 cm的下落高度情况中，当最后两击的平均峰值加速度的相对变化百分比小于4.85%时，夯击应结束。

图12为75 cm下落高度的夯沉量和峰值加速度，可以得到：峰值加速度随着夯击次数的增加同时也逐渐增加，最后逐渐趋向于某一值；单击夯沉量着夯击次数的增加也逐渐增加，最后稳定于一定范围内；累计夯沉量则随着着夯击次数的增加逐渐增加。第五击到第七击的夯沉量分别为10 mm、6 mm、4 mm，所以按照最后两击夯沉量平均值不超过6.8 mm，认为在第七击时夯击结束。

同样，从图13和图14中可以得出，75 cm下落高度的单击夯沉量和峰值加速度的相对变化百分比的变化呈现相同的趋势，都随着夯击次数的增加逐渐减小，最后趋近于某一值。第六击和第七击的单击夯沉量的平均值为5 mm小于6.8 mm，夯击结束，它们的峰值加速度的相对变化百分比都小于5.8%，平均值为5.1%。所以，在75 cm的下落高度情况中，当最后两击的平均峰值加速度的相对变化百分比小于5.1%时，夯击应结束。

根据上述50 cm下落高度和75 cm下落高度的数据分析，本文认为单击夯沉量和峰值加速度的相对变化百分比存在一定的对应关系，当夯沉量达到停夯要求时，峰值加速度的相对变化百分比也相应的已小于某一值。因此，在强夯作业时，可以通过测量峰值加速度计算相对变化百分比来判断强夯是否应该结束，实时判断是否需要停夯。

4结论

强夯法因其经济易行、适用范围广等优点在地基处理工程中得到了广泛的应用。但强夯加固机理极为复杂。本文采用非完全弹性碰撞半空间强夯模型对其进行简化，从理论上分析了强夯夯击次数与加速度相互的关系，分析了单击夯沉量和峰值加速度的相对变化百分比之间的相互关系。并提出以基于加速度的强夯效果实时检测设想，为实际应用于强夯施工提供了较为重要的参考。

参考文献

[1]刘春,翁洋,王汉强.波动理论在强夯加固机理研究中的应用[J].土工基础,2004, 18(1):47-49.

LIU Chun , WEN Yang , WANG Han-qiang. The application of wave theory in the mechanism of subgrade reinforcement by dynamic compaction[J].Soie Engineering and Foundation,2004,18(1):47-49.

[2]孙永平,膝凯,张玉环.强夯法施工锤重参数的合理选用[J].勘察科学技术,1999,2:38-40.

SUN Yong-ping, XI Kai, ZHANG Yu-huan. The reasonable choice of tension weight parameter for dynamic consolidation construction [J].Technology of Communications, 1999,2:38-40.

[3]水伟厚.冲击应力与10 000 kN·m高能级强夯系列实验研究 [D].上海：同济大学，2004.

[4]钱家欢, 帅方生.边界元法在地基强夯加固中的应用[J]. 中国科学A辑, 1987,3:329-336.

QIAN Jia-huan, SHUAI Fang-sheng. The boundary element method in the application of the foundation consolidation [J].Science in China Series A,1987,3:329-336.

[5]钱家欢, 钱学德, 赵维炳, 等. 动力固结的理论与实践[J]. 岩土工程学报, 1986,8(6): 1-17.

QIAN Jia-huan, QIAN Xue-de, ZHAO Wei-bing. Dynamic consolidation theory and practice [J]. Chinese Journal of Geotechnical Engineering, 1986,8(6): 1-17.

[6]Gutzwiller M C. The impact of a rigid circular cylinder on an elastic solid[J]. Philosophical Transactions of Royal Society of London Series A:Mathematical and Physical Sciences, 1962,255(1053):153-191.

[7]孙进忠, 谭捍华, 祁生文, 等. 强夯振动的频域分析[J]. 岩土工程学报, 2000, 22(4): 412-415.

SUN Jin-zhong, TAN Han-hua, QI Sheng-wen. Frequency domain analysis of dynamic compaction vibration[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(4): 412-415.

[8]蔡袁强,陈仁伟,徐长节.强夯大变形加固机理的数值分析[J].浙江大学学报,2005,39(1):65-69.

CAI Yuan-qiang, CHEN Ren-wei, XU Chang-jie. Numerical analysis of dynamic compaction using large deformation theory[J]. Journal of Zhejiang University, 2005,39(1):65-69.

[9]赵康,石亮，罗嗣海.一种便携强夯模型实验装置的设计及应用[J].西安建筑科技大学学报,2012,44(2):224-230.

ZHAO Kang, SHI Liang, LUO Si-hai. The design of convenient device for dynamic compaction model test and its application [J]. Journal of Xi’an University of Architecture & Technology, 2013, 44(2):224-230.

第一作者商霖男，高级工程师，1977年生