基于单脉冲测角理论的相位中心计算方法∗

(电子科技大学电子工程学院,四川成都611731)

0 引言

相位中心计算是后续信号处理的前提和基础。在GPS系统中,地面接收天线相位中心的确认是GPS系统精确定位的前提[1-2];在抛物面天线中,只有将其馈源相位中心置于抛物面焦点附近,才能够得到较高的抛物面天线增益以及较低的副瓣[3]。在相控阵系统中,相位中心计算问题也具有十分重要的意义。对于单脉冲测角而言,子阵相位中心的精确程度对测角结果具有很大的影响;多相心天线和相心偏置天线以其相位中心的准确位置为系统接收和发射信号的基点[4];干涉合成孔径雷达相位中心的准确标记是其能够清晰成像的前提和重要保障。

因此,相位中心的计算受到广泛关注。目前的方法主要有模拟退火算法[5-6]、相位梯度算法和最小二乘算法。对于相位梯度算法,必须知道主瓣上各点的精确相位梯度值,并用拟合的方法来计算,得到的梯度值往往都是近似值,用近似的梯度值再进行近似的拟合,误差的累积较大,导致计算结果偏差较大[7-8]。而基于求偏导式矩阵元素的最小二乘法也会由于误差累积,引入较大偏差,得到不够准确的结果[9-10]。并且上述两种算法更多关注天线相位方向图的信息,而不关心天线本身的形状和结构等,它们都是通过分析主瓣方向图来标记天线的相位中心。

在实际的相控阵天线工程应用中,一般都将天线阵列进行子阵划分,使得天线具有子阵对称等结构特点,比如铺路爪雷达和丹麦眼镜蛇雷达[11]等。基于这个特点,本文从信号处理的角度出发,结合单脉冲测角的相关理论,提出一种新的求解相位中心的计算方法。

1 问题模型

在很多雷达中,通常对天线阵列进行子阵划分并且使子阵间具有一定的对称特性,如空警-2000、铺路爪雷达、丹麦眼镜蛇雷达等。这样不仅可以使理论分析得到简化,而且可以获得更优的性能。

大型相控阵雷达的天线布阵通常采用密度加权方式实现。密度加权的特点是对于有源阵元来说,它们之间的间距是不相等的。一般采用对有源阵元和无源阵元的规则排列来实现,具体来说,阵列几何中心周围有源阵元数多,越远离阵列中心有源阵元数越少,无源阵元数越多,同时还要满足越靠近天线阵列中心的阵元间距越小[12-13]。

以美国的铺路爪雷达为例,其密度加权的布阵方法如下:首先对圆面阵进行矩形栅格化的密度加权,天线单元分为有源阵元和无源阵元。设矩形栅格的单元数为N×N,单元间距为d,圆面阵直径上放置阵元的最大数为J,定义圆阵面的中心在[(N+1)/2,(N+1)/2],半径r=(N+1)/2,则阵元(m,n)距阵面中心的距离为

则矩阵栅格形成圆面阵的加权系数为

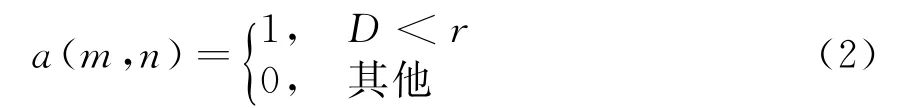
设距离天线中心为D的阵元对应的归一化参考电流分布值为I mn,该参考电流分布值在0到1之间产生。将有源阵元是否放置在该天线栅格的概率定为I mn。设一个在(0,1)之间服从均匀分布的随机数为X,若X＞I mn,则有源阵元不放置在该天线栅格上,可将无源阵元放置该位置;若X≤I mn,则有源阵元放置在该天线栅格上。常用的参考电流分布函数主要有圆孔径分布、泰勒圆口径分布、贝里斯圆口径分布[14]。这里用圆孔径分布,其函数值I mn与阵元到中心的距离、圆阵面半径、加权系数有关,具体表达式如下:

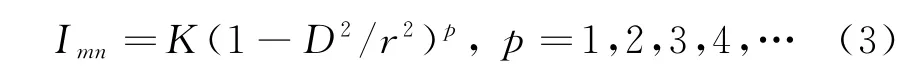
式中,D为加权阵元距离阵面中心的距离,r为圆阵面的半径,p为圆孔径加权函数的阶数,K为有源单元出现概率的比例因子。

图1为铺路爪雷达阵列天线的仿真图。

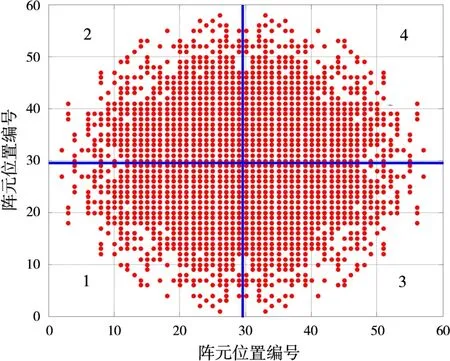
图1 铺路爪雷达阵元分布图

铺路爪雷达通过把圆面阵划分成4个子阵来测角,各子阵阵元具有相互对称性。由于子阵的对称性,该面阵天线的相位中心就在该分布图的几何中心(29.5,29.5)处,但是由于子阵的阵元具有不规则分布特点,因此很难确定该子阵的相位中心。在单脉冲测角等计算模型中,至关重要的一步就是获取该子阵的相位中心。本文的相位中心计算方法是专门针对这种具有子阵对称特性的相控阵天线模型而言的,该方法基于相位和差测角理论,充分利用子阵对称特点,具有很高的准确度。

2 基于单脉冲测角的相位中心计算方法

针对上节所述的天线阵列模型,本文提出一种基于单脉冲测角的相位中心计算方法。该方法充分利用子阵间的对称特性,将子阵相位中心信息与天线和波束、俯仰差波束及方位差波束输出关联起来,通过和差波束相比反推出子阵相位中心的计算公式。

2.1 相位差计算

在相控阵雷达目标探测等应用场合,阵列通常垂直放置,阵面的法线方向指向水平方向,仍以X轴为参考,角度的定义有:

方位角φ,-90°～90°,信号入射方向在XOZ面投影与Z轴的夹角。

俯仰角θ,-90°～90°,信号入射方向与XOZ面投影的夹角。

以美国铺路爪雷达天线阵面为例,采用图2定义方式。

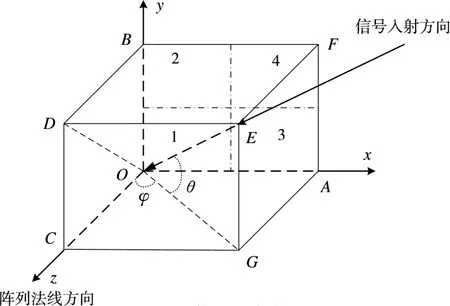
图2 信号入射模型

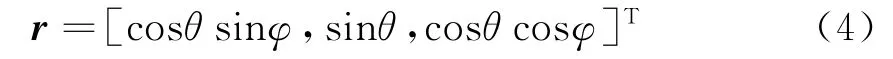
以该角度定义表示的信号方向向量为以第1子阵为参考,子阵2,3,4的坐标为

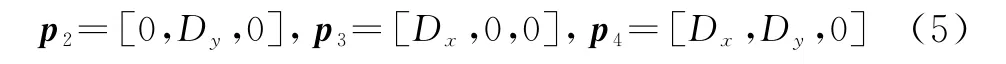
各子阵接收信号的相位差为

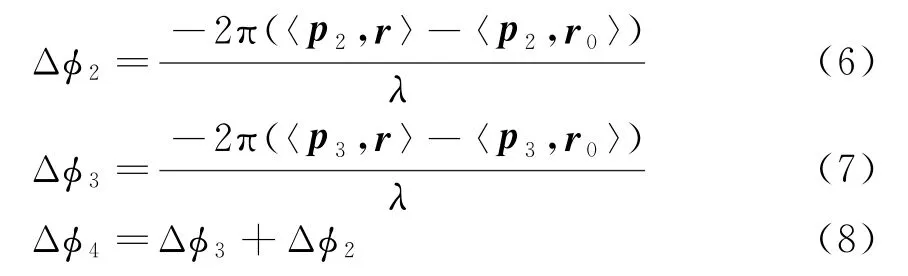
式中,r0为波束指向方向向量。

2.2 相位中心与和差波束的关系推导

设各子阵结构完全相同,第1子阵输出信号y1(n)=z1(n),为L个阵元的合成:

且Δγ=γ0-γ,γ0是阵元波束指向的控制相位,γ是来波的实际空间相位。

则其他3个子阵输出为

则和波束输出为

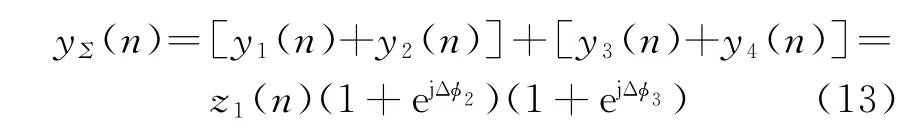
俯仰差波束输出为

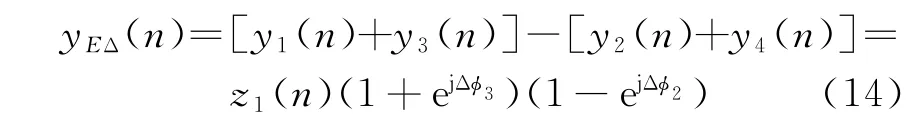
式(13)和式(14)联立求解可得第2个子阵接收信号的相位差:

由于波束指向角度为φ0,θ0,信号实际指向角可表示为

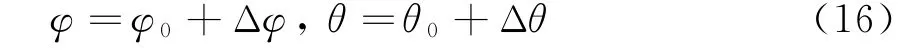
下面推导相位中心与和差波束、波束指向角以及信号来向角之间的关系式。

由于目标信号来向与波束指向角度相差很小,可以近一步化简:

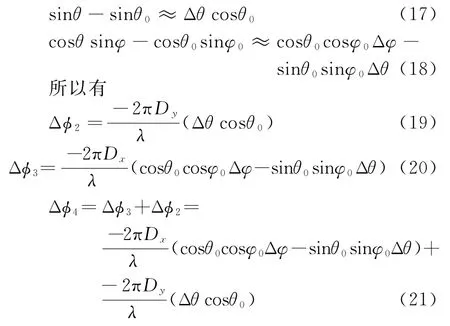
上述公式表明,D y与Δϕ2有直接关系,而Δϕ2与和差波束比值有直接关系,这样可以消除中间变量Δϕ2,得到D y与和差波束比值的关系式:

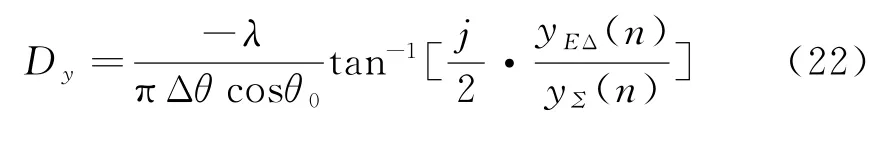
再推导D x与和差波束比值的关系,首先方位差波束输出为

进而得到波束比幅输出为

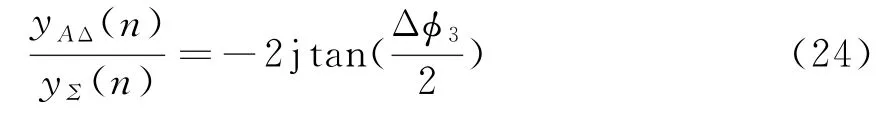
可以看到Δϕ3与波束比幅输出有直接关系:

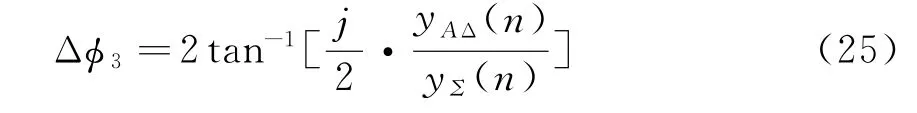
由于D x与Δϕ3有直接关系式,所以消去Δϕ3,可以建立D x与和差波束比值的间接关系式:

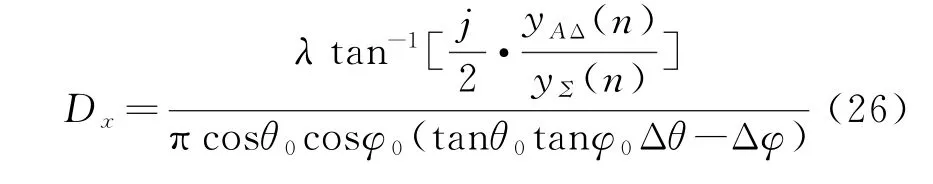
上式表明,D x和D y都与和差波束比值、波束指向角θ0,φ0以及目标信号来向角θ,φ有关。其中,和差波束比值可以由接收信号得到;于是,对于多组天线波束指向角及目标信号来向角,可以得到多组子阵相位中心。

相位中心的基本定义是:与天线相关的某点,若以该点为辐射远场球面的圆心,则辐射球面上给定分量的相位是一个常数,至少在辐射的关键区域满足[15-16]。换句话说,绝对意义上的相位中心点是不存在的,只能找到近似准确的视在相位中心。将这些相位点所在的位置区域看作视在相心区域,目标是找到该视在相心区域的中心,将其标记为该子阵的相位中心点。

2.3 基于和差波束的相位中心计算方法

计算相位中心点的具体步骤:首先给定波束指向角θ0和φ0,取一定范围内的目标信号来波方向角θ和φ,值得注意的是,目标信号来波方向角必须与波束指向角相差不大,否则会产生相位模糊问题;然后代入上述公式中求出一系列D x和D y;最后对求得的一系列D x和D y取平均值再除以2得到,作为子阵1的相位中心值。

3 仿真分析

下面以美国铺路爪雷达的相位中心计算为例。铺路爪雷达在满阵条件下,要求圆形口径,直径为22 m,阵元总个数为2 676个阵元。其相控阵天线的阵元位置分布采用密度加权方式产生,分4个子阵,如图1所示。接下来利用上述的公式计算该子阵1的相位中心点。

3.1 本文算法的仿真分析

1)波束指向(0°,0°),将信号来向俯仰角固定为0°,方位角扫面范围(0.1°～0.5°),根据式(26)计算的D x如图3所示。

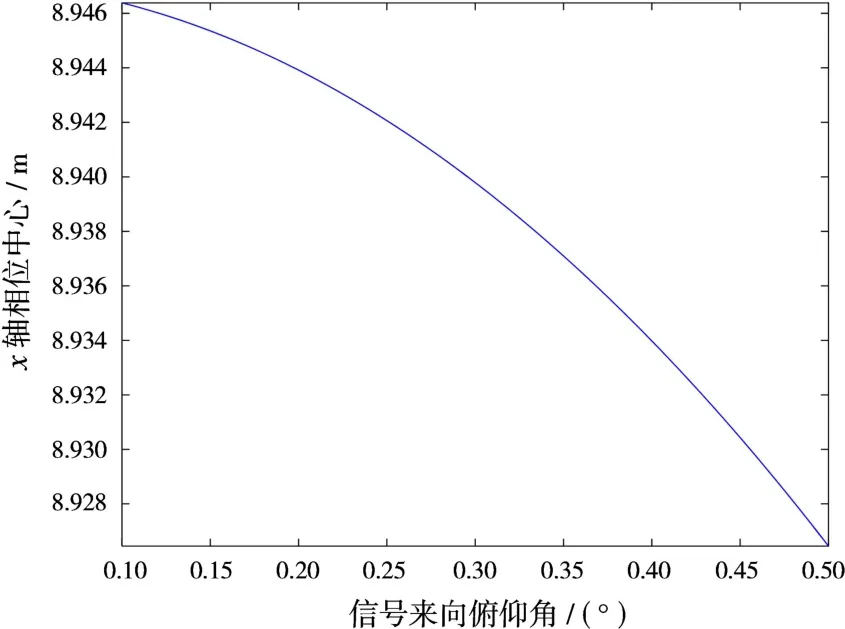
图3 在波束指向(0°,0°)下x轴相位中心变化曲线

由仿真结果可以看出,D x随信号来向角在小范围内变化,因此实际取平均可得到D x=8.935。

2)波束指向(0°,0°),信号来向方位角为0°,俯仰角扫面范围(0.1°～0.5°),根据式(26)计算得到的D y如图4所示。

图4 在波束指向(0°,0°)下y轴相位中心变化曲线

由仿真结果可以看出,D y随信号来向角在小范围内变化,因此实际取平均可得到D y=8.852。

3)波束指向(30°,30°),信号来向俯仰角为30°,方位角扫面范围(30.1°～30.5°),计算得到的D x如图5所示。

由仿真结果可以看出,D x随信号来向角在小范围内变化,因此实际取平均可得到D x=8.941。

图5 在波束指向(30°,30°)下x轴相位中心变化曲线

4)波束指向(30°,30°),信号来向方位角为30°,俯仰角扫面范围(30.1°～30.5°),计算得到的D y如图6所示。

图6 在波束指向(30°,30°)下y轴相位中心变化曲线

由仿真结果可以看出,D y随信号来向角在小范围内变化,因此实际取平均可得到D y=8.777。

经过不同角度下的试验可以得到相近的结果,在上面的基本概念部分提到绝对的相位中心点是不存在的,对于该圆形面阵而言,其相位中心集中在一块范围较小的位置区域中。一般在工程应用中,可以认为相位中心是恒定不变的,对于铺路爪雷达而言,其子阵1的相位中心近似有

3.2 性能的对比分析

下面与文献[9]中相位梯度算法进行对比仿真分析。仿真结果表明,本文所提算法具有更高的精确度。

目前文献中尚未见到能定量评价相位中心计算准确度的方法。我们注意到,在式(26)中,相位中心计算的准确性直接影响单脉冲测角结果。基于该原因,本文提出采用单脉冲测角精度来定量评价的相位中心计算精确度。基本思路为指定位于远处某角度的目标,用图1所示的相控阵天线对其进行单脉冲测角,相控阵天线的相位中心分别取本文所提算法计算值和相位梯度算法计算值,同时为了消除实验中随机量影响,采用2 000次蒙特卡洛实验得到测角结果统计图,根据统计结果定量评价两个算法的精确度。

仿真场景:相控阵天线如图1所示,目标距离雷达2 000 km,目标角度值为(30.2°,30.2°),天线波束指向为(30°,30°)。进行2 000次蒙特卡洛实验,可以得到单脉冲相位和差测角结果的统计图,如图7、图8所示。图7和图8中,横坐标表示单脉冲测角结果,纵坐标表示该测角结果出现的次数。

图7 本文方法的单脉冲测角结果统计图(方位向)

图8 本文方法的单脉冲测角结果统计图(俯仰向)

图7和图8表明,用本文方法所求得的相位中心值进行单脉冲测角,俯仰角和方位角的量测值都在30.2°附近,误差不会超过0.03°,测角精度较高。由于相位和差测角对子阵的相位中心准确度要求较高,因此这也反映了本文提出的相位中心计算方法有较高的准确性。

为了进一步体现该方法的优势,用相位梯度法来计算图1的子阵相位中心,得到D x≈D y=7.836。然后在相同的情况下用该值进行单脉冲相位和差测角,也进行2 000次蒙特卡洛实验。可以得到如图9和图10所示的统计结果。

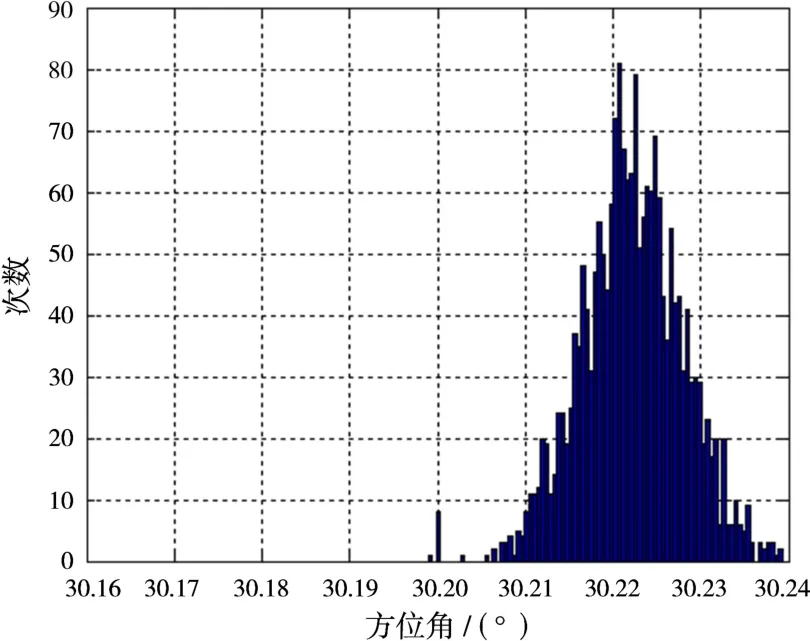
图9 文献[9]中相位梯度算法的目标方位角量测统计

图10 文献[9]中相位梯度算法的目标俯仰角量测统计

从上图中明显看出,测角结果偏差较大,目标信息来向角在30.2°,而实验结果大多分布在其右侧,左右误差范围跨度大于0.08°,甚至出现了一些孤立野值。对于远程预警雷达而言,角度偏差较大。实验结果直观地反映出相位梯度法计算出相位中心不够准确。通过两种方法的测角实验对比可以发现,利用本文提出的算法准确度更高、更可靠。

4 结束语

现有的相位中心计算方法大多从天线方向图及电磁波与电磁场角度去分析求解。而本文从相控阵信号处理的角度出发,提出一种新的相位中心计算方法。该方法首先计算出阵列天线的和波束函数、俯仰差波束函数、方位差波束函数;然后借鉴单脉冲测角理论,用和波束与俯仰差波束、方位差波束相比;最终反推出相位中心的表达式。与已有方法相比,本方法可以得到更高的准确度。

[1]董建明,魏亮,易卿武.卫星导航测量型天线的相位中心标定[J].无线电工程,2014,44(6):47-50.

[2]杨社年,王迎节.卫星导航接收天线相位中心的测量[J].无线电工程,2006,36(5):33-35.

[3]连培园,段宝岩,王伟,等.远场反推变形反射面天线馈源调整量[J].西安电子科技大学学报(自然科学版),2014,41(5):105-111.

[4]KONG R,YU Q L,SU D.Analysis for Phase Center of Pyramidal Horn Antennas for out of Band[C]∥9th International Symposium on Antennas Propagation and EM Theory,Guangzhou:IEEE,,2010:49-52.

[5]姜铁华,苏东林,杨争光.基于模拟退火算法的对数周期偶极天线相位中心计算[J].微波学报,2007,23 (增刊):35-38.

[6]JIANG T H,SU D L,YANG Z G,et al.Calculation for the Phase Center of LPDA Based on Simulated Annealing Algorithms and MOM[C]∥4th Asia-Pacific Conference on Environmental Electromagnetics, Dalian:IEEE,2006:670-673.

[7]THOVINEN J,LEHTO A,RAISANENN A.A Novel Differential Phase Method to Measure Phase Pattern and Phase Center of a Horn Antenna at 110 GHz [C]∥International Symposium of Antennas and Propagation Society,Dallas,Tx:IEEE,1990:1298-1301.

[8]TAGGART D,SACKS L.The Calculation of the Phase Center for Spacecraft Phased Array Antenna [C]∥Military Communications Conference,San Diego,CA:IEEE,1995:1046-1050.

[9]李锐,李建新.大型相控阵天线阵面相位中心定位技术研究[J].微波学报,2010,26(6):42-45.

[10]尚军平,傅德民,邓颖波.天线相位中心的精确测量方法研究[J].西安电子科技大学学报(自然科学版),2008,35(4):673-677.

[11]任晓飞,赵地,龚书喜,等.天线阵元相位中心的一种测量方法[J].舰船电子对抗,2014,37(2):103-106.

[12]MOHEB H,SEBAK A,SHAFAI L.Phase Centre Analysis of Array Antennas and Its Significance for Microwave Landing System[C]∥7th International Conference on Antenna and Propagation,York,UK: IEEE,1991:213-216.

[13]张根烜,查金水,胡劲松.大型相控阵雷达阵面结构设计研究[J].雷达科学与技术,2016,14(3):337-342. ZHANG Genxuan,ZHA Jinshui,HU Jinsong. Structural Design of Antenna Array of Large Phased Array Radar[J].Radar Science and Technology, 2016,14(3):337-342.(in Chinese)

[14]李世强,杨汝良.天线相位中心偏移方位多波束合成孔径雷达的误差分析[J].电子学报,2004,32(9): 1436-1440.

[15]潘超,张任,李瑞.阵元失效对相控阵天线低副瓣的影响分析[J].舰船电子工程,2016,36(4):83-85.

[16]DIONIGI M,MONGIARDO M,TOMASSONI C. Investigation on the Phase Center of Ultra Wideband Discone Antennas[C]∥German Microwave Conference,Berlin:IEEE,2010:59-62.