信道距离差异对统计MIMO雷达检测性能影响∗

费太勇,谭贤四,曲智国,邹立平,王 红

(1.空军预警学院,湖北武汉430019;

2.中国人民解放军93253部队,辽宁大连116019)

0 引言

多输入多输出(MIMO)雷达是利用多个发射天线同步地发射正交的波形,同时使用多个接收天线接收回波信号,并集中处理的一种新型雷达体制[1]。其中,统计MIMO雷达(以下简称MIMO雷达)具有良好的空间分集增益、结构增益和极化分集增益[2]。众多学者对MIMO雷达通过空间分集增益来提高雷达系统的检测性能进行了深入的研究[3-14]。然而这些研究包含了一个重要的前提条件,即MIMO雷达探测目标时信道间的距离(发射天线到目标再到接收天线的距离)近似相等。事实上,MIMO雷达探测目标时并不一定处处满足上述条件,尤其是当MIMO雷达波长较长时为获得空间分集增益MIMO雷达天线间的间距较远,此时MIMO雷达在探测某些位置的目标时信道间的距离差异较大而不能再认为近似相等。本文将对这种信道间的距离差异对MIMO雷达检测性能的影响进行研究。

1 MIMO雷达信号模型

假设MIMO雷达有M个发射天线和N个接收天线,其中第m个发射天线记为T m,第n个接收天线记为Rn,目标记为o′。根据双基地雷达方程[15], MIMO雷达接收天线R n与发射天线T m形成的信道nm接收到的目标回波复信号可表示为

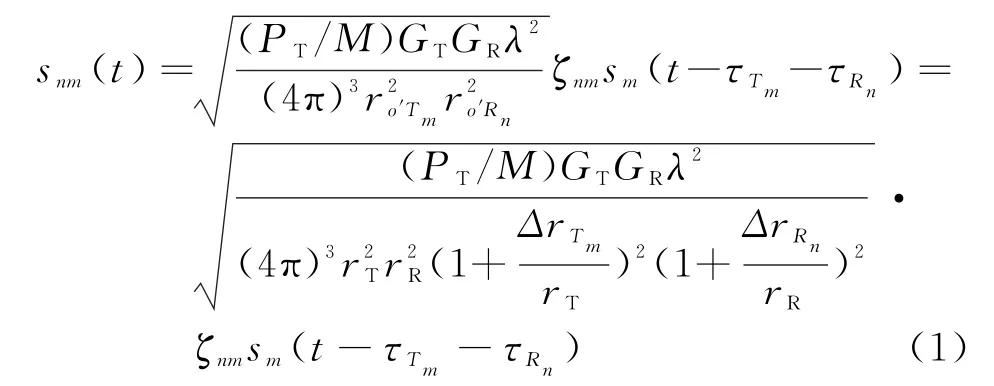
式中:PT为MIMO雷达总的发射脉冲功率;GTGR分别为发射天线和接收天线的增益;λ为信号波长;r o′Tm为o′到T m的距离,r o′Rn为o′到R n的距离;ζmn为目标在nm信道中的RCS所对应的电压散射系数[4],假设目标雷达截面积(Radar Cross-Section,RCS)为σ0且为Swerling 1型,则ζnm服从均值为0、方差为σ0的复高斯分布[16],假设MIMO雷达收发天线的位置满足文献[3]中空间分集的条件,则各信道的电压散射系数是独立同分布的;s m(t)为T m发射的信号,‖s m(t)‖2=1;τTm,τRn为o′到T m,R n的距离所对应的信号时延;rT,rR分别为o′到发射天线几何中心和接收天线几何中心的距离;Δr Tm=r o′Tm-rT,Δr Rn=r o′Rn-rR。

式(1)可进一步写成

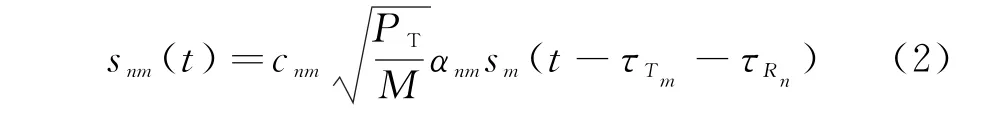
2 MIMO雷达的似然比检测

2.1 MIMO雷达信号处理流程

MIM O雷达信号处理流程如图1所示。接收天线R n接收的信号可表示为

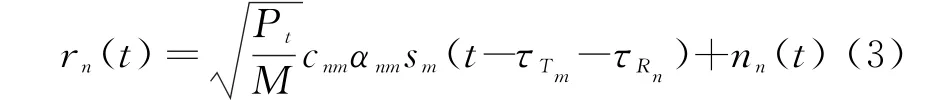
式中,n n(t)为高斯白噪声。由于发射信号的正交性,N个接收天线接收的信号通过匹配滤波器组,可将M个发射信号所对应的目标回波进行分离,从而得到N×M个不相关的目标回波,即对目标形成N×M个独立的观测通道。由于目标回波在每个通道的时延可能是不同的,所以需要对目标进行空间配准和包络对齐[7,17],然后再进行似然比检测。

图1 MIMO雷达信号处理流程图

2.2 MIMO雷达的似然比函数

当某检测单元存在目标时,nm信道在该检测单元的采样值可近似为

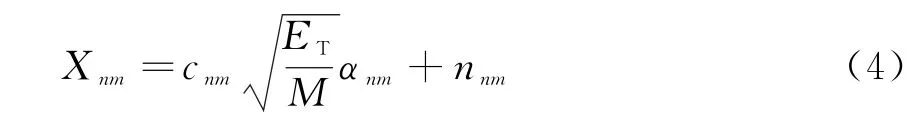
式中:ET=PTTs为MIMO雷达发射脉冲的能量;Ts为发射脉冲宽度;n nm为高斯噪声,方差为σn。故相应的信噪比可表示为

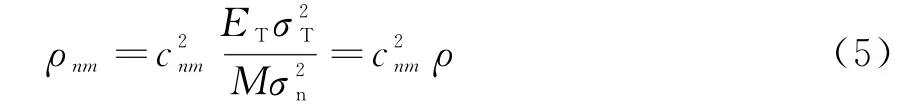
MIMO雷达的N×M个通道在目标检测单元的采样值的求模输出为

由于统计MIMO雷达各信道的电压散射系数是独立同分布的,故无信号(H0)和有信号(H1)时x的概率密度函数为

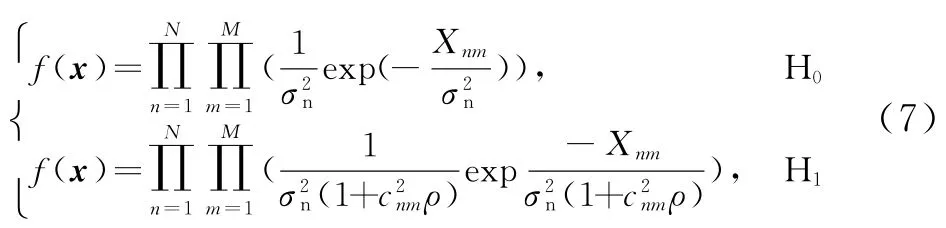
相应的似然比函数为

对式(8)两边取对数,得对数似然函数比为

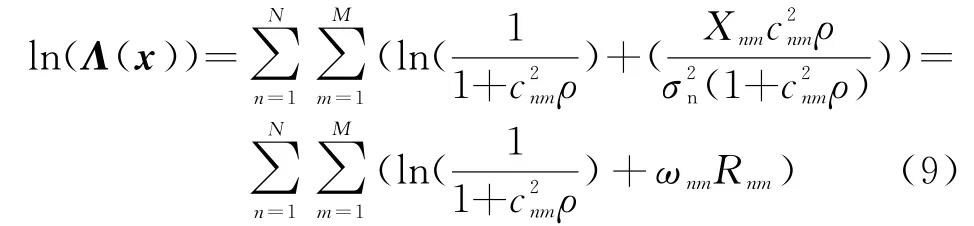
2.3 检验统计量的分布

当检测单元无信号时:

根据文献[18]的结论,独立同分布的指数分布随机变量的加权和近似服从伽马分布,即

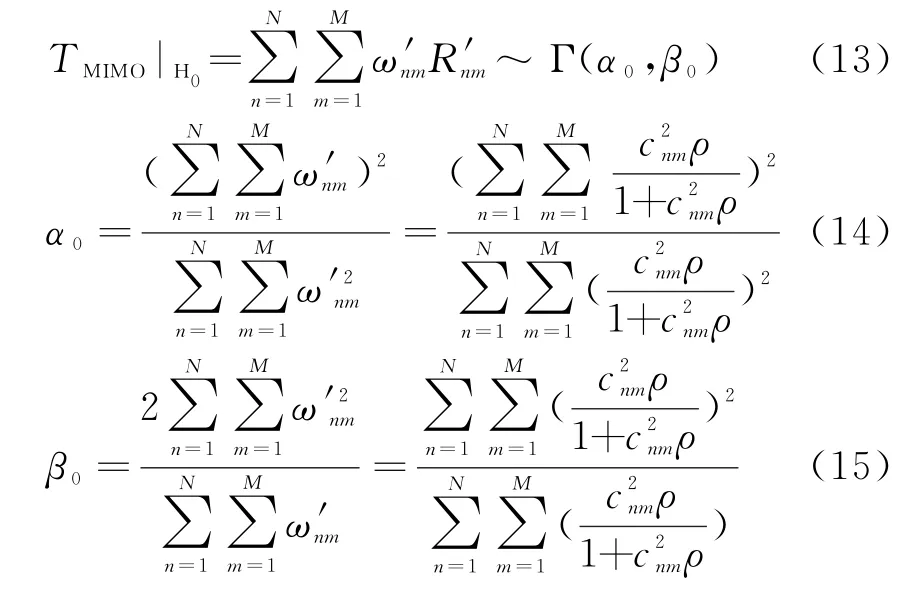
式中,伽马分布X～Γ(α,β)的概率密度函数为

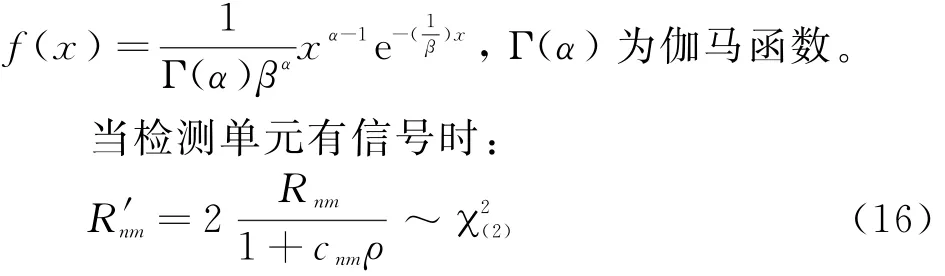
由式(10)、(13)、(17)得

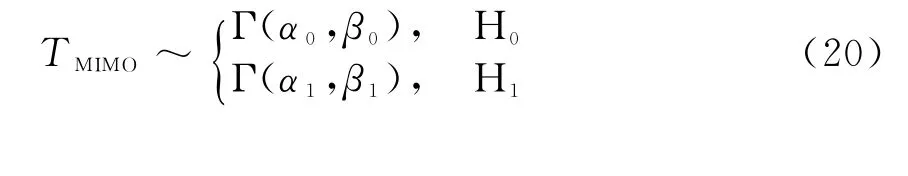
3 信道距离差异对检测性能的影响

式(2)、(5)表明信道间的距离差异会导致信道间目标回波信噪比的起伏,这种信噪比的起伏可用向量表示为

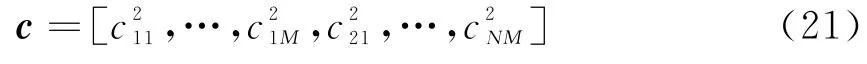
当MIMO雷达信道间无距离差异时,c为全1向量,此时无信噪比的起伏。距离差异越大,信噪比的起伏越大,为此定义信噪比的起伏度为

由式(20)的推导过程可知,检验统计量TMIMO中的参数α0,β0,α1,β1都是c的函数,在参考信噪比ρ一定的条件下,TMIMO的检测性能完全由c确定。为了定量研究c对TMIMO检测性能的影响,可采用文献[3,19]中的偏离系数d来对TMIMO的检测性能进行度量,即

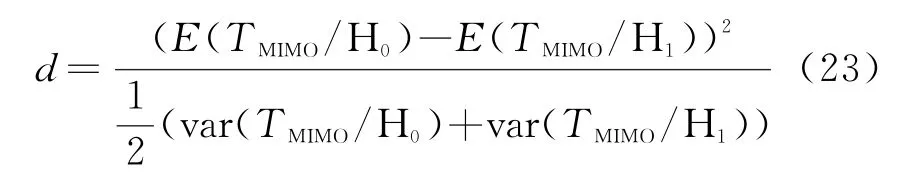
d越大表示检验统计量TMIMO越容易区分H0假设和H1假设,即检测性能越好。

因为伽马分布Γ(α,β)的均值为E(X)=αβ,方差为D(X)=αβ2,由式(13)～(15)和式(17)～(19),式(23)可变为

当c为全1向量,Δ=0,式(24)变为

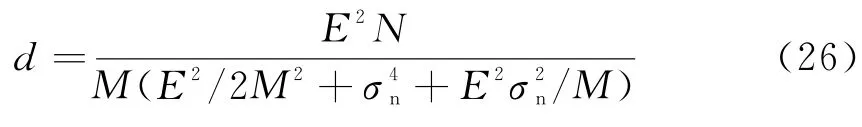
式(26)与文献[3]中的式(41)是一样的,这进一步验证了似然比函数及其统计特性推导的正确性。

4 仿真实例与数据分析

在xoy平面内,假设MIMO雷达的天线布置如图2所示,天线直角坐标分别为R1(-20 km,0),T1(-10 km,0),R2(0,0),T1(10 km,0),R3(20 km, 0),收发天线几何中心均为坐标原点o。假设目标以50 km的半径绕原点飞行,则目标的极坐标为o′(50 km,θ)。目标方位角θ与信噪比起伏度Δ的关系如图3所示。

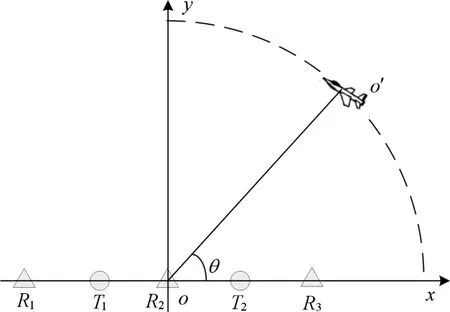
图2 MIMO雷达天线位置布置和目标探测示意图

图3 目标方位角与信噪比起伏度的关系

由于MIMO雷达天线是线性布置,当目标位于线阵的法线方向时,信道间的距离差异最小,此时信噪比起伏度最小;当目标偏离法线的角度越大,信道间的距离差异越大,此时信噪比的起伏度越大。

当参考信噪比分别为ρ=3,ρ=5,ρ=10时,信噪比起伏度与检验统计量TMIMO的偏离系数d的关系曲线如图4所示。从图4可以看出,随着信号起伏度的增加,偏离系数d都有不同程度的下降,即检测性能有不同程度的下降。但参考信杂比ρ不同偏离系数d下降的幅度是不同的。下面进一步考察偏离系数d与参考信噪比的关系。

图4 信噪比起伏度与偏离系数的关系

当目标方位角分别为θ=π/2,θ=5π/18,θ=π/9时,由图3可知其对应信噪比起伏度分别为Δ=0.08,Δ=0.42,Δ=0.84,此时偏离系数d随参考信杂比ρ的变化如图5所示。当参考信噪比(ρ＜2)较小时,信噪比起伏度对偏离系数d的影响不大,而且此时信噪比起伏度越大偏离系数d反而越大;但随着参考信噪比的增加,信噪比起伏度对偏离系数d的影响逐渐增大,例如当ρ=10 dB时,Δ=0.84较Δ=0时的偏离系数从d≈10下降到d≈6,下降幅度超过1/3。

5 结束语

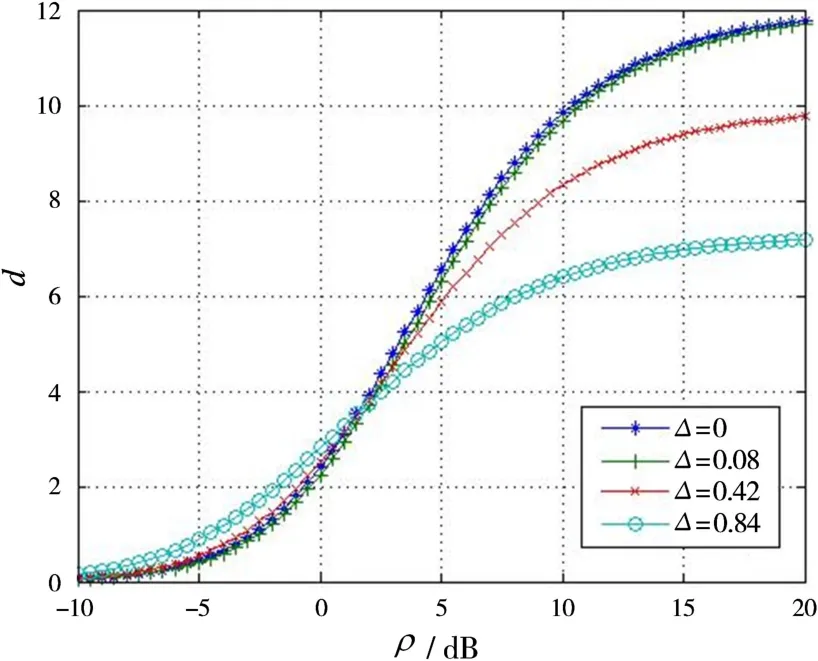
图5 参考信噪比与偏离系数的关系

文章研究了MIMO雷达信道间距离差异对检测性能的影响,研究表明MIMO雷达信道间距离差异会导致信道间信噪比的起伏,进而影响MIMO雷达系统的检测性能。在信道信噪比较低时这种影响较小,但随着信噪比的提高,这种影响较大,会导致检测性能严重下降。故MIMO雷达在进行天线布置时,既需要考虑增大天线间距来获得空间分集增益,又需要考虑增大天线间距所带来的目标探测时信道间的距离差异以及对检测性能的影响。研究结果对统计MIMO雷达的系统配置和实际应用具有参考价值。

[1]陈浩文,黎湘,庄钊文,等.多发多收雷达系统分析与应用[M].北京:科学出版社,2015:2-5.

[2]陈浩文,黎湘,庄钊文.一种新兴的雷达体制:MIMO雷达[J].电子学报,2012,40(6):1190-1198.

[3]FISHLER E,HAIMOVICH A,BLUM R,et al. Spatial Diversity in Radars:Models and Detection Performance[J].IEEE Trans on Signal Processing, 2006,54(3):823-838.

[4]汤俊,伍勇,彭应宁,等.MIMO雷达对空域Rician起伏目标检测性能研究[J].中国科学F辑:信息科学, 2009,39(8):866-874.

[5]何茜.MIMO雷达检测与估计理论研究[D].成都:电子科技大学,2010.

[6]廖羽宇.统计MIMO雷达检测理论研究[D].成都:电子科技大学,2012.

[7]CHELLAPPA R,THEODORIDIS S.Academic Press Library in Signal Processing,Volume 2:Communications and Radar Signal Processing[M].Oxford:Academic Press,2014:667-713.

[8]LIU Jun,LI Hongbin,HIMED B.Persymmetric Adaptive Target Detection with Distributed MIMO Radar[J].IEEE Trans on Aerospace and Electronic Systems,2015,51(1):372-381.

[9]SORIA F R C,GARCIA J S,BARBOZA F M M. Improved Detection of SM-SMux Signals for MIMO Channels[J].IEEE Latin America Transactions, 2015,13(1):43-47.

[10]LIU Su,ZHANG Gong,ZHANG Jiandong,et al. Transmit and Receive Gain Optimization for Distributed MIMO Radar[J].Wireless Personal Communications,2015,85(4):1969-1986.

[11]谷文堃,王党卫,马晓岩,等.分布式OFDM-MIMO雷达非相参积累目标检测方法[J].系统工程与电子技术,2015,37(10):2266-2271.

[12]谷文堃,王党卫,郑岱堃,等.分布式OFDM-MIMO雷达高速微弱目标多帧检测[J].华中科技大学学报(自然科学版),2016,44(2):65-69.

[13]王怀军,许红波,陆珉,等.MIMO雷达技术及其应用[J].雷达科学与技术,2009,7(4):245-249.

[14]马红星,陈思佳.水面杂波背景的统计MIMO雷达检测方法研究[J].雷达科学与技术,2015,13(5): 479-484.

[15]CHERNYAK V S.Fundamentals of Multisite Radar Systems:Multistatic Radar and Multiradar Systems [M].Boca Raton,FL:CRC Press,2011:25-36.

[16]RICHARDS M A.Fundamentals of Radar Signal Processing[M].New York:McGraw-Hill Education,2005:41-83.

[17]谷文堃,王党卫,彭尚,等.分布式OFDM-MIMO雷达包络对齐方法[J].华中科技大学学报(自然科学版),2014,42(10):19-24.

[18]BOX G E P.Some Theorems on Quadratic Forms Applied in the Study of Analysis of Variance Problems,I.Effect of Inequality of Variance in the One-Way Classification[J].Annals of Mathematical Statistics,1954,25(2):290-302.

[19]SCHARF L L.Statistical Signal Processing:Detection,Estimation and Time Series Analysis[M].2nd ed.New York:Pearson Education,2002.