基于OFDM的被动雷达目标检测方法∗

(国防科技大学电子科学与工程学院,湖南长沙410073)

0 引言

近年来,利用无线通信信号探测低空目标因低空安全威胁日趋严重而更加具有研究价值[1]。在现有通信体制中,正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术是继CDMA之后4G移动通信的核心技术[2],其主要优点包括频谱利用率高,抗多径性能好,可应用于大部分雷达体制[3-4]。

最近十年,国内外关于OFDM新体制雷达的文献时有报道,内容涵盖了波形设计、信号处理和OFDM新体制雷达系统构建等方面。在国内,国防科技大学、北京航空航天大学、电子科技大学、南京理工大学等单位都针对OFDM等无线通信信号的被动雷达技术展开了研究,如西安电子科技大学[5]提出了通信体制下的目标轨迹检测方法,湖南大学[6]将OFDM信号应用于车载被动雷达,实现通信雷达一体化,加强行车过程中汽车对周围情况的感知;叶映宇等[7]着重研究了被动雷达系统下的模型建立方法。在国外,美、德、法、以、荷、印等多个国家的大学和研究机构也开展了OFDM信号应用于被动雷达的研究工作,文献[8-9]研究了杂波环境下OFDM被动雷达的模糊处理方法,证明了OFDM信号在被动雷达运用中的优越性;文献[10]在先跟踪再检测的原则下,研究多目标背景下OFDM雷达被动联合检测跟踪的问题,提出一种递推贝叶斯滤波器;Arroyo等[11]针对被动处理SAR的WIMAX OFDM波形进行研究。武汉大学[12]将研究重点放在载波频偏对OFDM波形外辐射源雷达性能的影响,并得到结论:载波频偏会影响信号重构的误码率,并且影响时域杂波的抑制性能。

从以上文献看出,OFDM信号可应用于多种雷达体制,实现多样功能。但是,在目标检测方面,现有研究都依赖于目标高速运动带来的多普勒频移来完成探测。其中Van Beek提出的基于循环前缀的最大似然估计算法(MLE)[13]最为基础,许多估计算法都是在此算法上加以改进,鲜有针对慢速目标的方法;在波束形成方面,2006年以来,国内开始掀起OFDM信号下的数字波束形成(Digital Beam Forming,DBF)的研究热潮,文献[14]研究了多径背景下无源雷达DBF的效果和影响因素,证明了量化分析方法可以减弱多径的不利影响;文献[15-17]针对被动雷达提出两种典型的空时域滤波方法,一种是多波束扫描可等效于用宽波束覆盖照射区域,既可以保证方位分辨率,又可以解决时间和空间的覆盖要求,另一种是建立三维匹配滤波函数,同时进行时间、径向距离和角度的三维匹配滤波。第一种方法对接收阵列参数可能造成的影响缺乏深入研究,第二种方法计算量大,不利于对目标的实时检测。

本文利用OFDM信号覆盖广、抗多径性能好等优点,将其应用于城市背景中的低空慢速目标探测,在移动通信中的IEEE 802.11p协议下提出一种低空慢速目标探测方法,具有低费效比和高探测性能的优点。

1 接收阵列模型及数字波束形成方法

1.1 被动雷达接收阵列

为了实现空间上的全方位覆盖和二维探测,本文选用均匀圆阵作为接收阵列。在阵列信号处理理论中,与均匀线阵和传统的平面相控阵相比,圆阵天线有着独特的优越性,包括以下几点:

1)均匀圆阵可以在阵列平面形成无方向性、形状对称的方向图函数;

2)均匀圆阵具有远场模式与频率无关的特点,可以应用于宽带、超宽带信号体制,符合OFDM信号多路载波合成宽带的特点;

3)当阵元数不少于16时,均匀圆阵能提供360°方位角覆盖,实现90°俯仰角的扫描,在扫描过程中能维持或基本维持天线波束的形状和增益。

1.2 均匀圆阵的方向图函数

根据数字波束形成理论,阵列方向图函数表示为权矢量与信号入射角的关系。阵列幅度方向图函数是方向图函数的模,其数学表达为

式中,a(α)为阵列波束方向矢量,vH为权矢量v的Hermite矩阵。为了能使波束主瓣指向回波方向αi,k,各个阵元就要在αi,k方向上同向相加,数学表达即v=a(αi),此时输出方向上的增益最大。如图1所示,模型在球坐标系中讨论,方位角为θ,俯仰角为φ,是相对于z轴的正向夹角。

图1 系统坐标系以及几何关系

设置均匀天线圆阵,建立球面坐标系(r,θ,φ),假设接收阵列为阵元数量为M的均匀圆阵。接收天线均匀分布在半径为r0的圆上,将方位角为0°的天线命名为E k1,逆时针转动依次命名为E k2至E kM。每个阵元的权重为v1,v2,…,v M,每个阵元的方位角如果来自某一方向(θ,φ)的平面波照射到圆形阵列天线上,则每个天线相对于阵元中心的相对相位为

所以圆形阵列的方向图函数为

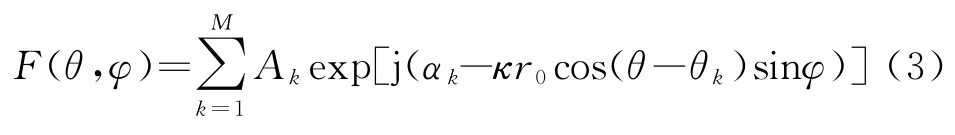
即可得到相应的方向图函数表达式:

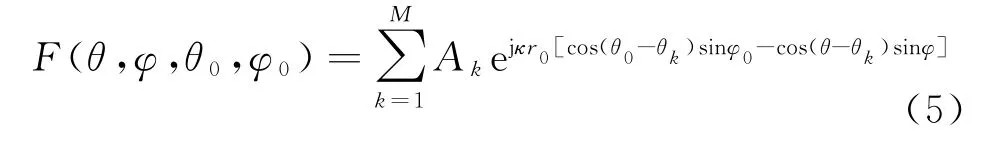
采用分平面分析的方法。如果只关注圆形阵列所在平面,即俯仰角全部取90°,方向图函数变为二维单变量函数:

若只关注圆形阵列所在平面的某一法平面,即所有方位角全部取0°,方向图函数变为另一种形式的二维单变量函数:

将基于方位角的方向图函数和基于俯仰角的方向图函数结果进行综合,就可以得到三维球坐标系下的目标角位置(θ0,φ0)。若每一天线阵元的各项参数均相同,则A k=1。

2 基于改进的CFAR检测器的低空目标检测方法

2.1 OFDM信号的目标回波模型

OFDM通信信号的表达式为

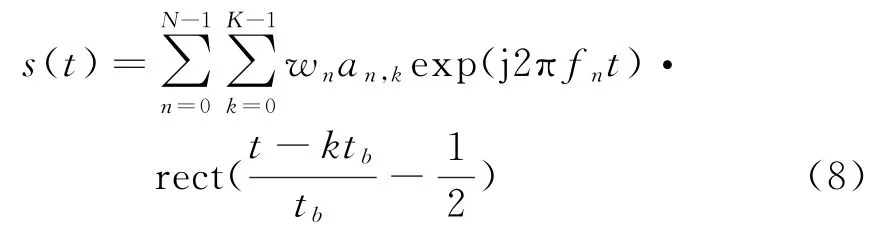
式中,N为子载频数,K为相位编码长度,w n= |w n|ex p(jφn)为第n个子载频的加权系数,a n,k=exp(jθn,k)为第n个子载频上码元k相位编码,f n=f0+nΔf为第n个载频的中心频率。各路子载频正交,需满足

正交性可以保证信号对空间的全向辐射。在第n个子载频上的对第i个目标的多普勒频移为,第i个目标的后向散射系数为σi,引起的单程时延为τi。回波信号可以表示为

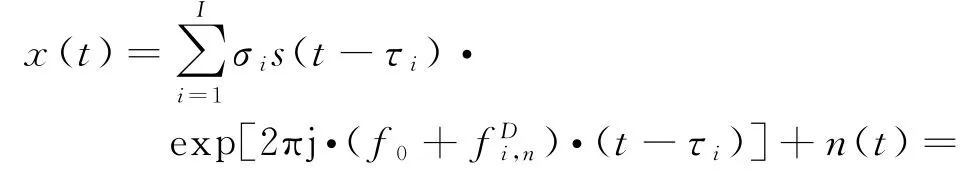
在单目标的情况下,回波信号可以化简为

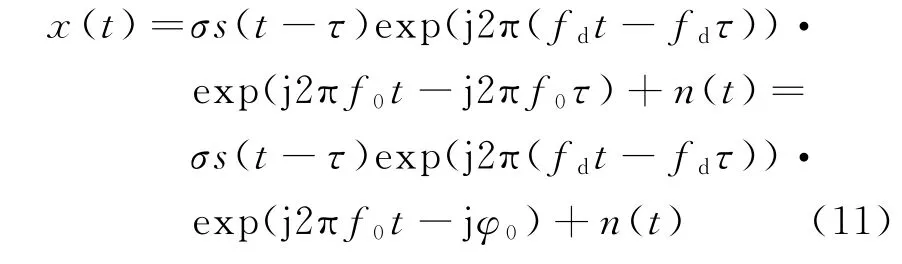
式中,φ0为时延引起的载波相位变化,n(t)为高斯白噪声,fd为目标运动引起的多普勒频移。因为时延引起的多普勒相移非常小,回波信号经过下变频至基带以后,可以表示为

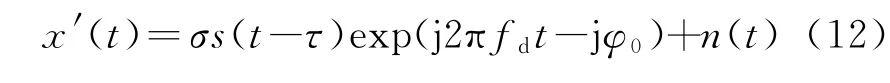
2.2 基于循环前缀的OFDM高分辨脉冲压缩

循环前缀(Cyclic Prefix,CP)是OFDM通信中的重要概念,可以理解为保护间隔的一种。OFDM信号生成之后,在送入信道传输之前,依靠添加CP的方式来保证无码间串扰的发生。其长度必须大于信道的最大时延。CP就是在每个OFDM符号之前插入其尾部的若干个采样值,其结构示意如图2所示。

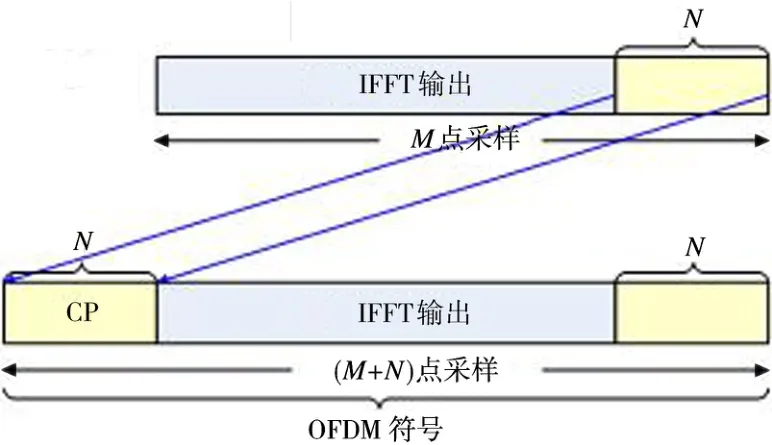
图2 OFDM符号添加CP示意图

可见CP可将信道与信号之间的线性卷积变为圆周卷积,消除码间串扰和OFDM符号间干扰。CP也会带来一定的性能损失:其一,在接收端解调时删除CP造成了发射信号能量的浪费;其二,传输循环采样点会降低系统的频带利用率。因此,在OFDM通信系统中,CP长度控制在OFDM符号长度的25%以下,根据信道最大时延不同一般选择25%或12.5%的比例。

优化处理后的回波信号经过采样作为输入进入脉冲压缩模块,经过匹配滤波处理后可输出目标的一维距离像。假设基于OFDM信号多载频的结构特点,在接收端先对回波信号作子载频分离,再分别解码,对子载频内解码的结果与原始编码作卷积,得到一次脉压粗分辨距离像;接着再合成粗分辨距离像单元,得到二次脉压高分辨距离像。但是传统的二级脉冲压缩有严重缺陷:由于信道延迟的作用,每个码元后移,观测区间内不再包含整数倍码元,而是发生错位,造成解码错乱。

如图3所示,假设接收到信号之后不去除CP,对于将进行信号处理的任一码元段,只要保持分段后的“码元”(此时并不代表真正的码元,而是与调制端的码元对应的概念)总长度依然为M+N,那么无论观测区间怎么取值,都能够保留所有码元中的所有目标信息,利用DFT解码的时候无错乱。

图3 基于CP的接收信号示意图

2.3 自适应均值类CFAR检测算法

一般情况下,直达波分量会“淹没”目标回波,地面目标反射的多径分量也是一种很强的干扰。采用恒虚警检测(Constant False Alarm Rate, CFAR)保证雷达在强干扰下正常工作。

瑞利杂波背景下的均值类CFAR检测方法包括单元平均恒虚警检测器(CA-CFAR)、单元平均选大恒虚警检测器(GO-CFAR)和单元平均选小恒虚警检测器(SO-CFAR)。CA-CFAR只在均匀杂波环境下具有最优的检测性能;GO-CFAR具有抗杂波边缘的能力,而SO-CFAR适用于多干扰目标的杂波环境。结合低空慢目标的特点和3种均值类CFAR的优点,提出一种新的自适应均值类恒虚警算法(AM-CFAR)。

如图4所示,回波信号通过脉冲压缩以后,再通过平方律检波器后获得采样序列,若检测单元为V,选择检测单元左右两侧长度为W的邻域计算杂波功率估计值然后分别与标称化因子T相乘,得到和的值不相等,从中选择与检测单元V的值相近的那一侧作为检测门限;若和的值相等,则从中任意选取一侧作为检测门限。

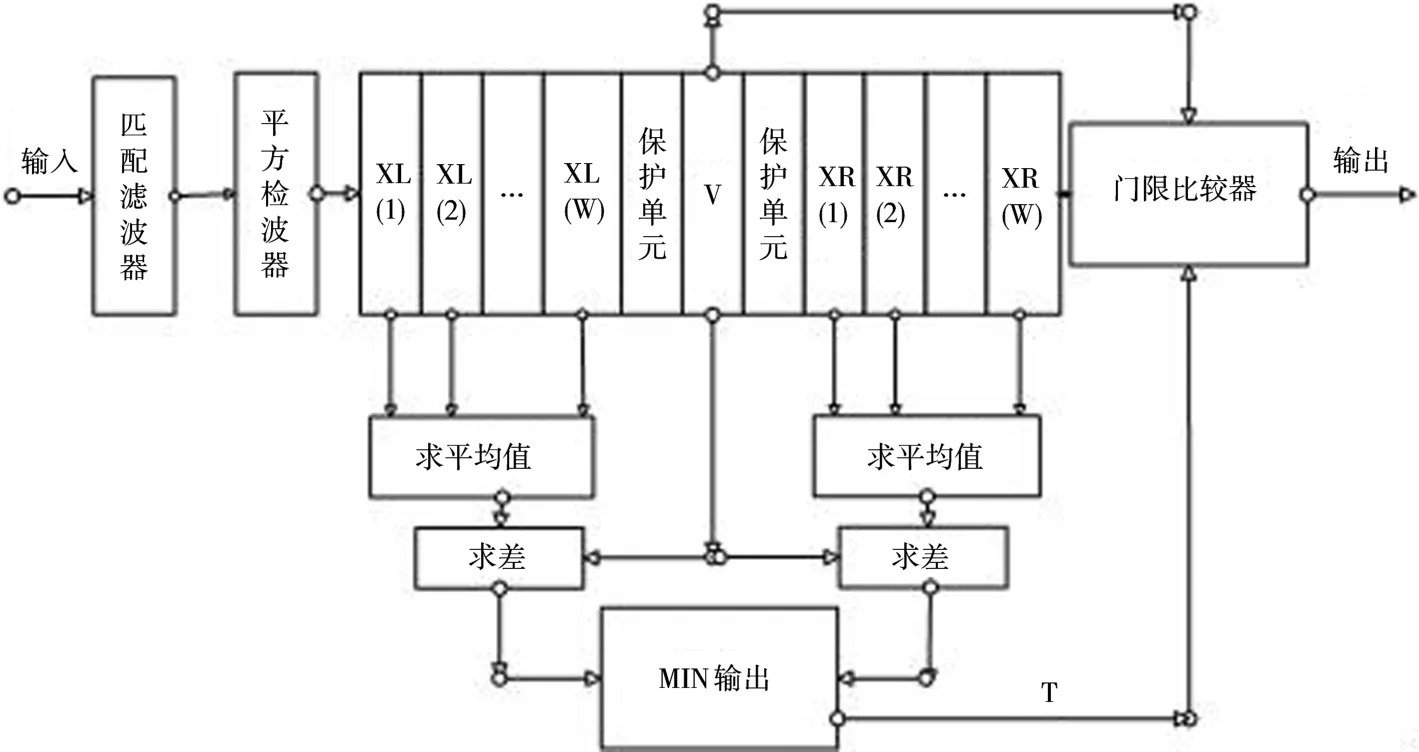
图4 AM-CFAR流程图

从AM-CFAR的检测原理可以看出,当两侧杂波功率估计值不相等时,若检测单元V的值与中较大的一个接近,则选取作为检测门限,此时AM-CFAR算法等同于GO-CFAR算法;若检测单元V的值与中较小的一个接近,则选取作为检测门限,此时AM-CFAR算法等同于SO-CFAR算法;当两侧杂波功率估计相等时,则选取中任何一个作为检测门限,即门限的取值为此时AM-CFAR算法等同于CA-CFAR算法。综上所述,AM-CFAR算法可以根据杂波功率估计值的大小自适应地选择最值或均值作为检测门限,一方面结合了传统CA-CFAR的抗杂波性能、GO-CFAR的抗杂波边缘能力和SO-CFAR在多目标情况下的适应性,能够极好地结合应用背景;另一方面比GO-CFAR与SO-CFAR恒选大和恒选小原则更加灵活。

3 系统处理流程

低空目标探测系统的信号处理流程如图5所示。回波信号被天线阵列接收后作为输入送入数字波束形成模块和接收机保护器。回波信号在经过高频低噪声放大器之后,只有与基带信号混频才能降为中频,因而得到最大的输出信噪比。脉冲压缩模块将目标的径向距离信息一部分送入结果综合模块储存;另一部分以序列的形式送入平方律检波器作恒虚警检测,从极低的信噪比中检测出被“淹没”的目标,结果也送入结果综合模块储存。

另一方面,数字波束形成的结果合并方位向和俯仰角的信息,送入结果综合模块储存。结果综合模块就可以得到具有径向距离、方位角、俯仰角的三维目标信息。

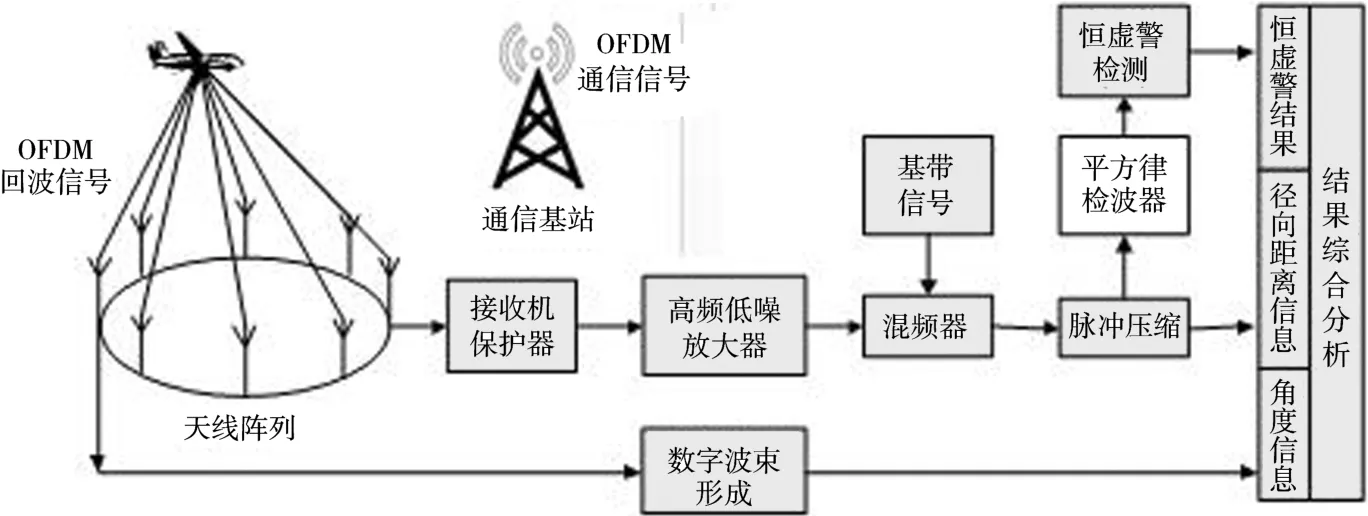
图5 系统信号处理流程图

4 仿真实验与分析

4.1 均匀圆阵方向图综合特性

为了保持均匀圆阵的对称性,一般将天线阵元的个数取定为4的倍数。阵元数不少于16时,均匀圆阵能提供360°方位角覆盖,实现90°俯仰角的扫描。兼顾系统复杂程度,将天线阵元的个数设为16。

仿真中阵列天线与目标的相关参数设置如表1所示。

表1 接收阵列天线参数

图6仿真了在方位角为120°、俯仰角为30°、阵列半径为λ的三维方向图特性。此时方向图有最大的“零陷”,波束形成特性最优;分别从方位角和俯仰角平面分析,该圆阵基本形成对方位角为120°、俯仰角为30°的方向对准。但是俯仰角平面的DBF峰值平坦,性能不理想。

图6 均匀圆阵的三维方向图函数

4.2 基于OFDM二级脉冲压缩的性能分析

根据中国移动公司基于LTE的4G通信环境的频段参数,利用OFDM信号进行仿真,表2给出此标准下的一些参数设置。

表2 中国移动公司4G试验频段下的OFDM参数

上行链路即移动台发基站收,下行链路即基站发移动台收,根据应用背景,选取下行链路2 350 MHz作为中心载频进行仿真。设探测区域[500,1 000]m内共有3个静止目标,与雷达的径向距离分别是{650,800,920}m,后向散射系数分别为{0.5,1,0.8},以分析直接脉冲压缩和分码元二级脉冲压缩所得的一维距离像的性能。图7的结果表明:1)分码元二级脉冲压缩(线条)在680 m, 830 m,950 m处的“伪峰”严重干扰了测距结果; 2)因为仿真的是归一化一维距离像,可以看出直接脉冲压缩(点迹)的主瓣能量分散,峰值功率低,旁瓣高,而分码元二级脉冲压缩性能更好。

由仿真结果看出,中国移动公司4G试验频段下的高载波频率保证了良好的目标回波特性。脉冲压缩得出的目标一维距离像结果与设置的目标位置基本拟合。

为了进一步说明3种脉冲压缩方法对相近目标的分析性能,设探测区域[630,700]m有3个静止目标,径向距离是{650,655,657}m,后向散射系数是{0.5,1,0.8}。图8表明直接脉冲压缩与基于CP的二级脉冲压缩得到的目标一维距离像基本相同,去除CP后的脉冲压缩结果为{680,685, 687}m,伪峰超过真实位置,测距结果错误。

图7 目标的一维距离像

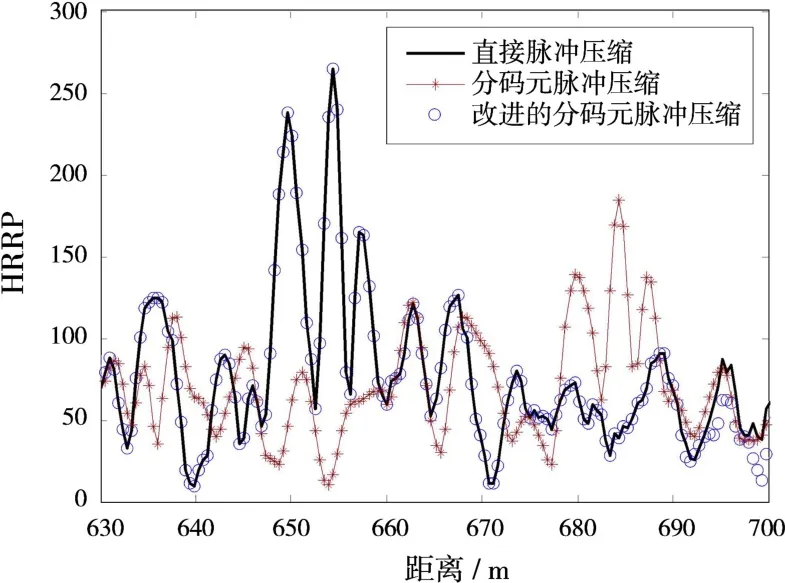
图8 3种脉压方法对相近目标的探测性能对比

4.3 基于改进的CFAR检测器的低空目标检测

图9是SNR=0 dB时虚警率Pfa=0.001、参考单元数为32、保护单元长度为3的GO/SO/CACFAR三种均值类CFAR算法性能对比。GOCFAR算法下的门限明显比以上3种均值类CFAR算法的门限提高了,意味着有漏警的可能性,但是也大大降低了虚警的风险。抗杂波边缘的能力在第一个目标散射点前后门限中体现得较为明显,在进入参考单元序列后,门限先陡峭抬高,避免虚警,再平缓降低;同时,保护单元的长度即图中目标前后“碗口”的大小,因此保护单元的长度如果过长,可能会导致对信号信息不必要的浪费。以往研究指出,保护单元长度在参考单元长度的10%左右较为合适。

图10是相同条件下AM-CFAR对3个目标回波的检测效果,说明AM-CFAR对微弱目标(SNR=0 dB)有优良的预警效果。当且仅当所有目标都被检测出来才记为有效,表3列出SNR=0 d B时不同Pfa通过250次、1 000次和5 000次蒙特卡洛实验得到的AM-CFAR的检测概率Pd。可以看出,检测概率Pd在不同恒虚警率下能够保持在90%左右。

图9 3种均值类CFAR算法仿真

图10 AM-CFAR对微弱目标的检测效果

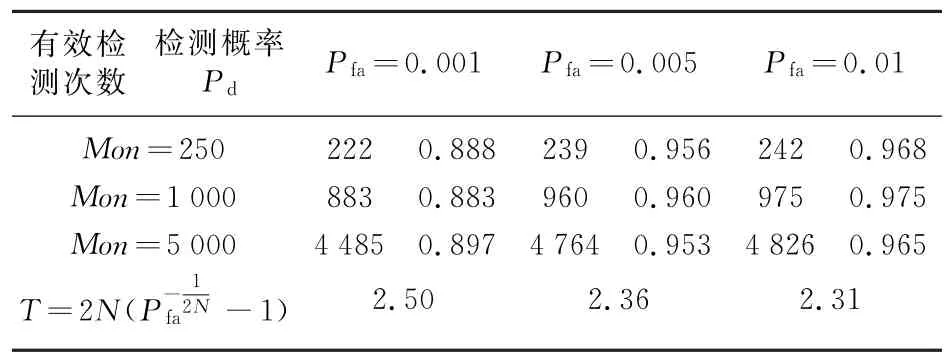
表3 不同蒙特卡洛试验下的检测概率

5 结束语

本章以经过优化处理后的OFDM信号为分析基础,通过信号处理提取出其中包含的角度、径向距离等信息,然后将脉冲压缩结果输入改进的AM-CFAR检测器,检测到弱目标。信息的提取和处理方法综述如下:利用圆阵方向图函数特性确定阵元个数为16;接着仿真球坐标系下的三维方向图函数证明其可以形成对方位角和俯仰角的波束;为了充分利用OFDM信号的结构特点,以直接脉冲压缩效果为基准,提出分码元二级脉冲压缩方法和基于CP的二级脉冲压缩方法,前者因解码错乱易造成一维距离像的“伪峰”,后者能够合成一维高分辨距离像。AM-CFAR检测器以匹配滤波结果为输入,检测概率Pd能够保持在90%左右。仿真实验验证了方法的有效性。但还有许多研究内容,例如杂波抑制、多径效应消除等,需要在下一步工作中逐步开展。

[1]SEN S,NEHORAI A.Adaptive OFDM Radar for Target Detection in Multipath Scenarios[J].IEEE Trans on Signal Processing,2011,59(1):78-90.

[2]顾陈,张劲东,朱晓华.基于OFDM的多载波调制雷达系统信号处理及检测[J].电子与信息学报,2009, 31(6):122-132.

[3]WU X H,KISHK A A,GLISSON A W.MIMOOFDM Radar for Direction Estimation[J].IET Radar,Sonar and Navigation,2010,4(1):28-36.

[4]SEN S,TANG G,NEHORAL A.Multiobjective Optimization of OFDM Radar Waveform for Target Detection[J].IEEE Trans on Signal Processing, 2011,59(2):639-652.

[5]白建雄.基于CDMA信号的外辐射源雷达弱小目标检测技术[D].西安:西安电子科技大学,2014.

[6]周明千.OFDM雷达通信一体化系统中的数字波束形成技术研究[D].长沙:湖南大学,2014.

[7]叶映宇,文铁牛,陈俊,等.外辐射源雷达运动目标信号特性及检测方法研究[J].雷达科学与技术,2014, 12(6):604-607.

YE Yingyu,WEN Tieniu,CHEN Jun,et al.Characteristics and Detection of Moving Target Signal of Radar System Based on External Radiation Source[J]. Radar Science and Technology,2014,12(6):604-607. (in Chinese)

[8]KAUFFMAN K,RAQUET J,MORTON Y,et al. Real-Time UWB-OFDM Radar-Based Navigation in Unknown Terrain[J].IEEE Trans on Aerospace and Electronic Systems,2013,49(3):1453-1466.

[9]SEARLE S,PALMER J,DAVIS L,et al.Evaluation of the Ambiguity Function for Passive Radar with OFDM Transmissions[C]∥IEEE Radar Conference, Cincinnati,Ohio,USA:IEEE,2014:1040-1045.

[10]LEH MANN F.Recursive Bayesian Filtering for Multitarget Track-Before-Detect in Passive Radars [J].IEEE Trans on Aerospace and Electronic Systems,2012,48(3):2458-2480.

[11]GUTIERREZ A J R,JACKSON J A.WiMAX OFDM for Passive SAR Ground Imaging[J].IEEE Trans on Aerospace and Electronic Systems,2013, 49(2):945-959.

[12]ZHAO Zhixin,WAN Xianrong,XIE Rui,et al.Impact of Carrier Frequency Offset on Passive Bistatic Radar with Orthogonal Frequency Division Multiplexing Waveform[J].Journal of Electronics&Information Technology,2013,35(4):871-876.

[13]LELLOUCH G,MISHRA A K,INQQS M. Stepped OFDM Radar Technique to Resolve Range and Doppler Simultaneously[J].IEEE Trans on Aerospace and Electronic Systems,2015,51(2): 937-950.

[14]JIANG JUN,HAO Zhimei,XIONG Wei.Study on New Monopulse Angle Estimation Method Base on Adaptive Digital Beamforming[J].Computer Simulation,2011,28(2):18-21.

[15]王晓辉,张曙,黄蕾.自适应波束形成技术在OFDM系统中的应用与仿真[J].应用科技,2008,35(11): 19-22.

[16]黄永明,杨绿溪.空时编码OFDM与多维波束形成组合方案[J].通信学报,2006,27(9):129-134.

[17]吴莉莉,尚勇,梁斌,等.有频偏的OFDM信号的抗干扰迭代式接收机[J].电子与信息学报,2006,28 (11):2103-2106.