基于参数预估计和滑动FFT的MFSK信号类内识别方法*
张华娣,楼华勋,2
(1.中国电子科技集团公司第三十六研究所,浙江 嘉兴 314033;2.通信信息控制和安全技术重点实验室,
浙江 嘉兴 314033)
0 引言
随着无线通信技术的发展,电磁频谱环境日益复杂,有效识别不同调制方式的通信信号在军事电子对抗和民用频谱监测领域都具有重要的应用前景[1]。多进制频移键控(M-ary Frequency Shift Keying,MFSK)信号为载波频率随码元变化的非平稳信号[2]。对MFSK信号的识别,特别是对调制指数较小情况下的MFSK信号的类内正确识别一直是通信调制方式自动识别研究领域的热点和难点问题。文献[3]利用信号过零点的时间间隔和其差分序列,对码元跳变点处的信息进行直方图统计实现对频移键控(Frequency Shift Keying,FSK)类内识别。文献[4]利用瞬时频率直方图峰数进行MFSK类内识别。文献[5]提出利用经小波变换后的幅度层数对MFSK 进行类内识别。文献[6]提出利用时频脊线提取FSK信号特征,并将减法聚类和模糊C均值聚类(Fuzzy C-Means clustering,FCM)算法相结合,实现MFSK信号调制类型的自动分类。文献[7]根据归一化前后小波变换包络之间的差异性,提出了基于小波变换系数差值、小波相似度特征参数的算法,实现了数字信号调制方式的识别。这些方法在调制指数较小,信噪比较低的情况下识别正确率不高。受文献[8]基于滑动快速傅里叶变换(Fast Fourier Transform,FFT 这个FFT 在摘要中已经出现过)的快速相关检测算法的启发,本文从工程实用角度出发,提出了一种基于参数预估计和滑动FFT的MFSK信号的类内识别方法。该方法首先估计出MFSK信号的码元速率,并找到码元的起始点;其次运用计算出来的码元宽度和码元起始信息作为先验知识,对输入信号进行滑动FFT 处理,并计算各个码元的频率值;最后对所有频率值进行归并统计,按照频率值种类数来实现MFSK信号的类内识别。
1 调制指数对识别的影响分析
频移键控信号的瞬时频率携带着基带信息,并在码元跳变处发生变化,其一般表达式为:
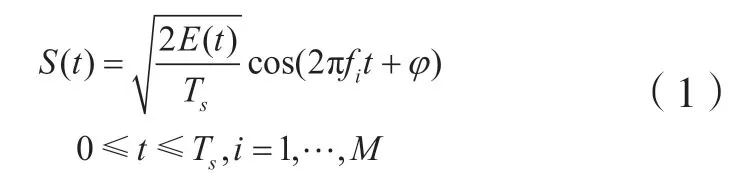
式中:Ts为符号周期;fi为信号的瞬时频率;M为离散值个数;E为码元能量;、φ分别为信号的幅值和相位,是任意常量[9]。
如果M=2,则称该FSK信号为二进制FSK(2FSK)。此外,FSK的一个重要参数是调制系数h。设两个载频分别为fc1和,定义h=(2Δf)/fb,其中,Δf为信号频偏,等于,而fb为信号的符号速率[10]。
推而广之,MFSK信号的调制指数h定义中的Δf等于最大频率和最小频率的差值的一半[11]。由调制指数的定义可知,当信号的符号速率一定时,信号的频偏越小,则调制指数越小;当信号的频偏一定时,信号的码元速率越大,信号的调制指数越小。
下面分析调制指数对识别的影响。当信号的符号速率一定时,信号的频偏越小,则调制指数越小,而当频率偏差小的时候,瞬时频率会靠得很近。如果在噪声情况下,相近的瞬时频率就会被当成一个频率,从而造成错判以及误识别。当信号的频偏一定的情况下,信号的码速率越大,则信号的码元宽度就越小,信号频率跳变的速率就越高,也就是说某个频率累积的时间就越短,累积的能量就越低,不利于信号的检测。因此调制指数越小,MFSK信号的识别难度就越大。
2 识别算法
2.1 码速率估计
码速率是数字调制信号区别于模拟调制信号的一个重要特征,其正确估计在非协作通信中有着极为重要的意义[12]。理论分析表明单极性随机脉冲序列的功率谱在码元速率fs的整数倍处存在离散谱线[13],只要通过适当地变换构造同符号速率的单极性脉冲波形,再对其进行谱分析就可以估计到信号的符号速率。文献[14]提出了一种详细的计算FSK信号的码速率的方法,先得到瞬时频率,再对瞬时频率进行Harr 小波变换,然后通过对单极性成形脉冲进行FFT 变换,就可以通过寻找频谱最大值点计算出FSK信号的码速率。
该方法同样可以应用到MFSK信号中,只要是MFSK 类信号就可以用该方法进行计算,而不需要先确定MFSK的M值。
2.2 码元同步头估计
2.1 节介绍了码元速率的估计,本节利用码元速率作为已知预估计参数。由式(1)可知,由于MFSK信号的一个码元宽度内只有一种频率,因此,用一个码元宽度内的信号做FFT 处理。如果信号完全在一个完整的码元内,相应的FFT 可以得到幅度最大的频谱值;如果做FFT的信号点跨越了两个码元,并且这两个码元的频率值不一样的情况下,做FFT 时两个频率的频谱幅度值都达不到最大值。因此,可以通过检测某一个频率的最大幅值来确定所采集的信号是在一个完整的码元内,从而确定码元的起始点。具体做法为:
(1)接收信号内从接收的起始时刻开始,取一段与码元宽度等长的信号窗口,并向后逐点滑动该信号窗口,滑动距离不超过一个码元宽度;
(2)对窗口内的信号做FFT 运算,记录每次FFT 运算的频谱峰值以及共滑动的点数;
(3)比较每一次滑动的FFT的谱峰值,找到谱峰最大点值,则其对应的信号点为码元起始点。
2.3 滑动FFT 求各码元频率及判别
在码元速率和码元起始点作为已预估参数的情况下,可以精准地对每个码元的信号进行频率估计,具体步骤如下文所述。
(1)做一次粗略的频谱估计,在采样率较高、频谱较宽、频谱分辨率较低的情况下,估计该MFSK信号的带宽。
(2)根据粗略估计的MFSK信号频谱宽度,重新设置一个相对较低的采样速率;根据重新设置的采样速率,计算每个码元的采样点数。此外,为了方便使用FFT 进行计算,重新设置了采样速率之后,应使每个码元的采样点数为2的幂次方。
(3)以码元起始点开始,每个码元内信号做一次FFT,并求出每个码元信号的频谱。
(4)这样可以得到所采样数据内对应的与码元个数相等的频谱峰值,并根据这些频谱峰值计算相应码元的信号频率,统计出总共有几种频率值。
(5)最后,根据M/2~M个峰判定为M 阶FSK的原则,即1~2 个频率种类,判定为2FSK,3~4个频率种类判定为4FSK,5~8 个频率种类判定为8FSK,从而完成对MFSK信号的类内识别[15]。
3 实验结果及分析
实验中,以2FSK、4FSK、8FSK为例,在0~20 dB信噪比下进行了1 000 次蒙特卡罗仿真实验,码元数为1 000,符号速率为16 sps,采样频率为128 Hz,最小频率偏差8 Hz。信噪比为5 dB 时的测试结果如表1 所示。

表1 识别概率统计表 %
对于2FSK、4FSK、8FSK信号,为了便于对比直接用小波变换后的幅度层数对MFSK信号进行识别的效果和本算法进行识别的效果,将两种算法识别概率随信噪比变化的曲线绘制在同一图上,如图1 所示。其中,参数设置为:码元数为1 000,符号速率为16 sps,采样频率为128 Hz,最小频率偏差8 Hz。虚线部分为本算法识别概率随信噪比变化的曲线,实线为用小波变换后的幅度层数对MFSK信号进行识别的算法识别概率随信噪比变化的曲线。

图1 不同信噪比下两种算法的正确识别率对比曲线
由图1 可以看出,在高信噪比情况下,比如信噪比大于17 dB 时,两种算法没有明显的区别。当信噪比较低时,新算法对MFSK 调制信号的识别概率大大提高,本文提出的算法明显优于直接用小波变换后的幅度层数对MFSK信号进行识别的算法。此外,本算法无须任何先验知识,提高了MFSK信号类内识别的概率,特别是在调制指数较小,低信噪比情况下信号的识别性能得到了明显改善。
4 结语
本文提出了用预估参数和滑动FFT 对MFSK信号进行类内识别的方法。该方法充分利用MFSK信号码元速率求取方法一致的特点,先进行码元速率估计,再根据预估参数和滑动FFT 处理进一步完成信号类型的判别。这种处理方法把预估参数作为先验知识进行信号处理,能设置最优的采样率和合理的FFT 长度进行处理,因此,在调制指数较小,信噪比较低的情况下也能完成信号的正确识别,这正是信号侦测应用中所期望达到的效果。

