顺应学生的认知规律 突出概念的形成过程

朱希萍

摘 要：概念教学应把握学生学习起点，顺应学生的认知规律，突出概念的形成过程，注意语言的外部输入，注重知识的动态变换，理解概念的本质。

关键词：小学数学；认知规律；形成过程；动态变换；概念本质

中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2015）14-0057-04

概念是反映事物本质属性的思维形式。小学数学教学中，有关的概念共有五百多个，包括九大类：数的概念、几何形体的概念、量与计量单位的概念、数的整除性概念、简易方程的概念、比和比例的概念、运算的概念、应用题、数量关系的概念。

数学概念一般比较抽象，对于以具体形象思维为主要形式的小学生来说学习起来不易掌握。在小学数学中，学生计算能力和解决问题能力的提高，空间观念的形成，逻辑思维能力的培养，都必须在加强概念教学的基础上进行。因此，重视数学概念教学，对于提高教学质量起着举足轻重的作用。

一、把握学生的学习起点，发挥学生的学习潜能

学习起点是指学生学习新内容所必须具备的知识及能力储备。它可分为学习的逻辑起点与学习的现实起点 。

现代建构主义理论认为，学习者学习数学并不是由教师或其他人传授给他的，而是他本人主动根据已有的数学经验、认知结构进行的一种主动建构的过程。学习者对新知识进行同化或顺应时需要经历一个由“平衡—不平衡—平衡”的螺旋上升的认知结构重组的过程，教学要充分建立在学生学习起点上。

比如，在教学“百分数的意义与读写”时，一位教师开门见山在黑板上写了“80%”，问学生见过它吗？结果这一班的学生都说见过，并能读出“百分之八十”。接着这位教师又问，在平常生活中什么时候用到过80%，能举一个例子吗？能画一个图表示80%吗？结果发现有部分学生能根据自己在生活中所了解到的，对这一百分数进行解读；而且大部分学生能画图表达自己对它理解。

以上教学教师就抓住学生的学习起点，并利用学生自己提供的具体素材进一步引导学生质疑、概括、提升，达到对百分数的初步理解。

二、突出概念的形成过程，顺应学生的认知规律

小学生建立数学概念往往有两种基本形式：一是概念形成，二是概念的同化。由于小学生的思维特点处于由形象思维向抽象逻辑思维过渡的阶段，因此，小学生学习数学概念大多以“概念形成”的形式为主。数学概念的形成要让学生经过直观感知、建立表象，顺应学生的认知规律，突出数学思维过程。

三、注意语言的描述，加强概念的外部输入

数学概念是数学思维的主要元素，数学概念的最终表征是通过语言进行。数学概念的形成、内部表征、外部运用、数学概念之间的联系建立、整个概念网络的建构，都是通过数学语言来完成。因此，数学语言在数学概念的形成中起着举足轻重的效果。教学中每一教学活动都力求从学生已有的语言出发，对所进行的活动进行解释、建构，将概念的形式化语言内化为学生的自我语言。这样概念的过程转化为对象，概念的结构才有了依附。

例如，在教学“平行与垂直”时。

（一）第一步：研读文本，尝试画图

引导学生自学，并尝试画出图形。

师：今天我们要研究两条直线的特殊位置关系，板书课题“平行与垂直”。请同学们根据以下的提示先进行独立学习，再在小组中交流。

温馨提示：

①认真阅读课本（第56～57页），什么叫平行线和互相平行，什么叫互相垂直和垂线？请你在书上划出来。

②按你自己的理解，用水彩笔在两张白纸上分别画出两条直线互相平行和两条直线互相垂直。

③请同学们先在小组里说一说什么是互相平行？什么是互相垂直？并互相检查你们画的两条线是不是互相平行或互相垂直？

④各小组选出你们认为画出的是互相平行、互相垂直的作品准备作全班汇报。

（二）第二步：交流成果，质疑辨析

1.让学生根据自己的理解来说一说怎样的两条直线是互相平行？怎样的两条直线是互相垂直？

2.教师针对以上温馨提示组织学生反馈。

小组内说说：你们小组认为画出的两条直线是互相平行的请贴到黑板的左边区域，认为画的是互相垂直的贴到黑板的右边区域。

3.组织学生进行质疑辨析。

师：对于以上这么多的作品你们有什么想说的吗？

学生通过整体观察，再次在小组中交流自己的想法。然后教师组织集体说想法。

以上教学引导学生自觉观察、分析辨析概念的各种属性，并用自己的语言不断地进行辩说，使概念的各种表征与语言融为一个有机整体。

四、注重概念的动态变换，理解概念的本质特征

学生从概念原型中获得概念的标准属性，获得概念的表象与中心形象。变式有利于剔除概念直观材料、样例中的各种非本质属性，使学生对本质属性的认识得以深化。

在教学“三角形认识”时，通过以下变式帮助学生理解概念。

1.通过下图一组三角形的画指定底上的高。引导学生观察发现直角三角形直角边上的高就是另一条直角边。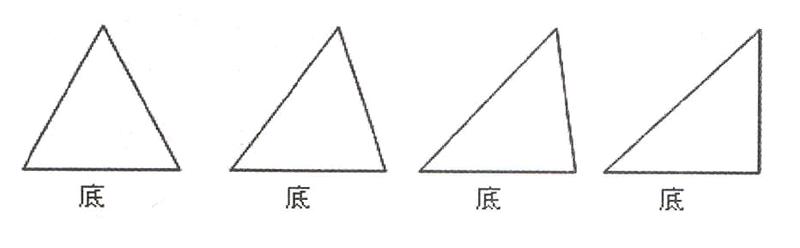

再利用投影动态演示随着三角形顶点的移动，从锐角三角形逐步变成直角三角形，使学生发现底上的高逐步在移动，当三角形变成直角三角形时，直角边上的高就与另一条直角边重合。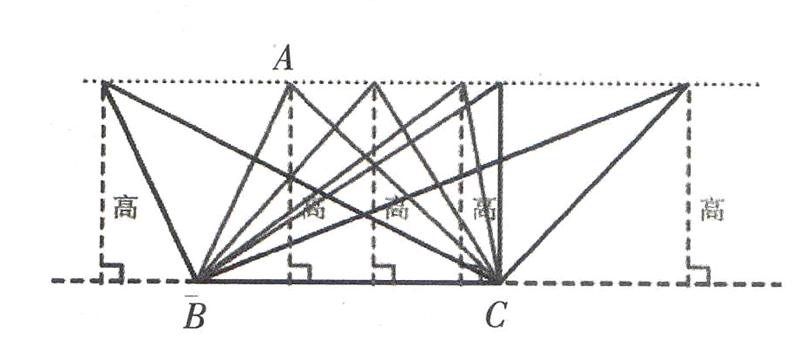

2.从以上的动态图中留下一条高，如图，让学生明确一端是一个三角形的一个顶点，一端是与底边垂直的垂足，并提出：你能通过这条高想象出一个三角形吗？请根据你的想象重新画出这个三角形吗？

针对学生所画的三角形组织学生质疑、评价。

3.利用课件演示变换中的三角形高的画法（如下图）。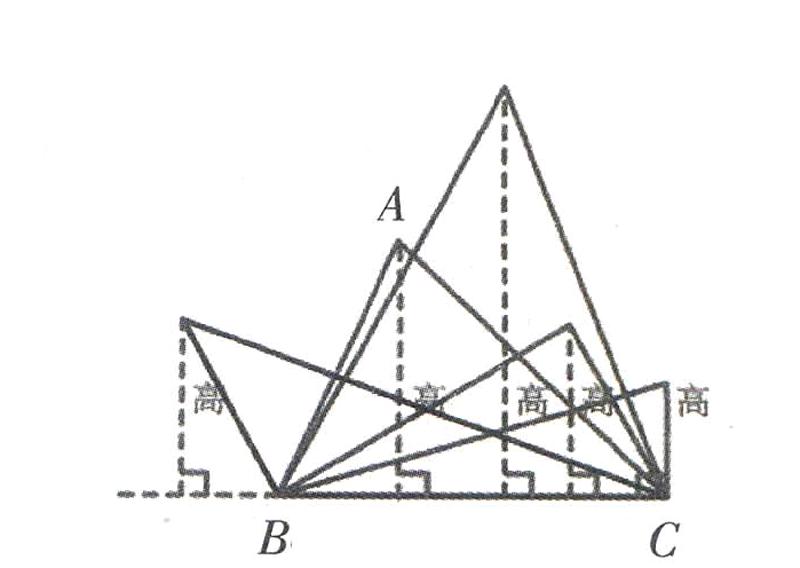

再向学生提出：我们对从上往下画高可能比较熟练，那你还能快速地画出下面每一个三角形指定底上的高，比一比。

利用投影检验学生所画的高是否正确。

以上教学，教师深入解析概念的本质属性与可能出现的非本质属性，精选中心样例、精心设计变式、时刻抓住对原型与变式的分析，不断形成对概念本质的深层理解。

总之，概念教学应根据学生的真实起点，顺应学生的认知规律，充分利用语言外部输入与思维的内部激发，让学生真正理解概念，掌握概念本质。