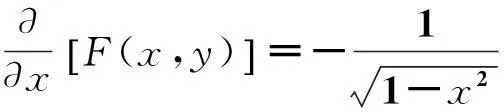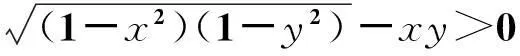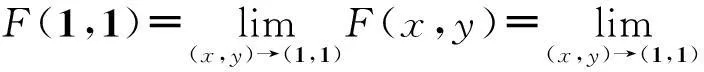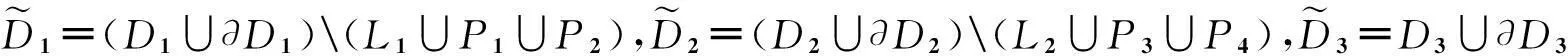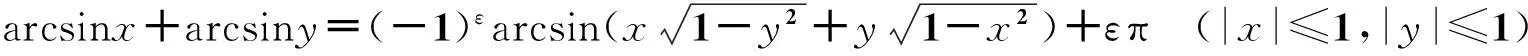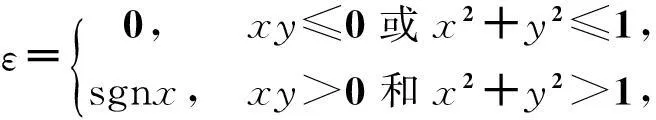利用微分方程证明反正弦加法定理

利用微分方程证明反正弦加法定理

刘春平1，刘晓平2

(1.扬州大学数学科学学院，江苏扬州225002； 2. 扬州市职业大学数学学院，江苏扬州225002)

[摘要]利用微分方程和函数的连续性给出了反正弦加法定理一种新证法，该证法可清晰地显示如何分区域讨论问题.

[关键词]微分方程； 连续性； 反正弦加法定理

[收稿日期]2014-09-15

[中图分类号]O171[文献标识码]C

1引言

反正弦加法定理是数学分析中一个经典的定理，吉米多维奇数学分析习题集[1]第777题为

证明反正弦加法定理

(1)

式中，若xy≤0或x2+y2≤1,ε=0; 若xy>0及x2+y2>1,ε=sgnx.

该定理常规的证明方法是令

2反正弦加法定理的新证法

首先考虑二元函数

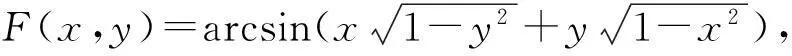
(2)

(3)

记

图1

P1=(1,0),P2=(0,1),P3=(-1,0),P4=(0,-1), 显然有L=L1∪L2. 曲线L将平面区域D分为三部分(见图1):

D1={(x,y)|x2+y2>1,0

D2={(x,y)|x2+y2>1,-1

D3=D(D1∪P1∪P2∪L1∪D2∪P3∪P4∪L2).

(i) 当(x,y)∈D1时，

因为

所以

(4)

将(4)式两边关于x积分得

F(x,y)=-arcsinx+φ1(y).

(5)

再由(5)式两边关于y求导,得

(6)

(6)式两边关于y积分得φ1(y)=-arcsiny+C1,其中C1为积分常数.因此，

F(x,y)=-arcsinx-arcsiny+C1.

(7)

(ii) 当(x,y)∈D2时，类似于(i)的推导过程，有

F(x,y)=-arcsinx-arcsiny+C2,

(8)

其中C2为积分常数.

(9)

将(9)式两边关于x积分得

F(x,y)=arcsinx+φ3(y).

(10)

再由

(11)

两边关于y积分得φ3(y)=arcsiny+C3,其中C3为积分常数.因此，

F(x,y)=arcsinx+arcsiny+C3.

(12)

由(i)～(iii)，有

(13)

下面，利用函数的连续性来确定积分常数Ck,(k=1,2,3).以∂D,∂Dk(k=1,2,3)分别表示D和Dk(k=1,2,3)的边界，注意到函数F(x,y)是初等函数，它在D∪∂D上连续，由

以及F(0,0)=arcsin0=0,arcsin0=0,可知C3=0. 此外，注意到

可知F(x,y)在L1∪P1∪P2上连续，类似可知F(x,y)在L2∪P3∪P4上连续.

综合上面结果可知

(14)

其中

3结论

[参考文献]

[1]吉米多维奇. 数学分析习题集[M]. 北京:人民教育出版社，1978: 82.

[2]费定晖，周学圣，等.吉米多维奇数学分析习题集题解1 [M]. 4版. 济南: 山东科学技术出版社，2014，196-197.

Using Differential Equation Prove the Arcsine Addition Theorem

LIUChun-ping1，LIUXiao-ping2

(1. Institute of Mathematics, Yangzhou University, Yangzhou Jiangsu 225002, China;

2. Institute of Mathematics, Yangzhou Polytechnic College, Yangzhou Jiangsu 225002, China)

Abstract:By using differential equation and continuity of function, a new proof of the arcsine addition theorem is given. This method can clearly show how to partition domains and discuss the problem.

Key words: differential equation; continuity； arcsine addition theorem