关于无穷Riemann积分与Lebesgue积分的关系及其应用的若干注记
姚 磊,姚云飞,王先超,武忠文
(1.阜阳师范学院 经济学院,安徽 阜阳 236037;2.中央财经大学 金融学院,北京 100081;3.阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
关于无穷Riemann积分与Lebesgue积分的关系及其应用的若干注记
姚 磊1,2,姚云飞3*,王先超3,武忠文3
(1.阜阳师范学院 经济学院,安徽 阜阳 236037;2.中央财经大学 金融学院,北京 100081;3.阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
现行的有关实变函数的文基本上只论述正常的Riemann积分和Lebesgue积分的关系,广义Riemann积分和Lebesgue积分的关系很少涉及。事实上,可以借助Lebesgue积分的理论与方法对广义Riemann积分有关问题的处理是非常有效的,而且往往互补。因此本文将研究无穷Riemann积分和Lebesgue积分的关系及其应用的有关问题,并且在Lebesgue积分的框架之下给出了一些疑难的Riemann积分的简捷的处理。
无穷;Riemann积分;Lebesgue;收敛
现行的有关实变函数的文献[1-3]基本上只论述正常的Riemann积分和Lebesgue积分的关系,非正常的Riemann积分和Lebesgue积分的关系很少涉及。事实上,可以借助Lebesgue积分的理论与方法对非正常Riemann积分有关问题的处理是非常有效的,而且往往互补。因此本文将研究无穷Riemann积分和Lebesgue积分的相互关系,给出在复杂积分计算、复杂极限、级数等问题中的应用,并且在Lebesgue积分的框架之下给出了一些疑难的Riemann积分的简捷的处理。
1 预备知识
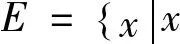
引理2[1]设f∈B[a,b],若f∈R[a,b],
则(1)f∈M[a,b]
(2)f∈L[a,b],且
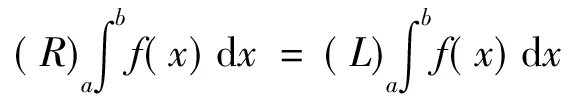
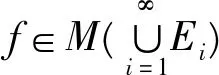
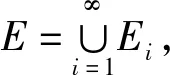
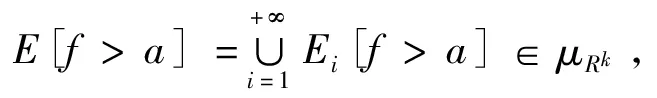
于是据[1]中的P77-78的定义知
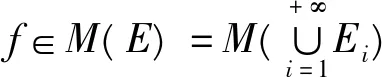
证毕。
注特别当Ei=φ,i≥n+1,i∈N时,
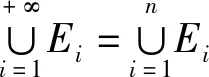
有
由此便获得[1]中的P79-80的定理3的结果。可见[1]中的P79-80的定理3为此处引理3的特例。
引理4[4]设b≠0,则 反常积分
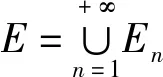
(2)f∈M+(En),n∈N+,
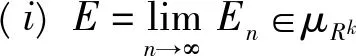
(ii)f∈M+(E),
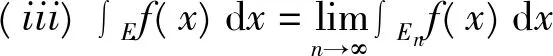
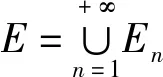
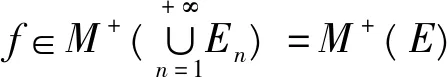
(iii)由En⊂En+1⊂E(n∈N+)知
χEn(x)≤χEn+1(x)≤χE(x),x∈E。
由f∈M+(E)知
f(x)χEn(x)≤f(x)χEn+1(x)≤f(x)χE(x),
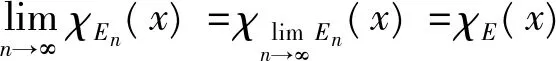
所以,由Levi定理知
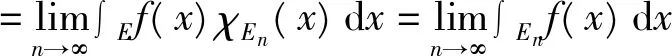
证毕。
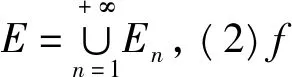
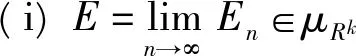
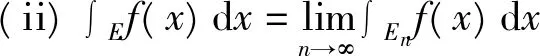
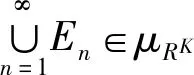
(ii)由f在E的L积分确定和引理5知
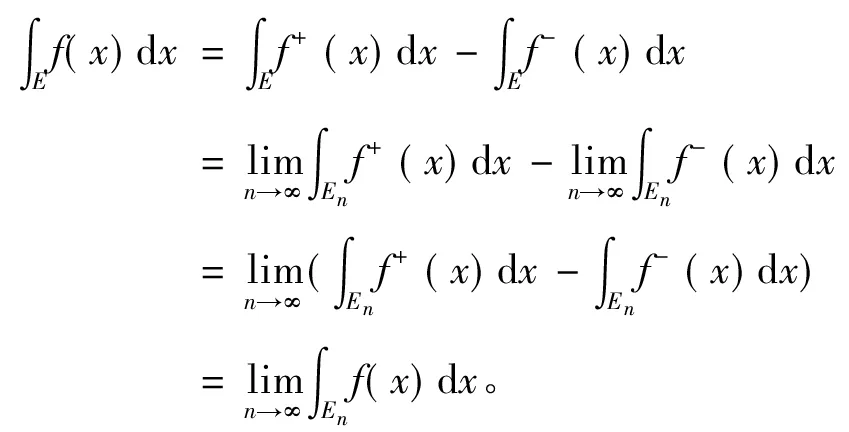
引理7[1](Levi定理级数形式) 设un∈M+(E),n∈N+,则
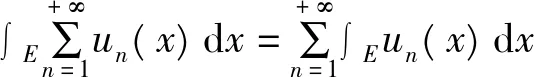
有了这些引理,它们之间某种关系将联系起来,下面请看二者的关系及其应用。
2 无穷Riemann积分和Lebesgue积分的相互关系及其应用
2.1 关系
定理1设f∈[a,+∞)→R,且∀[α,β]⊂[a,+∞),f∈R[α,β]。 若f(x)≥0,x∈[a,+∞), 则
(i)f∈M+[a,+∞),
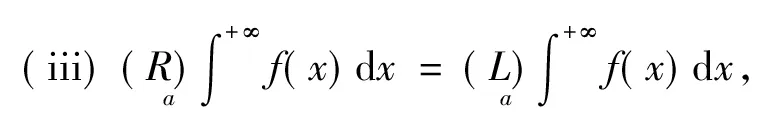
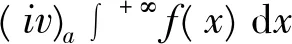
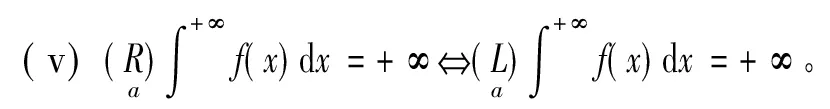
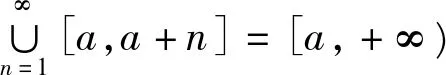
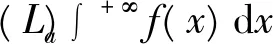
(iii) 由(ii),于是据引理5、引理2、[4]中P272-273的定义1知
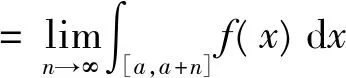
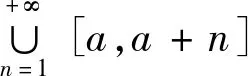
据此知(vi),(v)均成立。
证毕。
注此处定理1的提法与证法较优于[1]中的P122的定理3
定理2设f∈[a,+∞)→R,且∀[α,β]⊂[a,+∞),f∈R[α,β],则
(i)f∈M[a,+∞),

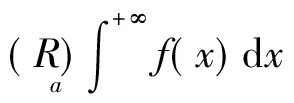
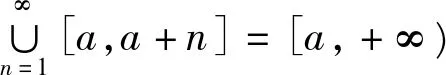
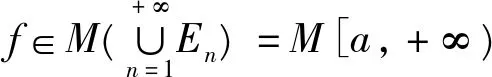
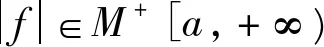
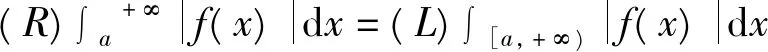
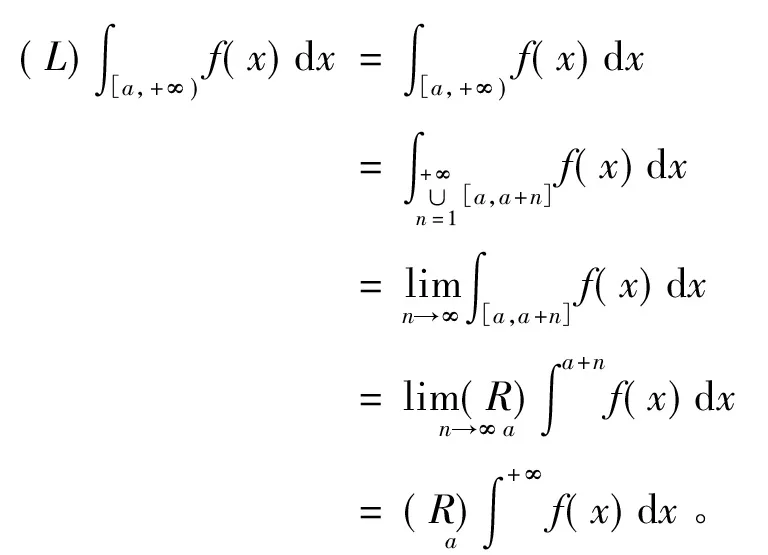
所以(iii)、(iv)成立。
证毕。
定理3设f:(-∞,a]→R,且∀[α,β]⊂(-∞,a],f∈R[α,β]。 若f(x)≥0,x∈(-∞,a] 则(i)f∈M+(-∞,a],
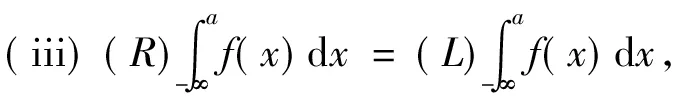

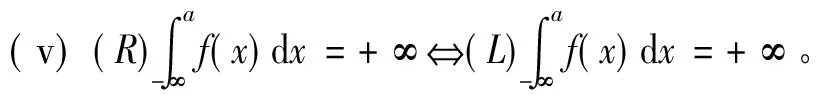
证法同定理1。
定理4设f:(-∞,a]→R,且∀[α,β]⊂(-∞,a],f∈R[α,β],则
(i)f∈M(-∞,a],
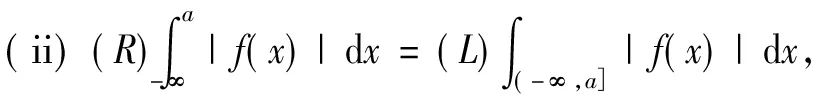
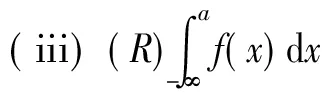
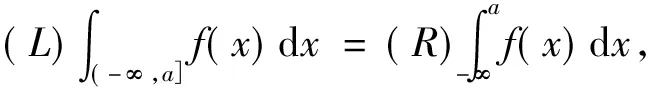
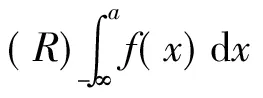
证法同定理2。
定理5设f:(-∞,+∞)→R,且∀[α,β]⊂(-∞,+∞),f∈R[α,β]。 若f(x)≥0,
x∈(-∞,+∞) 则
(i)f∈M+(-∞,+∞),
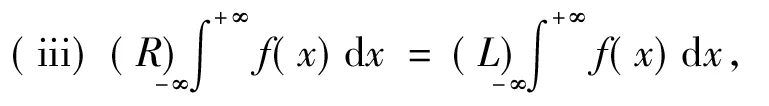

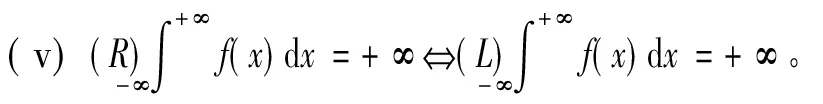
证法同定理1。
定理6设f:(-∞,+∞)→R,且∀[α,β]⊂(-∞,+∞),f∈R[α,β]则
(i)f∈M(-∞,+∞),
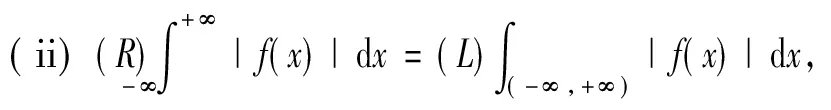
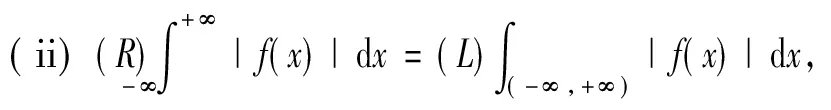
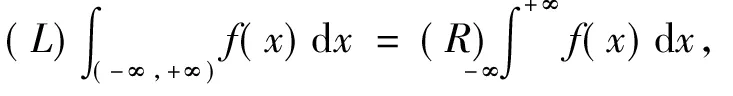
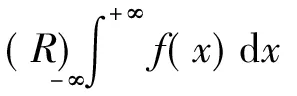
证法同定理2。
注(1)可以讨论R的瑕积分与L的积分的关系。(2)结合上述的结果可以讨论无穷积分中被积函数含有有限个的瑕点的情形。
研究了这些无穷R积分与L积分的关系,那么这些关系都特别有用。下面我们将研究它们的应用。
2.2 应用
2.2.1 计算复杂的积分
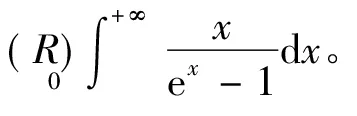
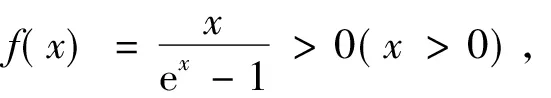
据定理1(iii)知
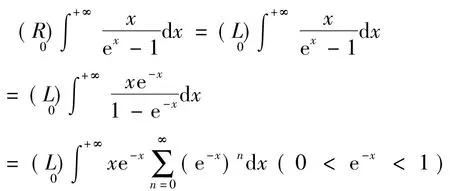
(据[5]中的P23例2)

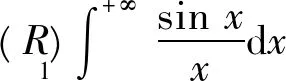
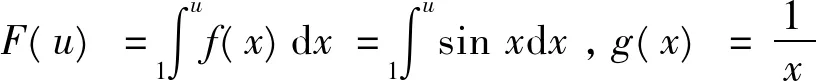
据[4]中的P280定理11.3(Dirichlet判别法)知对于∀u≥1,
|F(u)|=|cos u-cos 1|≤2,
g(x)当x→+∞时单调趋于0。故
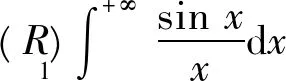
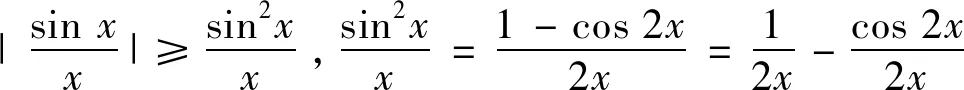
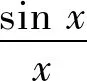
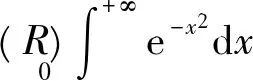


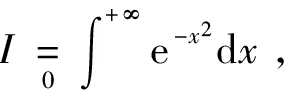
又据[1]中的P130的定理4(即Fubini定理)知
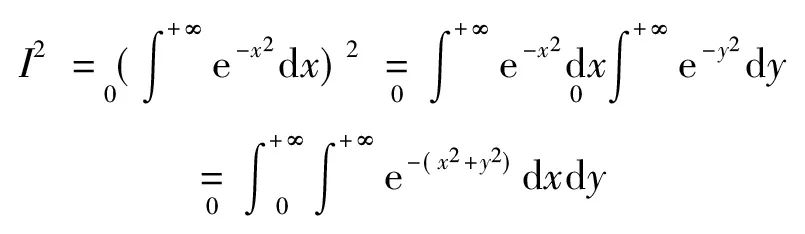
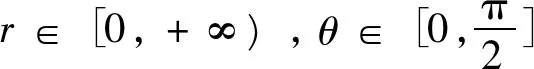
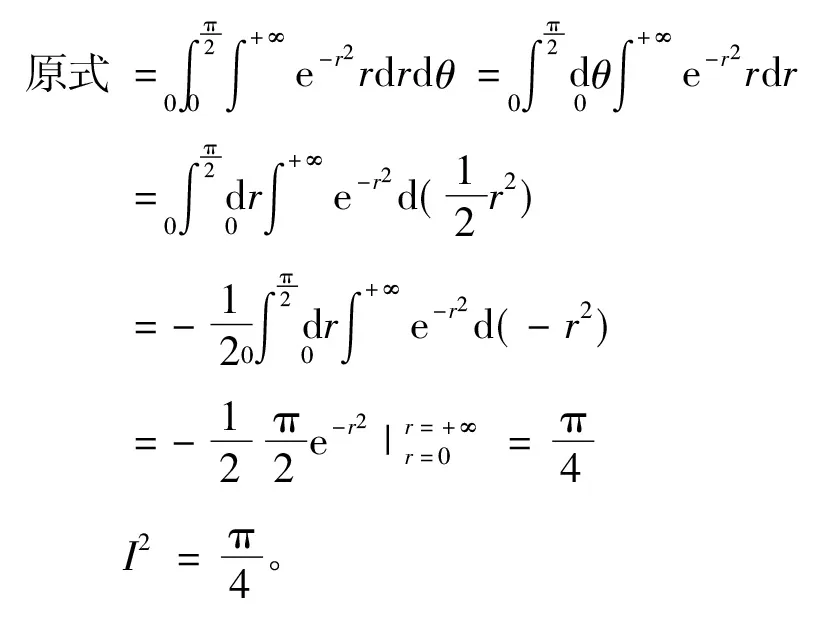
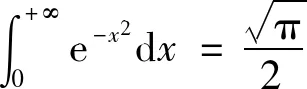
例4设P0⊂[0,1]是Cantor集,令
试求 ∫[0,1]f(x)dx的值
解由题设知f(x)≥0,x∈E,(其中E=[0,1]),E=(E-P0)∪P0,m(P0)=0,
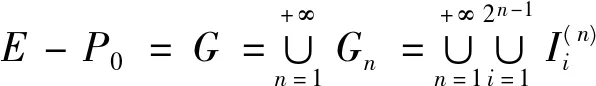
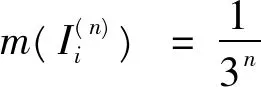
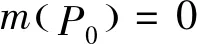
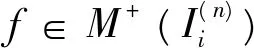
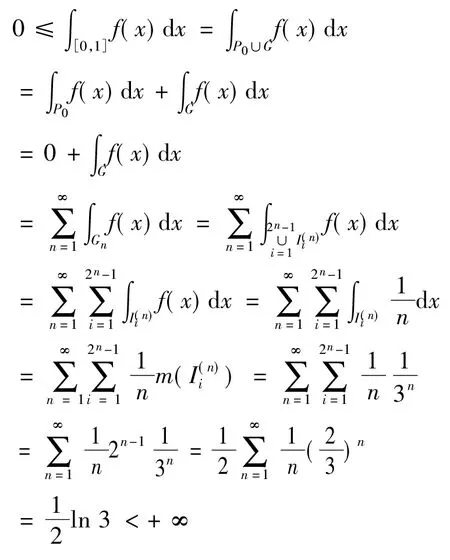
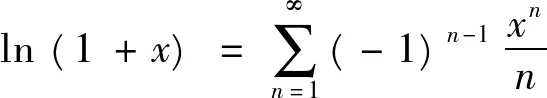
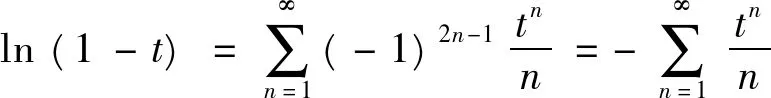
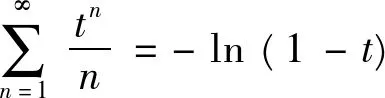
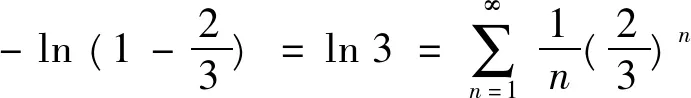
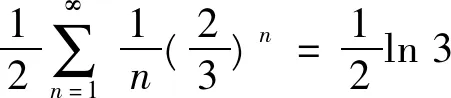
例5设p>0,b>a,
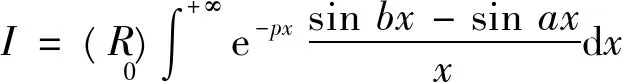
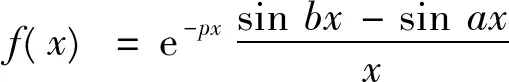
则 由 f(x)之状且据[4]中的P132-133的定理6.8(洛必达法则)知
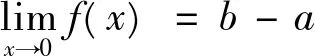
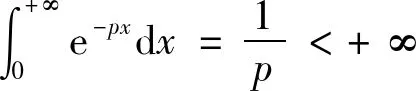
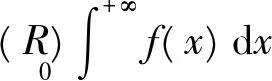
于是由定理2(iii)与[1]中的P130的定理4(即Fubini定理)知
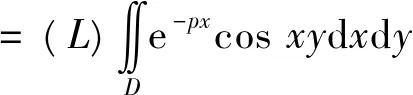
其中D=[0,+∞)×[a,b],
g(x,y)=e-pxcosxy∈M(D),
|g(x,y)|=|e-pxcosxy|≤e-px,(x,y)∈D
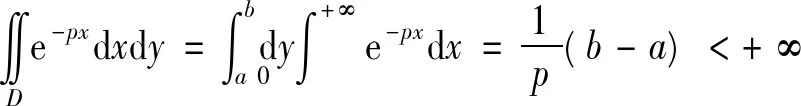
所以g∈L(D),于是由定理2(iii)与[1]中的P130的定理4(即Fubini定理)知
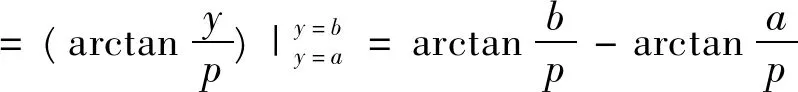
注此处较[5]中的P199例5的处理方法简单,并没有用一致收敛的有关定理和方法。因为数学分析中的一致收敛的问题是其三大一致问题之一,是比较难的。
2.2.2 求复杂的极限
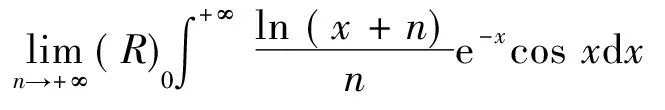
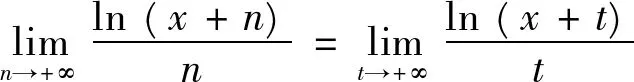
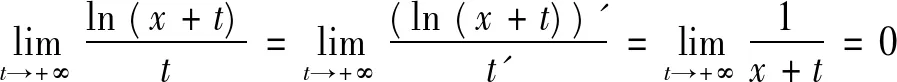
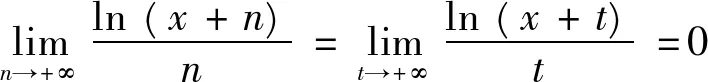
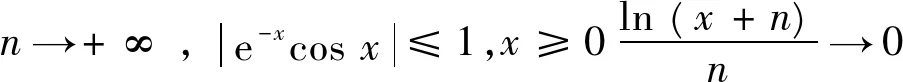
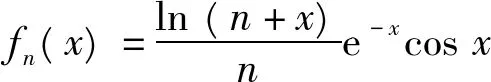
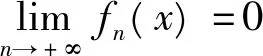
且由其状知
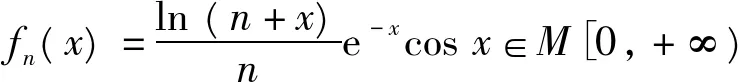
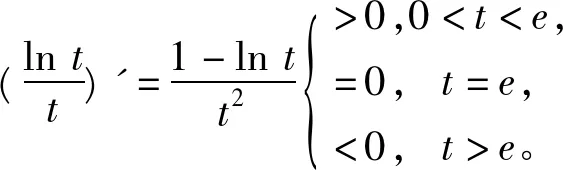
所以当n≥3,x≥0时(x+n≥3),
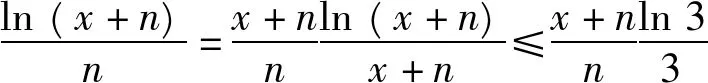
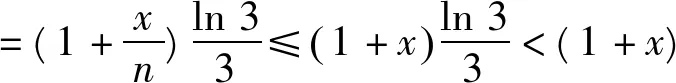
因为(1+x)e-x>0,且
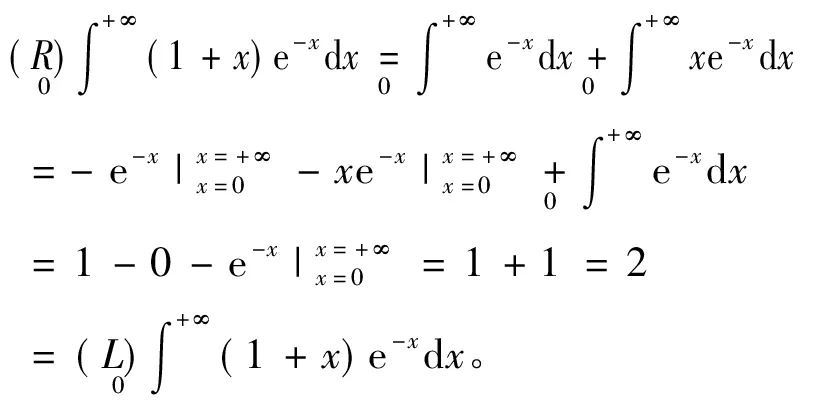
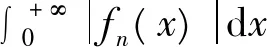
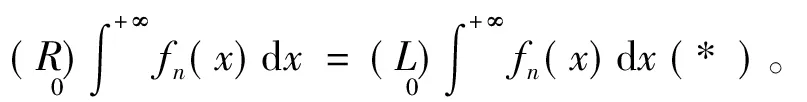
于是据[1]中的P114的定理5知
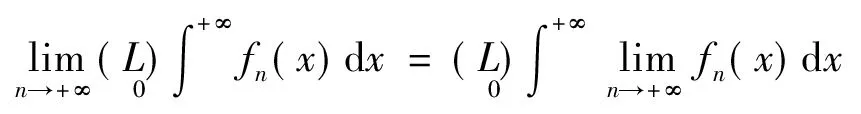
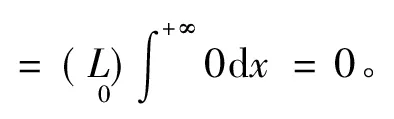
所以在(*)的两边取极限得
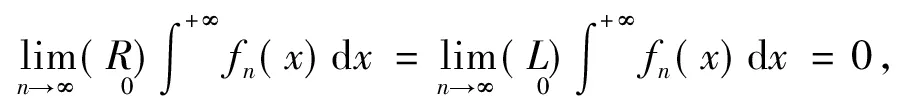
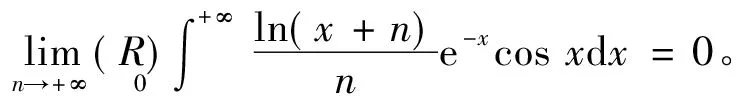
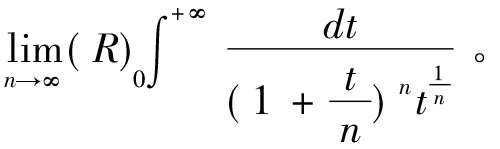
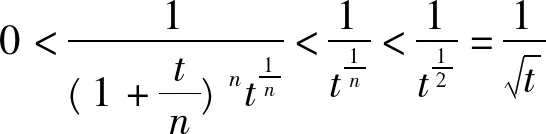
当t∈[1,+∞)时,n>2,
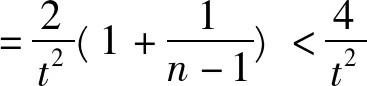
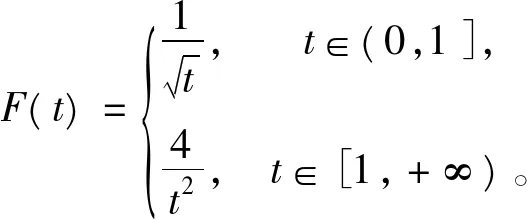
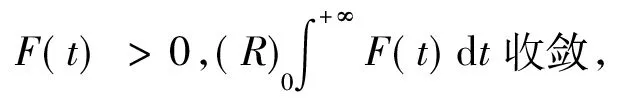
故根据引理5与[1]中的P114的定理5知
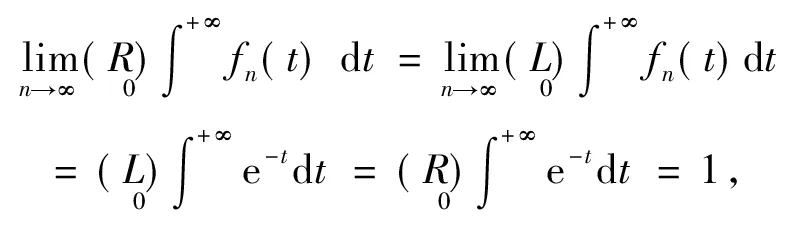
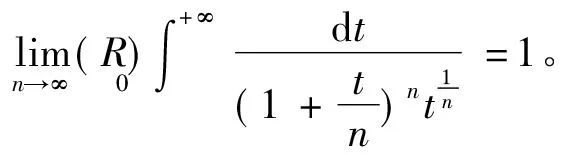
注例1、例2中没有用到数学分析中的一致收敛的定理和方法,而是用实变函数中的勒贝格控制收敛定理来解决问题,进而简化了计算。
2.2.3 级数中的应用
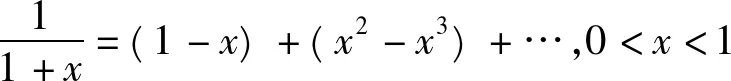
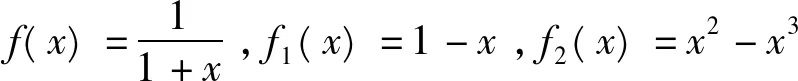
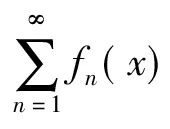
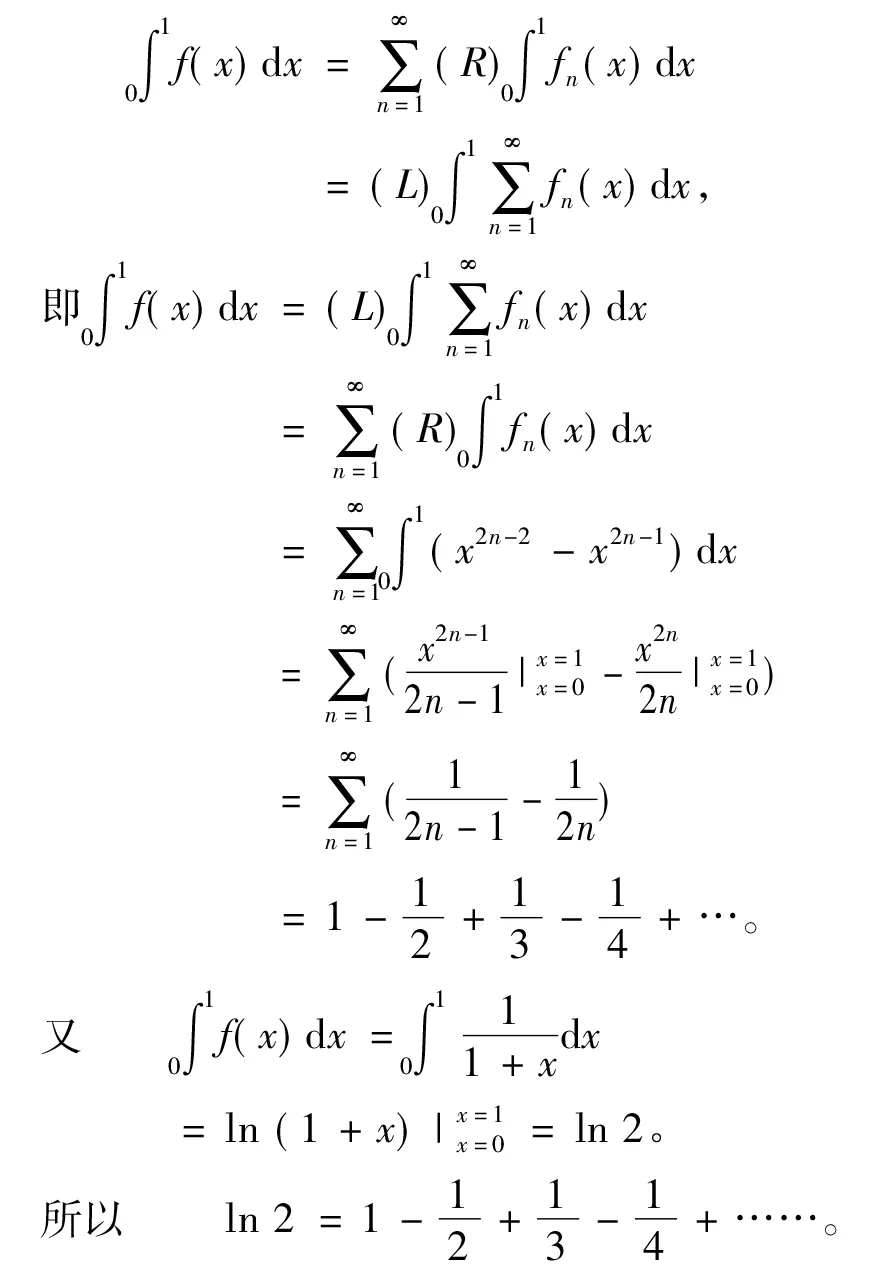
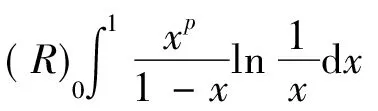
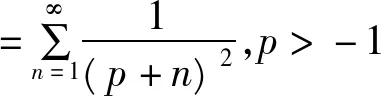
证明由定理1知
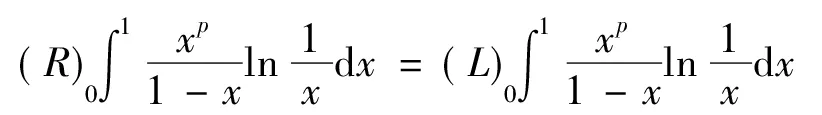
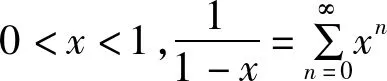
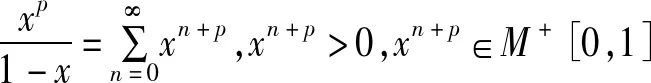
故由引理7知
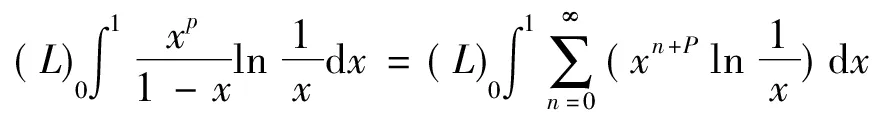
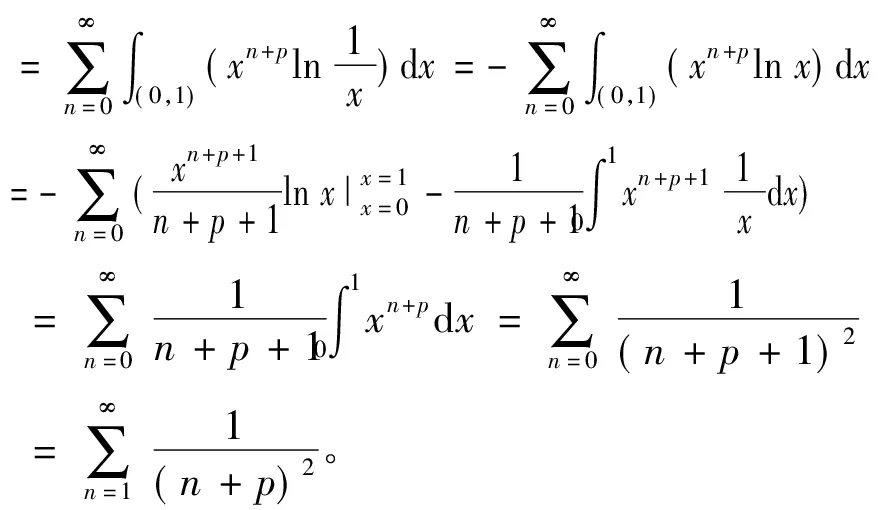
注此问题题中没有用函数项级数的一致收敛性,而是通过Levi定理的级数形式将函数的积分号与求和符号互换,从而简便计算。
3 结束语
依据Lebesgue积分与Riemann积分的特性知在k维欧式空间Rk中,当k≥2,k∈N 时,Lebesgue积分完全涵盖了Riemann积分。但在k=1时,就不一定。
[1] 程其襄,张奠宙,魏国强,等.实变函数与泛函分析基础[M].3版.北京:高等教育出版社,2012:121-122.
[2] 周民强.实变函数论[M].2版.北京:北京大学出版社,2008.
[3] 刘培德.实变函数教程[M].北京:科学出版社,2006:101.
[4] 华东师范大学数学系.数学分析(上)[M].4版.北京: 高等教育出版社,2010:54,132-133,272-273,280,287.
[5] 华东师范大学数学系.数学分析(下)[M].4版.北京:高等教育出版社,2010:23,77,89,199.
[6] Jones F. Lebesgue integration onEuclidean space[M]. massachusetts: jones and bartlett publishers, 2010: 206-207.
[7] Polga G,Sego G. Problems and Theorems in Analysis[M].Springer-Verlag-Berlin,1972:143-145.
[8] 周性伟.实变函数[M].2版.北京:科学出版社,2004:78-88.
[9] 胡适耕.实变函数[M].北京:高等教育出版社, 施普林格出版社,1999:93-97.
[10]徐森林.实变函数论[M].合肥:中国科学技术大学出版社,2002:284-290.
[11]胡适耕.姚云飞,数学分析:定理.问题.方法[M].北京:科学出版社,2007:151-152.
Some notes on relationship between infinite integral of Riemann and Lebesgue integral and its application
YAO Lei1,2,YAO Yun-fei3*,WANG Xian-chao3,WU Zhong-wen3
(1.School of Economics, Fuyang Normal University, Fuyang Anhui 236037, China;2.School of Finance, Central University of Finance and Economics, Beijing 100081, China;3.School of Mathematics and Statistics, Fuyang Normal University, Fuyang Anhui 236037, China)
The existing literature on real variable function basically discusses the relationship between normal Riemann integral and Lebesgue integral, while the relationship between abnormal Riemann integral and Lebesgue integral rarely involved. In fact, with the help of the theory and method of Lebesgue integral, abnormal Riemann integral issues related to treatment is very effective, and often complements each other. So this article will study the infinite range of Riemann integral and Lebesgue integral relationship and its application, and under the framework of Lebesgue integral, some simple processing of Riemann integral difficulty are given.
infinite;Riemann integral; Lebesgue integral; convergence
2015-08-15
国家特色专业(TS11496);全国统计科学计划项目(2011LY094);阜阳师范学院重点学科(2010XK-03)资助。
姚 磊(1982-),女,博士研究生,讲师,研究方向:金融学、金融数学。
姚云飞(1956-)男,教授,研究方向:随机泛函分析、供应链与优化、凸分析、模式识别。Email:yaoyunfeiyry@126.com。
O17,O174.1
A
1004-4329(2015)04-017-08
10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-017-08

