时域电磁反演的五种共轭梯度算法对比研究

刘广东

(阜阳师范学院 物理与电子工程学院，安徽 阜阳 236037)

时域电磁反演的五种共轭梯度算法对比研究

刘广东

(阜阳师范学院 物理与电子工程学院，安徽 阜阳 236037)

挑选梯度算法是时域电磁反演过程的重要步骤之一，选择是否恰当直接关系到反演性能。本文精选了PRP、FR、DY、HS、LS等五种常用的共轭梯度算法，共同处理两个典型的一维问题，分别反演光滑型、非光滑型的电参数(相对介电常数和电导率)分布。仿真结果的对比表明，PRP共轭梯度法的总体性能最优。

电磁反演；共轭梯度算法；时域；有限差分法

时域电磁反演方法是指通过已知的入射电磁波辐照感兴趣的散射目标，根据测得的时域散射波，直接在时域反演散射目标电磁参数的空间分布[1]。该方法已广泛应用在遥感、地球物理、无损检测、生物医学工程等领域[2-5]。为了克服电磁反演问题的非线性困难，通常将该问题转化为最小化问题迭代求解[4, 5]。

确定性算法和现代随机(进化)算法是当前解算最小化问题的两大类主要算法。其中，确定性算法主要包含最速下降法、共轭梯度(conjugategradient,CG)法、牛顿法、拟牛顿法等[6]。其中，共轭梯度法由于具有收敛快、存储量小、实现复杂度低等突出优点，提出至今不仅获得了广泛应用，而且有了一系列新发展，已经提出了多种共轭梯度算法，主要有PRP(Polak-Ribière-Polyak)共轭梯度法、FR(Fletcher-Reeves)共轭梯度法、DY(Dai-Yuan)共轭梯度法、HS(Hesteness-Stiefel)共轭梯度法、LS(Liu-Storey)共轭梯度法等[6, 7]。

然而，研究也显示：求解同样的问题，不同共轭梯度算法的性能也一般不同[7]。那么，处理时域电磁反演问题，究竟该选取哪一种共轭梯度算法最佳？为此，本文通过两个一维问题算例，对比研究前述5种共轭梯度算法的反演性能，以期为选择时提供依据。

1 问题描述

假设条件：假定问题所涉及的媒质均是各向同性、线性、无磁、无色散。

首先，将时域电磁反演问题表示为约束最小化问题：(1)其目标泛函F为[8, 9]

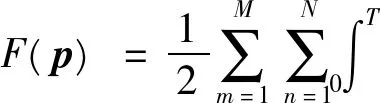
(1)

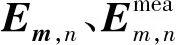
▽×Em+μ0∂tHm=0

(2a)

(2b)

其次，引入分别对应于Em、Hm的拉格朗日(Lagrange)矢量乘子em、hm，将前述约束最小化问题转化为无约束最小化问题[5]，其增广目标泛函Fa为

(3)

然后，类似于文献[5]，通过变分计算，易得重建区r处Fa关于p各分量的Fréchet导数(梯度)分别为

(4a)

(4b)

其中，δ为一阶变分算子[5]；同时，Lagrange矢量乘子em、hm满足下列方程组

▽×em-μ0∂thm=0

(5a)

(5b)

可见，方程组(2)和(5)具有相似的形式，本文采用时域有限差分(finite-differencetime-domain,FDTD)法求解[10]。

2 问题求解

预定义梯度列向量为g=: [gε,gσ]T，这样，有了梯度的解析表达，只要利用已有的共轭梯度(CG)算法迭代求解：记第k步迭代的反演参数为pk，则下一步迭代的更新公式为[6, 7]

pk+1=pk+αkdk

(6)

其中，k= 1, 2, ...,K，K为迭代总步数，αk、dk分别是第k步迭代的步长、方向向量，前者通过求解一维线搜索问题获得[6]，后者通过求解下式[6, 7]

(7)

得到，其中βk是标量因子，由于其计算公式的不同，产生了不同的共轭梯度算法，其中PRP、FR、DY、HS、LS共轭梯度法的标量因子分别为[6, 7]

(8)

时域电磁反演的技术流程基本相似，具体的流程图参阅文献[5]。

3 结果和分析

为了对比研究不同共轭梯度算法的反演性能，并考虑篇幅所限，选择处理类似于文献[4]的一维反演问题，其几何模型如图1所示：厚度为4d的重建区占据分层目标媒质；两侧毗邻厚度d= 10mm的均匀背景媒质(其电参数假定先验知晓，相对介电常数、电导率分别为εr= 5.0、σ= 0.02S·m-1)，每侧各放置1个发射、接收天线(建模为点)，分别距离重建区d/2、d/4；外接10层完美匹配层(perfectlymatchedlayer,PML)吸收边界[10]。

图1 一维反演问题几何模型

发射天线的激励源采用如下的超宽带(ultra-wideband,UWB)脉冲平面波源：

(9)

其中t0= 0.09m/c0，td= 0.03m/c0，c0为真空光速。FDTD离散化的空间、时间步长分别取为Δz= 0.5mm、Δt= 0.5Δz/c0，入射波的辐照时间T= 600Δt，以迭代总步数K= 20为迭代终止判据，迭代过程的均方根误差(meansquareerror,MSE)参见文献[1]的定义。

为不失一般性，下文给出同时反演相对介电常数εr和电导率σ的两个算例，分别处理光滑型、非光滑型分布，迭代初值均取自背景媒质(分别如图2～5中虚线所示)，对比研究5种不同共轭梯度算法的反演性能。

图2 光滑型分布相对介电常数的真实值、迭代初值和不同共轭梯度算法反演终值对比

算例1重建区真实的电参数呈类似正弦的光滑型分布：相对介电常数分布如图2中实线所示，其峰值、谷值分别为9.0、1.0；电导率分布如图3中实线所示，其峰值、谷值分别为0.04S·m-1、0.00S·m-1。

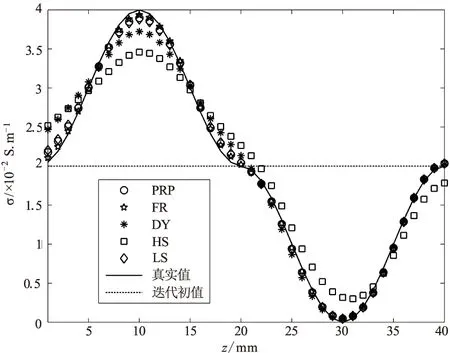
图3 光滑型分布电导率的真实值、迭代初值和不同共轭梯度算法反演终值对比

分别应用PRP、FR、DY、HS、LS五种不同的共轭梯度算法，经过20步迭代时，得到的反演结果为：相对介电常数分布分别如图2中圆、正五边形、星号、正方形、菱形所示，均方根误差对比如表1中第2行所示；电导率分布分别如图3中圆、正五边形、星号、正方形、菱形所示，均方根误差对比如表1中第3行所示。

就光滑型相对介电常数分布而言，表1、图2的结果对比表明：PRP共轭梯度法的性能相对最好；HS共轭梯度法的性能相对最差。就光滑型电导率分布而言，表1、图3的结果对比表明：FR共轭梯度法的性能相对最好；PRP共轭梯度法的性能相对较好；HS共轭梯度法的性能相对最差。

表1 光滑型分布的反演均方根误差对比

算例2重建区真实的电参数呈阶梯状的非光滑型分布：相对介电常数分布如图4中实线所示，其最大值、最小值分别为9.0、1.0；电导率分布如图5中实线所示，其最大值、最小值分别为0.04S·m-1、0.00S·m-1。

分别应用PRP、FR、DY、HS、LS五种不同的共轭梯度算法，经过20步迭代时，得到的反演结果为：相对介电常数分布分别如图4中圆、正五边形、星号、正方形、菱形所示，均方根误差对比如表2中第2行所示；电导率分布分别如图5中圆、正五边形、星号、正方形、菱形所示，均方根误差对比如表2中第3行所示。

图4 非光滑型分布相对介电常数的真实值、迭代初值和不同共轭梯度算法反演终值对比

就非光滑型相对介电常数分布而言，表2、图4的结果对比表明：PRP共轭梯度法的性能相对最好；HS共轭梯度法的性能相对最差。就非光滑型电导率分布而言，表1、图3的结果对比表明：PRP共轭梯度法的性能相对最好；LS共轭梯度法的性能相对较好；HS共轭梯度法的性能相对最差。

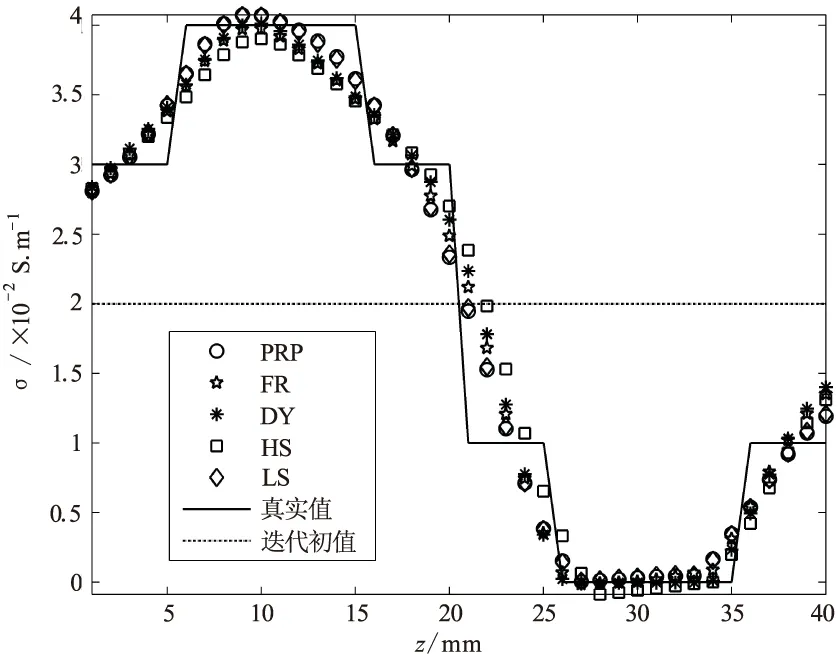
图5 非光滑型分布电导率的真实值、迭代初值和不同共轭梯度算法反演终值对比

表2 非光滑型分布的反演均方根误差对比

对比同型(光滑型或非光滑型)分布的不同参数时发现，相对介电常数的反演误差大于电导率的反演误差，这表明在所用的激励源频谱中，高频分量占优，相对介电常数对散射场的贡献大[1]；对比不同类型分布的相同参数(相对介电常数或电导率)时发现，非光滑型的反演误差大于光滑型的反演误差，这表明非光滑型加剧了逆问题的病态特性[1]；适当增加迭代次数，或尝试引入适当的正则化技术[1, 5]，有望进一步减小误差。

综合以上两个算例的结果得出：利用5种不同的共轭梯度算法同时反演(光滑型或非光滑型)的电参数(相对介电常数和电导率)分布，PRP共轭梯度法的总体性能最优。

4 结语

时域同时反演目标媒质的介电常数和电导率是常用的电磁反演方法之一，在无损检测、目标识别等领域具有良好的应用价值。而选择梯度算法是其重要环节之一，直接影响反演质量甚至反演成败。为此，本文选择5种常用的共轭梯度算法，反演了(光滑型、非光滑型)两个一维算例的电参数(相对介电常数、电导率)分布，仿真结果的对比显示，PRP共轭梯度算法的总体性能最优。

[1] 刘广东，张开银．二维电磁逆散射问题的时域高斯-牛顿反演算法[J]．物理学报，2014，63(3)：116-130．

[2] 翁爱华，李大俊，李亚彬，等．数据类型对三维地面可控源电磁勘探效果的影响[J]．地球物理学报，2015，58(2)：697-708．

[3]ZhangJ,YangK,TongMS.Inversionofscatteringdataforreconstructingdielectricobjectswithlimitedobservationangles[J].IEEEAntennasandWirelessPropagationLetters, 2014, 13(1): 83-86.

[4]PapadopoulosTG,RekanosIT.Time-Domainmicrowaveimagingofinhomogeneousdebyedispersivescatterers[J].IEEETransactionsonAntennasandPropagation, 2012, 60(2): 1197-1202.

[5] 刘广东，张业荣．早期乳腺癌检测的二维时域微波断层成像方法[J]．阜阳师范学院学报(自然科学版)，2010，27(3)：3-9．

[6] 马昌凤．最优化方法及其Matlab程序设计[M]．北京：科学出版社，2010：1-75．

[7]DaiYH.Afamilyofhybridconjugategradientmethodsforunconstrainedoptimization[J].MathematicsofComputation, 2003, 17(2): 1317-1328.

[8]PapadopoulosTG,RekanosIT.EstimationoftheparametersofLorentzdispersivemediausingatime-domaininversescatteringtechnique[J].IEEETransactionsonMagnetics, 2012, 48(2): 219-222.

[9]MoriyamaT,TakenakaT.Inversescatteringapproachwithmeasurementofonlytotalelectricfield[J].MicrowaveandOpticalTechnologyLetters, 2015, 57(1): 137-141.

[10]葛德彪，闫玉波．电磁波时域有限差分法[M]．3版．西安：西安电子科技大学出版社，2011：9-96．

The comparative research on five conjugate gradient algorithms for time-domain electromagnetic inversion problems

LIU Guang-dong

(SchoolofPhysicsandElectronicEngineering,FuyangNormalUniversity,FuyangAnhui236037,China)

Selectingonefrommanyconjugategradient(CG)algorithmsisoneimportantstepforsolvingtime-domainelectromagnetic(EM)inversionproblems,therefore,whetheritisappropriateornotisdirectlyrelatedtopropertiesoftheinversion.Inthispaper,fiveCGalgorithms,namelyPRP(Polak-Ribière-Polyak),FR(Fletcher-Reeves),DY(Dai-Yuan),HS(Hesteness-Stiefel)andLS(Liu-Storey),areselectedtosimultaneouslyreconstructthespatialdistributionoftheelectricalpermittivityandelectricconductivityfromtwotypicalone-dimensional(1-D)problems,forsmoothtypeandroughtype,respectively.ComparisonofthesimulatedresultsindicatesthatthepropertyfromthePRPCGalgorithmisthebestone.

electromagnetic(EM)inversion;conjugategradient(CG)algorithms;timedomain;finitedifferencemethod

2015-04-01

国家自然科学基金(51271059)；安徽省科技计划项目(1501031114)；安徽高校省级自然科学研究重点项目(KJ2014A193)；阜阳师范学院自然科学基金(2014FSKJ14)资助。

刘广东(1972-)，男，博士，副教授，研究方向：电磁反演理论。

O441.4

1004-4329(2015)04-029-05

10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-029-05