导数概念的教学探究

王志刚，姚 艳，董书一

(1. 阜阳师范学院 数学与统计学院，安徽 阜阳 236037；2. 阜阳城郊中学，安徽 阜阳 236000；3.蚌埠三十一中，安徽 蚌埠 233000)

导数概念的教学探究

王志刚1，姚 艳2，董书一3

(1. 阜阳师范学院 数学与统计学院，安徽 阜阳 236037；2. 阜阳城郊中学，安徽 阜阳 236000；3.蚌埠三十一中，安徽 蚌埠 233000)

导数是高等数学的核心概念之一，在自然科学，工程技术和经济管理等最优化问题中有着非常广泛的应用。导数的概念具有较强的抽象性和严密的逻辑性，许多学生都未能掌握其思想和本质。为了帮助学生理解导数，在课堂教学中可先结合具有专业背景的实例和微积分发展史，引出导数的概念，激发学生的学习兴趣；再通过极限理论，完成导数概念的感性认识到理性认识的升华；最后，挖掘导数蕴含的哲学思想，培养大学生的辩证唯物主义观。

导数；极限；平均变化率；瞬时变化率

高等数学是理学类、工程类和经济类等专业的一门必修的基础课，不仅是该专业许多后继课程的重要工具，而且还影响着学生将来的发展。导数是高等数学的核心概念之一，是研究函数性质的重要工具，在自然科学，工程技术和经济管理等最优化问题中有着非常广泛的应用。导数概念具有较强的抽象性和严密的逻辑性，给教师的教学和学生的学习带来了一定的困难[1-4]。为了帮助学生理解导数的概念，在课堂教学中可先结合具有专业背景的实例和微积分发展史，引出导数的概念，激发学生的学习兴趣；再通过极限理论，让学生完成导数概念的感性认识到理性认识的升华；最后，挖掘导数蕴含的哲学思想，培养大学生的辩证唯物主义观。

1 导数概念的引入

自2003年新课程改革以后，“导数及其应用”成为高中数学的教学内容。为了突出导数概念的思想和本质，新课标要求高中的导数教学不再强调极限的概念，而利用“逼近的思想”，通过物理上的运动问题和几何上的切线问题，让学生经历由平均变化率到瞬时变化率刻画现实问题的过程，理解导数概念，体会导数的思想及其内涵，并掌握导数在函数单调性和极值求解等方面的应用。因此，高中生对导数的概念已具有了感性的认识。为了从感性认识升华到理性认识，大学教师在导数的概念教学中，可结合专业问题背景和微积分发展历程，引导学生深入探究导数概念的内涵和外延，真正地理解导数概念的思想和本质。

1.1 结合专业问题,引出导数的概念

由于学生已经学习了导数的概念，并对“已知路程求速度”，“已知曲线求切线”等问题都有了一定的了解。如果再按这种思路引出导数的概念，既显示不出高校教师的教学水平，也会影响学生学习的积极性，让学生产生“已理解导数概念”的错觉。为了激发大学生学习高等数学的积极性，我们应通过一些与学生所学专业相关的实例，引出导数的概念。例如：电子类专业，可使用电的传输中电流强度的变化率；化工类专业，可使用化学反应中溶液的浓度变化率；经济类专业，可使用弹性函数，边际成本等问题。这些实际问题最终都归结为“求函数平均变化率的极限”，从而得到导数的定义：

(1)

其中Δy=f(x0+Δx)-f(x0)。另外，(1)式也可以表示成

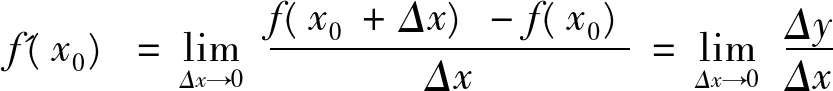
1.2 通过微积分发展史，激发学生的兴趣

导数是函数平均变化率的极限，极限是导数概念的基础。但是，在牛顿和莱布尼茨创立微积分时，他们并没有利用极限来定义导数，导致了导数概念的混淆不清，最终引发了第二次数学危机。例如，计算f(x)=x2的导数，按照牛顿的“流数术”，令Δx为x处的非零增量，Δy为Δx引起的函数增量，即Δy=f(x+Δx)-f(x)=(x+Δx)2-x2=2x·Δx-Δx2,

则

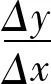
2 导数概念的升华

根据高等数学教材的编排，在导数学习之前，学生已经深入地学习了数列极限、函数极限和函数的连续性，对极限概念已经有了一定的认识，已经利用极限理论研究了函数的连续性和连续函数的性质，也对极限的学习产生了比较高的积极性，为导数概念的学习奠定了良好的基础。因此，在导数概念引入之后，可引导学生利用极限理论探讨导数的存在性。提出问题： 什么函数一定可导？如何求函数的导数？

2.1 可导的必要条件

回顾无穷小的性质，并引导学生观察(1)式的极限。归纳、总结出(1)式极限存在的充分必要条件是：

当x→x0时，f(x)-f(x0)是x-x0的同阶或高阶无穷小量。

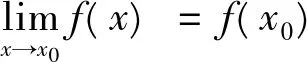
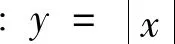
2.2 可导的充要条件

类比左右极限的定义，引出左导数

(2)

和右导数

(3)

再借助数列收敛与子列收敛的关系的思想，让学生总结出f(x)在x0处可导的充要条件是：f(x)在x0处的左右导数存在且相等。

2.3 可导的等价形式

在以往的教学和学习过程中发现，虽然学生记住了(2)的形式，但没有真正理解它的含义，经常会产生一些疑惑。通过例1，让学生真正理解(1)式的内涵和外延，让学生对导数的概念达到深度的理解。

例1下面的哪种形式和定义1的(1)式等价。

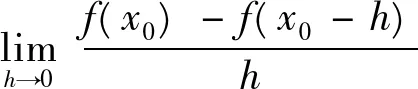
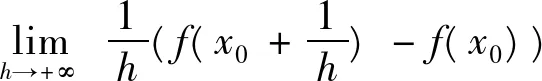
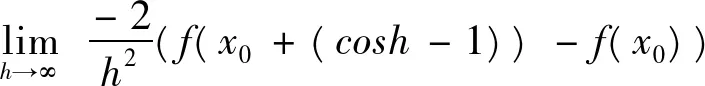
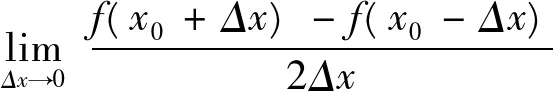
注解：A,B,C同属于增量广义化的问题，即

(4)

提醒学生要注意：极限中的三个“□”必须“一模一样”，并且，既可以□→0+，又可以□→0-，才可以与(2)式等价。A是正确的，B和(4)式等价，C和(3)式等价。而D的问题在于，改变了极限定义式中的一静一动组合，不再包含f(x0)的任何信息，也是错误的。例如函数

3 导数概念的哲学思想

教书育人是教师的天职，也是教师的基本使命和主要工作。数学和哲学又有着密切的联系。因此，在高等数学课堂里，我们不仅要向学生传授数学知识，而且要充分利用数学中的哲学思想，培养学生的辩证唯物主义观[6]。

否定之否定揭示了事物的矛盾运动过程，由自我否定向对立面转化的过程。从导数的几何意义看，为了求曲线y=f(x)在点A(x0,f(x0))处的切线，在曲线上再取一点B(x0+Δx,f(x0+Δx))，其中Δx≠0。直线AB是曲线的割线，并不是过A点的切线。当Δx减小，直线AB开始转动，并向A点的切线逐步逼近。如果Δx→0，直线AB就会趋向于A点的切线。当Δx≠0时，割线不可能是切线，是对切线的否定；当Δx→0时，直线AB的极限不可能是割线，是对割线的否定。因此割线到切线的转变过程就是否定之否定的过程。在生活中，我们也应学会使用“否定之否定”的哲学思想处理问题，从事物的对立面出发，进行分析和思考，从而找到解决问题的方案。

综上所述，高等数学中导数概念的教学，应突出极限的基础地位，注重培养学生利用极限去研究导数的概念，借助问题驱动法，激发学生的探究意识，实现导数概念的感性认识到理性认识的升华。同时，我们也应该挖掘导数概念中蕴含的辩证法的思想，进一步培养大学生的辩证唯物主义观。

[1] 王雅萍．浅谈导数概念的教学策略[J]．通化师范学院学报，2013，34(10)：81-82．

[2] 王淑芝．导数教学对学生素质教育的培养[J]．吉林省教育学院学报，2009，25(9)：70-71．

[3] 郑 莲．关于导数概念的几个典型错误解析[J]．成都师范学院学报，2013，29(3)：123-124．

[4] 孙亚仙．论高职学院数学的分层教学[J]．湖南师范大学教育科学学报，2008，7(2)：127-128．

[5] 同济大学应用数学系．高等数学[M]．北京：高等教育出版社，2003．

[6] 王志刚，姚云飞．“最值定理”的教学探究[J]．阜阳师范学院学报(自然科学版)，2014，31(1)：79-81．

Teachingresearchontheconceptofderivative

WANGZhi-gang1,YAOYan2，DONGShu-yi3

(1.SchoolofMathematicsandStatistics,FuyangNormalUniversity,FuyangAnhui236037; 2.TheMiddleSchoolofChengjiao,FuyangAnhui236000,China；3.No.31MiddleSchool,BengbuAnhui233000,China)

Theconceptofderivativeisoneofthemostimportantconceptsinadvancedmathematics,andhasaverywiderangeofapplicationsinnaturalscience,engineeringtechnologyandeconomicmanagement.Becauseitisvery

andlogicalsothatmanystudentscannotunderstandthisconcept.Inordertoovercomethedifficulty,wefirstlyintroducethederivativebyexamplesofprofessionalbackgroundandthehistoryofcalculus,secondlyusethelimittheorytoobtaintheconditionofderivative,lastlyexplorephilosophythoughtofthederivativetocultivateundergraduate'sdialecticmaterialisticviewpoint.

derivative；limit；averagerateofchange；instantaneousrateofchange

2015-05-25

安徽省质量工程项目(2013zy167，2015jxtd121，2014zy138)；阜阳师范学院质量工程(2013jyxm22, 2013jyxm34，2014JXTD01，2013ZYSD05)；阜阳师范学院"国培计划"项目(FYGP1402)资助。

王志刚(1979-)，男，博士，副教授，研究方向：非线性偏微分方程。

O172.1

A

1004-4329(2015)04-105-03

10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-105-03