傅立叶变换性质在瞬时频率构造中的应用

韦永梅，赵发勇

(阜阳师范学院 物理与电子工程学院，安徽 阜阳 236037)

傅立叶变换性质在瞬时频率构造中的应用

韦永梅，赵发勇

(阜阳师范学院 物理与电子工程学院，安徽 阜阳 236037)

利用傅立叶变换的性质研究信号希尔伯特变换的频谱特征。在频域内一个因果信号的频谱实部与虚部互为变换。一个信号和它的变换式能构成一个解析信号，解析信号的实部就是原信号，其虚部是原信号的希尔伯特变换；解析信号的傅立叶频谱只有正频率部分，正好是原信号正频率部分的二倍，并且该解析信号的幅值和相位就表征了原信号的幅值包络和瞬时频率变化特征，这样就使瞬时频率瞬时幅值有了明确的物理意义，对研究非线性非稳态信号有非常重要的价值。

希尔伯特变换；因果信号；解析信号；瞬时频率

瞬时信号的特征提取对于分析非平稳非线性信号具有十分重要的意义。随着现代技术发展,要准确地识别研究信号内部特征，就要求高精度提取信号的瞬时参数。然而复杂信号真正意义上的瞬时参数定义比较困难,更谈不上高精度测量信号的瞬时参数。变换可以巧妙地应用解析表达式中的实部与虚部的正弦和余弦关系,定义出任意时刻的瞬时频率、瞬时相位及瞬时幅度,从而解决了复杂信号中的瞬时参数的定义及计算问题,使得对于时间有限信号和复杂多分量信号的瞬时参数的提取成为可能，所以它在信号处理中有着极其重要的作用[1]。即使有些复杂信号不满足变换的条件,可以经过分解,然后进行变换,达到提取信号瞬时特征的目的。在工程中如何实现变换对信号的瞬时特征提取,特别如何提取瞬时频率特征及提高信号特征精度等问题很有研究价值。

在信号与系统分析中,系统可实现性的实质是具有因果性，不仅时限信号、无时限信号经常用因果信号来表示,而且在实际中获得的信号大多是因果信号。利用傅立叶变换的性质可以推出因果信号的傅里叶变换的实部与虚部互不独,它们之间可通过变换形式表示出相互制约特性。一个信号和它的变换式能构成一个解析信号，解析信号的实部就是原信号，其虚部是原信号的希尔伯特变换；利用傅立叶变换的性质推出了解析信号的傅立叶频谱只有正频率部分，而且正好是原信号的正频率部分的二倍，解析信号和原实信号自身本质是一致的。研究解析信号的频谱特点就能得到原信号正频率部分的频谱特征。并且利用Hilbert变换和解析信号的特征可以得到原实信号的任意时刻的模和相位变化特征，该解析信号的幅值和相位就表征了原信号的幅值包络和瞬时频率变化特征，可以实现对原实信号的瞬时特征提取，定义出任意时刻的瞬时频率、瞬时相位和瞬时幅值等重要的瞬时参量[2-3]，这样就使瞬时频率瞬时幅值有了明确的物理意义，对研究非线性非稳态信号有非常重要的价值。

2 Hilbert变换的频域特征及其在信号分析中的应用

2.1Hilbert变换的定义

把某一实函数f(x)的希氏变换记为H[f(t)]，则有：

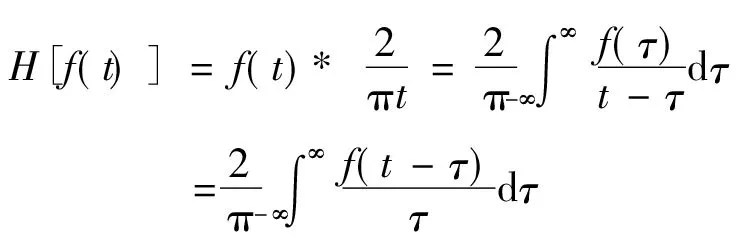
(1)

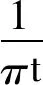
2.2 利用傅立叶变换对称和卷积性质分析Hilbert变换的频谱

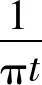
(2)

由傅立叶变换的对称性质得：

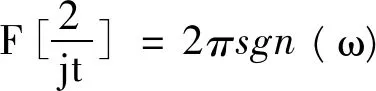
由此得：

(3)

即Hilbert变换的冲激响应h(t)的傅立叶变换是-jsgn (ω)。即：

(4)

由上式得知，Hilbert变换在频域内了完成对信号的移相。

由傅立叶变换的卷积性质，得到信号f(t)经Hilbert变换后的频谱为：

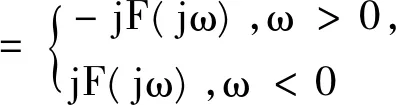
(5)

从一些常用信号的Hilbert变换结果也可以反映这个特点，例如

H[cosωt]=sinωt，

H[sinωt]=-cosωt，

H[a(t)cosωt]=a(t)sinωt。

同理，利用傅立叶变换可以推导出一个信号经过两次希尔伯特变换后的频谱为：

=F(jω)·[-jsgn(ω)]·[-jsgn(ω)]

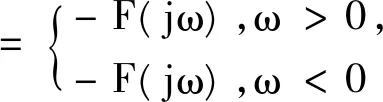
(6)

由此得知一个信号经过两次Hilbert变换后在频域内就是一个理想的移相器，信号经过Hilbert变换相当于对信号的正频率部分移相180度，对负频率部分移相180度。

2.3 利用傅立叶变换卷积性质分析Hilbert与因果信号的关系

在信号与系统分析中,系统可实现性的实质是具有因果性，不仅时限信号、无时限信号经常用因果信号来表示,而且在实际中获得的信号大多是因果信号。

设x(t)是实因果信号，当t<0时，x(t)=0。则x(t)=f(t)·u(t)，利用傅立叶变换的卷积性质得到x(t)的傅立叶变换为：

=Re[X(jω)]+Im [X(jω)]

(7)

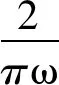
2.4 利用傅立叶变换的奇偶性和线性分析Hilbert变换与解析信号的关系

设信号x(t)为一个实信号,利用x(t)及其希尔伯特变换H[x(t)]构造一个复信号z(t)：

z(t)=x(t)+jH[x(t)]=atejθ(t)

=a(t)cosθ(t)+ja(t)sinθ(t)

(8)

称z(t)为x(t)的解析信号，其中a(t)为解析信号的模，θ(t)为相角。

已知实信号x(t)的频谱设为Re(ω)+jIm(ω),由傅立叶变换定义式我们能推出其实部对ω是偶对称的,虚部对ω是奇对称的,即:

(9)

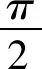
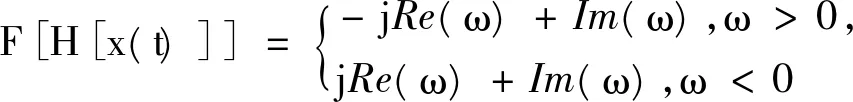
(10)

将H[x(t)]再移相，即乘以j,得jH[x(t)]的频谱为：

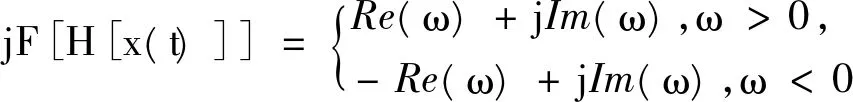
(11)

利用x(t)及其希尔伯特变换H[x(t)]构造一个复信号z(t)：

z(t)=x(t)+jH[x(t)]=a(t)ejθ(t)=a(t)cosθ(t)+ja(t)sinθ(t)，称z(t)为的x(t)解析信号，其中a(t)为解析信号的模，θ(t)为相角。该解析信号的频谱为：

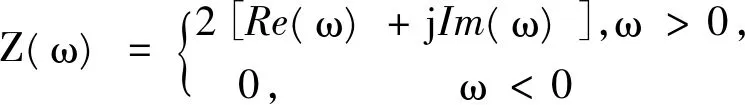
(12)

在实信号分析中,利用构建解析信号的方法,可以得到一个实信号x(t)在复空间的映射z(t)为原信号x(t)的解析信号。从这个复空间映射中得知实部与虚部互为Hilbert变换,由Hilbert变换的90度相移功能,可以推断,解析信号的实部与虚部是互相正交的。解析信号z(t)的幅值为a(t)，相位为θ(t)，两者皆为时间函数，而且a(t)也正好是原信号的幅度包络，θ(t)也正好是原信号x(t)的瞬时相位。

另外，由解析信号的频谱的傅立叶反变换也可以推出解析信号与原信号的重要关系。由解析信号的频谱Z(ω)和原信号的频谱X(jω)关系：

(13)

其中U(ω)是频域内单位阶跃信号。已知阶跃信号u(t)的傅立叶频谱为：

(14)

由傅立叶变换的对称性质得：

(15)

由此推导出解析信号的傅立叶反变换为：

z(t)=F-1[Z(ω)]=F-1[2X(jω)U(ω)]

(16)

由上式可知解析信号z(t)的实部正好是原信号x(t)，虚部也正是原信号x(t)的希尔伯特变换。解析信号和原实信号自身本质是一致的。解析信号的实部就是原信号，其虚部是原信号的希尔伯特变换；而且利用傅立叶变换的性质推出了解析信号z(t)的傅立叶频谱只有正频率部分，而且正好是原信号x(t)的正频率部分的二倍，研究解析信号的频谱特点就能得到原信号正频率部分的频谱特征。

2.5 Hilbert变换与瞬时频率的关系

利用x(t)及其希尔伯特变换H[x(t)]构造一个复信号z(t)：

z(t)=x(t)+fH[x(t)]=a(t)ejθ(t)=a(t)cosθ(t)+ja(t)sinθ(t)。

幅值为a(t)，相位为θ(t)，两者皆为时间函数，而且a(t)也正好是原信号的幅度包络，θ(t)也正好是原信号X(t)的瞬时相位。由Hilbert变换定义式可以看出HT就是实现信号X(t)和1/t的卷积，积分结果仍是时间的函数，所以从时间分布可能得出实部信号X(t)的局部时间特性。从构造的解析信号的极坐标表示中也反映了信号X(t)的局部时间特性，因为其幅度及相位均是时间的函数。

因此，利用Hilbert变换和解析信号的特征可以得到原实信号的任意时刻的模和相位变化特征，可以实现对原实信号的瞬时特征提取，定义出任意时刻的瞬时频率、瞬时相位和瞬时幅值等重要的瞬时参量。这样瞬时角频率定义为解析信号相位的导数[7]:

(17)

从上式定义的瞬时频率可以看出，瞬时频率ω(t)是t的单值对应函数，即有一个时间点就有与之相对应的一个频率值。用解析信号的相位的导数来定义瞬时频率是比较合理的。对于多分量信号，在某个时刻就有多个频率成份，这时就没有清楚的瞬时频率概念。据此，得出只有一个单分量信号的频率成分才对应有瞬时频率意义。在Huang等人提出HHT之前,人们很早就提出了瞬时频率概念和信号的多分量结构。许多学者也试图在此基础上继续对瞬时频率进行研究,并作了大量的工作,但这些工作都没有先给出单分量信号的合理定义。如果直接对信号进行Hilbert变换，在任意时刻只能得到唯一的瞬时频率，这与多分量信号的多频率成份意义不一致。为了获得真正有意义的瞬时频率必须加一定的限制条件才可以。

实际信号存在许多非窄带信号，且许多信号存在局部出现频率波动很大的情况，同一信号可能有多个频率成份，对这样的信号直接进行希尔伯特变换，就失去原有的物理意义。为此，希尔伯特-黄变换定义了单分量信号即固有模态函数概念，并提出经验模态分解方法对信号进行分解，用经验筛分法将信号先分解成单分量信号，这样可以不直接对信号作希特尔伯特变换，而是分解后对每个分解的分量进行希尔伯特变换然后利用解析信号的特点，定义瞬时频率，对每个分量分别计算瞬时频率。从而解决了复杂信号中的瞬时参数的定义及计算问题,使得对于时间有限信号和复杂多分量信号的瞬时参数的提取成为可能，所以它在信号处理中有着极其重要的作用。

3 结论

利用傅立叶变换及其性质研究希尔伯特变换频谱特征，一个实因果信号的傅立叶变换的虚部通过希尔伯特变换被实部唯一确定，反过来也一样。一个信号和它的变换式能构成一个解析信号，解析信号的实部就是原信号，其虚部是原信号的希尔伯特变换。变换可以巧妙地应用解析表达式中的实部与虚部的正弦和余弦关系,定义出任意时刻的瞬时频率、瞬时相位及瞬时幅度,从而解决了复杂信号中的瞬时参数的定义及计算问题,使得对于时间有限信号和复杂多分量信号的瞬时参数的提取成为可能，所以它在信号处理中有着极其重要的作用。

[1] 刘慧婷，程家兴，张 旻．利用Hilbert变换提取信号瞬时特征的算法实现[J]．微机发展，2003，13(6)：82-85．

[2] 孙艳争．EMD时频分析理论与应用研究[Z]，2007．

[3] 钟佑明，金 涛，秦树人．希尔伯特-黄变换中的一种新包络线算法[J]．数据采集与处理，2005，20(1)：13-17．

[4] 陈 君，崔祥霞，肖 静，等．基于径向希尔伯特变换的图像边缘增强特性研究[J]．光子学报，2011(3)：483-486．

[5] 侯瑞宁．希尔伯特变换在同轴数字全息再现中的应用[J]．激光技术，2013(3)：362-364．

[6] 王 珂，肖鹏峰，冯学智，等．基于改进二维离散希尔伯特变换的图像边缘检测方法[J]．测绘学报，2012，41(3)：421-427, 433．

[7] 李风民．希尔伯特变换及其应用研究[J]．中国无线电，2006(7)：53-54．

TheapplicationofthepropertiesofFouriertransformininstantaneousfrequencystructure

WEIYong-mei，ZHAOFa-yong

(SchoolofPhysicsandElectronicEngineering,FuyangAnhui236037,China)

ThispaperstudiesspectrumcharacteristicsoftheHilberttransformationbythepropertiesoftheFouriertransformation.Infrequencydomain，realpartandimaginarypartofacausalsignalspectrumaretheHilberttransformationeachother.AsignalanditsHilberttransformcanconstituteaanalyticalsignal,therealpartoftheanalyticalsignalistheoriginalsignal,theimaginarypartistheHilberttransformationoftheoriginalsignal;TheFourierspectrumofanalyticalsignalcontainsonlythepositivefrequencypart,whichisjusttwotimesoftheoriginalsignal,andtheanalyticsignalamplitudeandphasewillrepresenttheoriginalsignalamplitudeenvelopeandinstantaneousfrequencyvariationcharacteristics,sotheinstantaneousfrequencyandinstantaneousamplitudehaveclearphysicalmeaning,whichisveryimportanttostudynonlinearunsteadysignal.

Hilberttransformation;causalsignal;analyticsignal;instantaneousfrequency

2015-10-15

基于北斗定位及物联网技术的农情监测系统研发与示范(1501031114)；阜阳师范学院质量工程项目(2013ZYSD05)资助。

韦永梅(1971-)，女，硕士，讲师，研究方向：信号处理。

TN-9

A

1004-4329(2015)04-045-04

10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-045-04