三阶正交矩阵的性质及其应用

黄 瑞，刘剑桥，周俊东

(阜阳师范学院 a.数学与统计学院；b.外国语学院， 安徽 阜阳 236037)

三阶正交矩阵的性质及其应用

黄 瑞a，刘剑桥b，周俊东a

(阜阳师范学院 a.数学与统计学院；b.外国语学院， 安徽 阜阳 236037)

本文利用矩阵的相关知识和拉格朗日恒等式证明了三阶正交矩阵的一个性质，并由此给出曲线曲率、挠率、曲面的三个基本形式、高斯曲率和平均曲率等在合同变换下的变化规律。

正交矩阵；合同变换；曲率；挠率；曲面的三个基本形式

1 三阶正交矩阵的一个性质及其证明

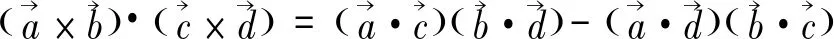
证明根据混合积的定义和向量的二重向量积的计算法则得

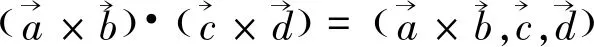
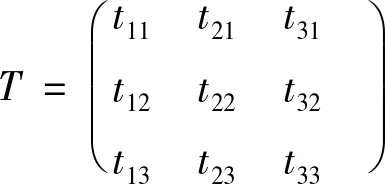
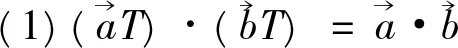
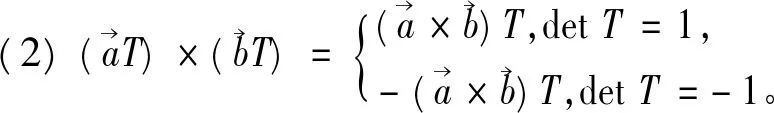
证明(1)首先将正交矩阵T进行分块

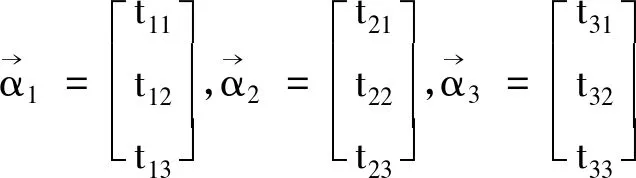
根据正交矩阵的定义

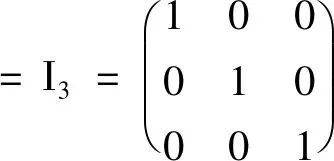
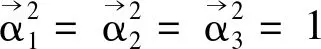
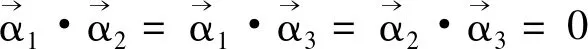
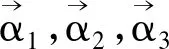
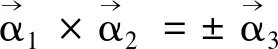
又det(TΤT)=detTΤdetT=(detT)2=1,即detT=±1，

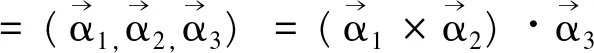
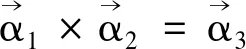
根据矩阵乘法有

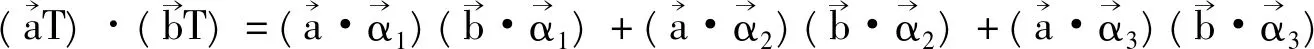
当det T=1时,

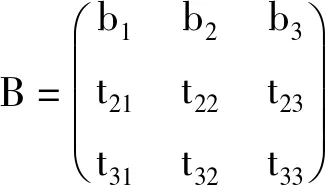
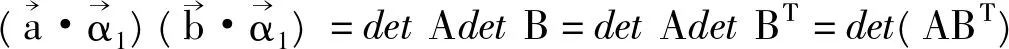
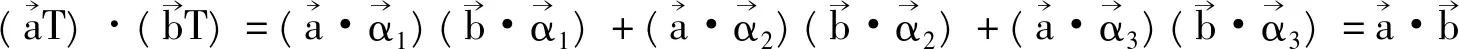
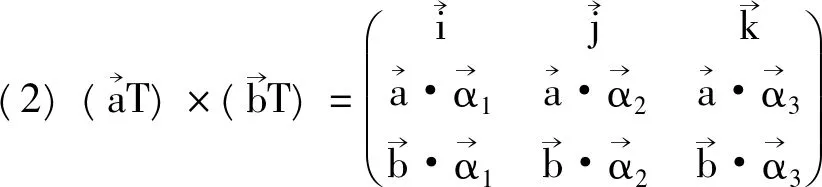
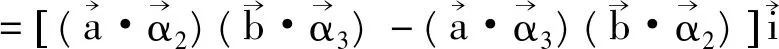
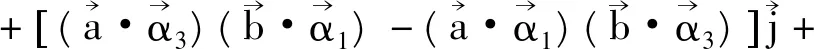
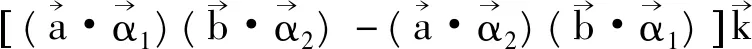
根据Lagrange恒等式有

det T=1时, 有

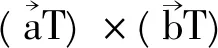
det T=-1时, 有

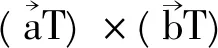
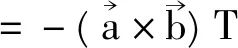
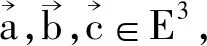
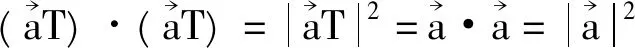
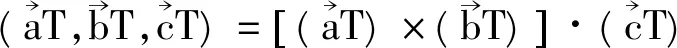
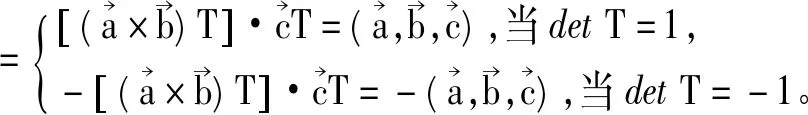
2 性质1在微分几何中的应用

曲率和挠率是空间曲线的两个重要几何量，在不考虑空间位置的情况下，这两个几何量完全决定了空间曲线的形状。[2,3]对曲率和挠率进行了研究。曲面的第一、第二、第三基本形式是研究曲面的最基本的工具， [4-7]给出了这方面的研究。[8]仅研究了刚体运用对曲线和曲面的一些量的影响。本文用新的方法研究了曲线的曲率、挠率以及曲面的第一、第二、第三基本量等几何量在合同变换下的变化规律。

性质2[1]设Γ为E3中的合同变换，则∀X∈E3,Γ(X)=XT+P0,其中T为3阶正交矩阵，P0∈E3。

[1]用两种不同的方法给出了证明。

性质3曲线的曲率在合同变换下保持不变；挠率在刚体运动下保持不变，在反刚体运动下变为原来的相反数。

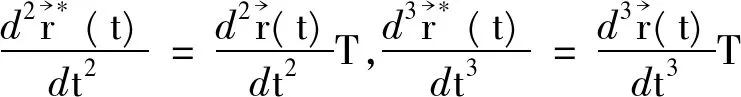
由推论1得：

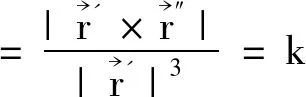
其中τ为曲线(C)的挠率。

性质4曲面的第一、第三基本量在合同变换下保持不变，第二基本量在刚体运动下保持不变，在反刚体运动下变为原来的相反数。

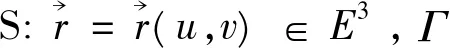
(1)

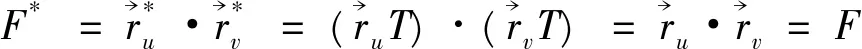
(2)

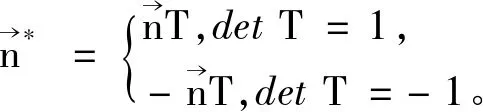
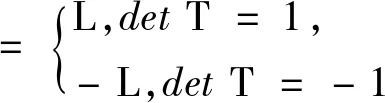
(3)

同理可得

(4)

由性质1和推论1得

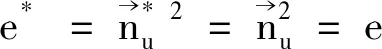
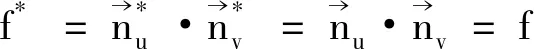
(5)

推论2曲面的第一、第三基本形式、高斯曲率在合同变换下保持不变，第二基本形式、平均曲率在刚体运动下保持不变，在反刚体运动下变为原来的相反数。

证明由(1)(2)得

Ι*=E*du2+2F*dudv+G*dv2=Edu2+2Fdudv+Gdv2=Ι。

由(3)(4)得

由(5)得

Ⅲ*=e*du2+2f*dudv+g*dv2=edu2+2fdudv+gdv2=Ⅲ。

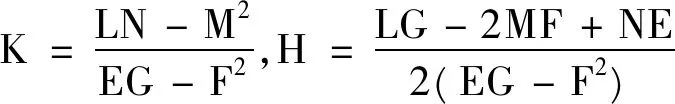
由(1)-(5)易得K=K*,

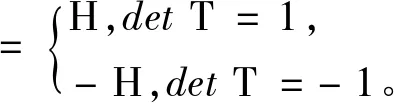
3 结束语

本文证明了三阶正交矩阵的一个性质，并给出了此性质在微分几何中的应用。根据三阶正交矩阵与合同变换之间的关系和文中的性质1及其推论1得到了曲线曲率、挠率、曲面的第一、第二、第三基本形式、高斯曲率和平均曲率在合同变换下的变化规律。另外根据合同变换与等距变换之间的关系，易知曲面的内蕴量都是在合同变换下保持不变的几何量。

[1] 彭家贵，陈 卿．微分几何[M]．北京：高等教育出版社，2002：4-10．

[2] 苏雅拉图．李志远.曲率和挠率的关系及其应用[J]．高等数学研究，2008，11(4)：16-19．

[3] 傅朝金．空间曲线的曲率和挠率[J]．高等函授学报(自然科学版)，2003，16(5)：13-14．

[4] 宋占奎．曲面的第三基本形式研讨[J]．吉林化工学院学报，2006，23(4)：79-82．

[5] 傅朝金．曲面的三个基本形式之间关系的几种证明方法[J]．高等函授学报(自然科学版)，2001，14(6)：13-14, 18．

[6] 于纯孝，王洪英．曲面的三个基本形式之间关系的注记[J]．山东师大学报(自然科学版)，1996，11(4)：10-12．

[7] 傅朝金，何汉林．曲面的三个基本形式的系数矩阵之间关系的证明及其应用[J]．海军工程大学学报，2002，24(3)：5-7．

[8] 孟令江．曲面的基本形式在欧氏变换下的固定性[J]．唐山师范学院学报，2007，29(5)：61-62．

Property of a third-order orthogonal matrices and its applications

HUANG Ruia，LIU Jian-qiaob，ZHOU Jun-donga

(a.SchoolofMathematicsandStatistics；b.SchoolofForeignLanguages,FuyangNormalUniversity,FuyangAnhui236037，China)

This paper, using related knowledge of matrices and Lagrange's identity, proves a property of a third-order orthogonal matrices, and thus provides the change law of the contract under the alteration of the curvature, torsion of a curve, three fundamental forms of a surface, the Gaussian curvature and mean curvature.

orthogonal matrices; congruent transformation; curvature; torsion; three fundamental forms of a surface

2015-07-10

国家特色专业建设项目(TS11496)；安徽省质量工程项目(2014zy138，2013jyxm553，2015jxtd121，2015gxk149)，安徽省自然科学研究项目(2014KJ002)资助。

黄 瑞(1985-)，女，硕士，讲师，研究方向：微分几何。

O186.1

A

1004-4329(2015)04-009-04

10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-009-04