求解非线性方程和方程组的安全两方计算协议
杨 侠,张 华,唐 剑
(1.阜阳师范学院 数学与统计学院,安徽 阜阳 236037;2.湖南文理学院,湖南 常德 415000)
求解非线性方程和方程组的安全两方计算协议
杨 侠1,张 华2,唐 剑1
(1.阜阳师范学院 数学与统计学院,安徽 阜阳 236037;2.湖南文理学院,湖南 常德 415000)
以不经意传输协议为基础,给出一元二次方程求解的安全两方计算协议,并以此为子协议给出一类特殊非线性方程组求解的安全两方计算协议,对协议的正确性和安全性进行说明。
不经意传输协议;一元二次方程;安全两方计算协议
安全多方计算问题是由Yao在文献[1]中首次提出,受到众多密码学家的关注,研究的重点由多方安全计算问题的一般性研究发展为针对特殊问题的研究,随后一系列的文献就具体的问题给出高效实用的安全多方计算研究[2-9]。文献[2]中讨论了半诚实模型下,基于Paillier同态加密技术的安全两方线段求交问题,给出了安全有效的协议,并把协议推广到恶意模型状态。文献[3]中利用分治策略给出集合求第k小元的安全两方计算协议。文献[4]中借助于基本的多方安全计算协议并结合Shamire秘密共享,给出一种新型匿名门限秘密共享方案。文献[5,6]中讨论理性安全多方计算问题,是博弈论和安全多方计算的综合,是一个有特色的研究方向。文献[7-9]中借助矩阵的相关协议,给出安全计算线性方程和方程组的多方安全计算协议。安全求解方程、方程组问题是安全计算问题的一个重要研究领域,而目前关于非线性方程和方程组的研究较少。文章以不经意传输协议为基础给出一元二次方程求解的安全两方计算协议,并解决了一类特殊非线性方程组的求解的安全两方计算问题。文中的数域默认为复数域。
1 预备知识
下面给出几个基本概念和基本协议。
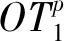
半诚实参与方:参与协议的各方都严格执行协议,在协议运行过程中不会出现中途退出或恶意加入虚假消息的行为,但允许各方记录协议中得到的数据。
文中的协议参与方都默认为是半诚实的。
协议1[10]相等检测协议。
协议2复数除法的安全两方计算协议
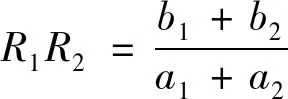
具体协议如下:
(1)Alice,Bob约定两个正整数p,m,使得pm足够大,从而pm次加法运算不可能。
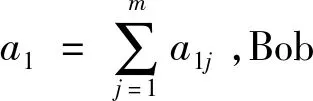
(b)Alice生成随机数h1,h2,…,hp,并发送给Bob,其中hk=a1j;
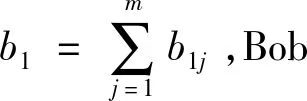
(b)Alice生成随机数u1,u2,…,up,并发送给Bob,其中ul=b1j;
(7)Alice计算
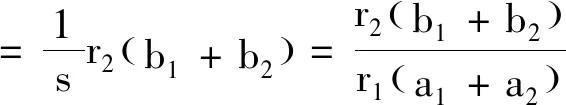
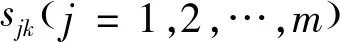
协议3[12]复数加、乘混合的安全两方计算协议。

2 主要结果
在给出关于一般一元二次方程的求解的两方安全计算协议之前先讨论下列特殊情形。
2.1 求解特殊一元二次方程
x2+a1a2x+b1b2=0
(1)
协议4 求解一元二次方程(1)的安全两方计算协议。
输入:Alice有复向量(a1,b1),Bob有复向量(a2,b2)。
输出:Alice得到数R1, Bob得到数R2,满足R1R2是方程(1)的解。
具体协议如下:
(1)Alice,Bob约定两个正整数p,m,使得pm足够大,从而pm次加法运算不可能。
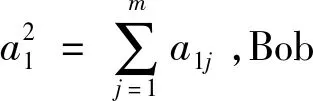
(6)当u≠0时,Alice得到R1=u。
(7)Bob生成随机数a21,a22,…,a2m,使得

(b)Bob生成随机数s1,s2,…,sp,并发送给Alice,其中sn=a2j;
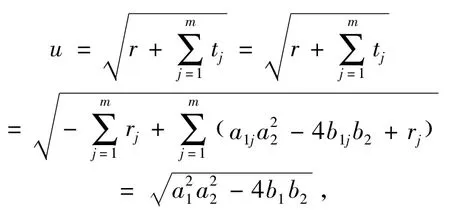

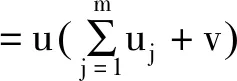
即步骤(6)-(9)正确。
2.2 求解一般复系数一元二次方程
(2)
协议5 求解一元二次方程(2)的安全两方计算协议。
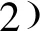
具体协议如下:
协议的正确性和保密性易得。
2.3 求解非线性方程组
(3)
以协议5为基础,讨论方程组(3)的共同求解问题。当a1+a2=0,即a1=-a2时,由协议1可以检测出来,从而为了简化协议,不妨设a1+a2≠0,同理可设mk+nk≠0.当k=1时,文献[11]中已经讨论过,从而这里不妨设k≥2。
协议6 求解复系数非齐次线性方程组(3)的安全两方计算协议。
(2)当Δ=0时,Alice,Bob执行下列子步骤:
(3)当Δ≠0时,Bob有两个不同R2,不妨设为R21,R22。Alice,Bob执行下列子步骤:
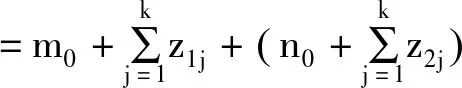
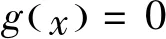
[1]YaoA.Protocolsforsecurecomputations[C]//Proceedingsofthe23rdAnnualIEEESymposiumonFoundationsofComputerScience, 1982: 160-164.
[2] 孙茂华,罗守山,辛 阳,等.安全两方线段求交协议及其在保护隐私凸包交集中的应用[J].通信学报,2013,34(1):30-42.
[3] 张永华.保护私有信息的两方求第k小元协议[J].阜阳师范学院学报(自然科学版),2014,31(2):50-53.
[4] 石润华,仲 红.一种新型匿名门限秘密共享方案[J].山东大学学报(理学版),2012,47(11):31-39.
[5]NojoumianM,StinsonDR.Socio-Rationalsecretsharingasanewdirectioninrationalcryptography[C]//andGameTheoryforSecurity, 2012: 18-37.
[6]GroceA,KatzJ.Faircomputationwithrationalplayer[C]//inCryptology-EUROCRYPT2012, 2012: 81-98.
[7]DuW,AtallahMJ.Privacy-preservingcooperativescientificcomputations[C]//ComputerSecurityFoundationsWorkshop, 2001.Proceedings. 14thIEEE.NovaScotia,Canada, 2001: 273-282.
[8] 罗文俊,李 祥.多方安全矩阵乘积协议及应用[J].计算机学报,2005,28(7):1230-1235.
[9] 贾恒越,刘焕平.求矩阵逆的安全双方计算协议[J].计算机工程与应用,2008,44(33):112-114.
[10]DuWL.Astudyofseveralspecificsecuretwo-partycomputationproblems[D].PurdueUniversity,USA, 2001.
[11]贾恒越,刘焕平.非线性方程和方程组求解的安全两方计算协议[J].计算机科学与探索,2009,3(1):98-104.
[12]李 禾,王述洋.关于除法的安全双方计算协议[J].计算机工程与应用,2010,46(6):86-88, 123.
The secure two-party protocols of nonlinear equation and nonlinear systemsof equations
YANG Xia1, ZHANG Hua2,TANG Jian1
(1. School of Mathematics Statistics, Fuyang Normal University,Fuyang Anhui 236037, China;2. Hunan University of Arts and Science, Changde Hunan 415000, China)
The secure protocol for the quadratic equation has been proposed by using Oblivious Transfer 1 out of p protocol in this paper. Then based this protocol, the secure two-party protocols for a kind system of nonlinear equationsare given. Finally, the security and correctness of the protocols has been described.
oblivious transfer protocol;quadratic equation;secure two-party protocol
2015-06-02
安徽省高校优秀青年人才基金项目(2011SQRL100);阜阳师范学院质量工程项目(2013JCJS03,2013ZYSD05)资助。
杨 侠(1978-),女,硕士,副教授,研究方向:代数及密码学。
TP309
A
1004-4329(2015)04-013-04
10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-013-04

