正规矩阵的等价刻画

刘俊同

(阜阳师范学院 数学与统计学院，安徽 阜阳 236037)

正规矩阵的等价刻画

刘俊同

(阜阳师范学院 数学与统计学院，安徽 阜阳 236037)

正规矩阵在酉相似理论中起着非常重要的作用。利用Schur定理和酉相似矩阵的特征值、奇异值、迹以及向量的内积等角度讨论了正规矩阵的若干等价条件。

正规矩阵; 酉矩阵; 上三角矩阵; 迹

正规矩阵是酉相似下保持不变的矩阵，对称矩阵，斜对称矩阵，酉矩阵以及正交矩阵都是特殊的正规矩阵，它在矩阵理论研究中起着非常重要的作用。教材[1]和[2]给出了正规矩阵的定义和几个等价条件，文献[3-6]也讨论了正规矩阵的若干等价条件。本文通过对矩阵的特征值，奇异值, 迹以及向量的内积的研究获得了正规矩阵的几个等价条件。

1 预备知识

为了叙述方便，对符号作如下约定：Cn表示复数域，Mn表示复数域上n×n矩阵的集合，A*表示A的共轭转置矩阵，tr(A)表示A的迹，Re λ表示复数λ的实部，Im λ表示复数λ的虚部。A∈Mn，A的特征值分别记为λ1,λ2,…,λn。

定义1设A∈Mn，若满足A*A=AA*，则称A是正规矩阵。

定义2设U∈Mn，若满足U*U=I，则称U是酉矩阵。

定义3设A,B∈Mn，若存在酉矩阵U，使得A=U*BU，则称A和B酉相似。

引理1 (Schur定理)设A∈Mn，A有特征值λ1,λ2,…,λn，它们按任意给定的次序排列，则存在一个酉矩阵U，使得U*AU=T=[tij]是具有对角元tii=λi,i=1,2,…,n的上三角矩阵。

引理2设A∈Mn，则矩阵A是正规矩阵当且仅当下述任一命题成立

(1)A可酉对角化，即存在一个酉矩阵U∈Mn，使得U*AU=diag(λ1,λ2,…,λn)。

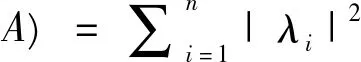
引理3设A,B∈Mn，则有(1)tr(AB)=tr(BA)；(2)tr(AA*)=0⟺A=0。

2 定理及证明

定理1设A∈Mn，则矩阵A是正规矩阵当且仅当下述任一命题成立

(a)矩阵A的奇异值分别为|λ1|,|λ2|,…,|λn|；

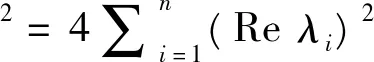
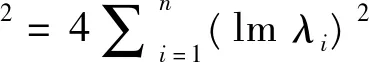
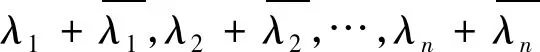
(e)tr(A*A)2=tr((A*)2A2)；

(f)(A*A)2=(A*)2A2。

证明(a)设矩阵A的奇异值分别为σ1,σ2,…,σn，于是，有

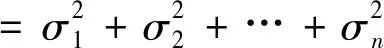
由引理2 (2)，A是正规矩阵，反之，若A是正规矩阵，由引理2 (1)，存在一个酉矩阵U∈Mn，使得U*AU=diag(λ1,λ2,…,λn)，于是，有

U*A*AU=diag((|λ1|2,|λ2|2,…,|λn|2)。

所以，矩阵A的奇异值分别为|λ1|,|λ2|,…,|λn|。

(b)不妨设A是上三角矩阵，因为由引理1，存在一个酉矩阵U，使得U*AU=T=[tij]是具有对角元tii=λi,i=1,2,…,n的上三角矩阵，于是tr(A*A)=tr(T*T)。注意到

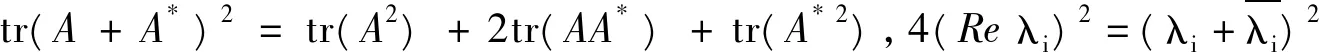
于是，有

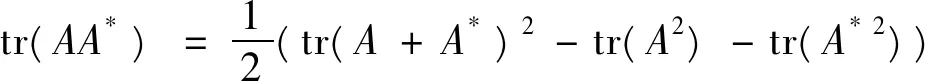
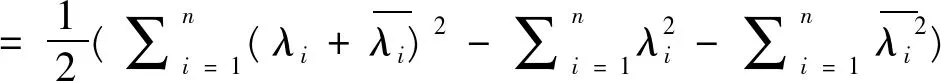
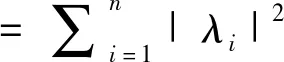
由引理2 (2)，A是正规矩阵；反之，若A是正规矩阵，由引理2 (1)，存在一个酉矩阵U∈Mn，使得U*AU=diag(λ1,λ2,…,λn)，于是，有

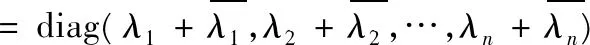
从而，(b)得证。

(c) 同(b)。

由(b)知，A是正规矩阵；反之，显然。

(e) 若tr(A*A)2=tr((A*)2A2)，由引理3，有tr(AA*)2=tr(A*A)2，于是

tr((A*A-AA*)*(A*A-AA*))

=tr((A*A-AA*)2

=tr(A*A)2-tr((A*)2A2)-tr(A2(A*)2)+tr(AA*)2=0

所以，A*A-AA*=0，即A*A=AA*，反之，显然。

(f)若(A*A)2=(A*)2A2，则tr(A*A)2=tr((A*)2A2)，由(e) 知A是正规矩阵；反之，显然。

定理2设A∈Mn，则矩阵A是正规矩阵当且仅当下述任一命题成立

(a)(Ax,Ax)=(A*x,A*x)对任意x∈Cn都成立；

(b)(Ax,Ay)=(A*x,A*y)对任意x,y∈Cn都成立；

证明(a) 因为内积恒等式

(Ax,Ax)=(A*x,A*x)⟺(Ax)*Ax=(A*x)*A*x

⟺x*A*Ax=x*AA*x

⟺(x,A*Ax)=(x,AA*x)

⟺(x,(A*A-AA*)x)=0。

此式对任意x∈Cn都成立当且仅当A*A-AA*=0，即A是正规矩阵。

(b) 若(Ax,Ay)=(A*x,A*y)对任意x,y∈Cn都成立，则令x=y，便得(a), 所以A是正规矩阵；反之，若A是正规矩阵，则有A*A=AA*，于是对任意x,y∈Cn，有

y*A*Ax=y*AA*x⟺(Ax,Ay)=(A*x,A*y)。

(c)由于|(Ax,x)|≤(|A|x,x)是酉不变量，即它成立当且仅当

|(U*AUx,x)|≤(|U*AU|x,x)，其中U为任一酉矩阵，并注意到|U*AU|=U*|A|U。 因此，使用引理1 , 可以假定A是上三角矩阵。

若A是正规矩阵，则上三角的正规矩阵一定是对角矩阵，不妨设A=diag(λ1,λ2,…,λn)，于是要证不等式等价于

后者显然成立。 反之，设|(Ax,x)|≤(|A|x,x)对任意x∈Cn都成立, 其中A是上三角矩阵。 下证A实际上是一个对角矩阵，从而A是正规矩阵。 下面对n=2的情形给出证明，一般情形应用数学归纳法证明即可。

[1] Horn R A, Johnson C R. Matrix analysis[M]. Cambridge: cambridge university press, 2013: 131-148.

[2] 陈景良，陈向晖．特殊矩阵[M]．北京：清华大学出版社，2001：144-153．

[3] 张 英．正规矩阵的判定及其性质[J]．重庆师范学院学报(自然科学版)，1998，15(4)：77-80．

[4] 姚光同，贾 璐．正规矩阵的一个等价条件[J]．松辽学刊(自然科学版)，2002，24(3)：67-68．

[5] 张 贺，袁 博．正规矩阵的几个等价条件[J]．河北北方学院学报(自然科学版)，2009，25(1)：9-13．

[6] 卢辛全，王玉良，胡江海．正规矩阵若干判定及性质[J]．阜阳师范学院学报(自然科学版)，2009，26(3)：4-6．

The Equivalent Characterization of the Normal Matrix

LIU Jun-tong

(SchoolofMathematicsandStatistics,FuyangNormalUniversity,FuyangAnhui236037，China)

The normal matrix plays a very important role in unitary similarity theory. The normal matrix is discussed by using Schur-lemma and unitary similarity from the eigenvalues, singular values and traces of the matrices. At the same time, several equivalent conditions about normal matrix are obtained.

normal matrix; unitary matrix; upper triangular matrix; trace

2015-04-19

阜阳师范学院精品课程(2012JCJY04)；安徽省教学研究项目(2013jyxm139)；阜阳师范学院基层教学组织建设项目(2013JCJS03)资助。

刘俊同(1982-)，男，硕士，讲师，研究方向：代数学、矩阵论。

O151. 21

A

1004-4329(2015)04-006-03

10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-006-03