一类具偏差变元的高阶泛函微分方程的周期解

汪代明

(阜阳师范学院 数学与统计学院，安徽 阜阳 236037)

一类具偏差变元的高阶泛函微分方程的周期解

汪代明

(阜阳师范学院 数学与统计学院，安徽 阜阳 236037)

具有偏差变元的泛函微分方程在生态学和控制论等领域有着广泛的应用。本文利用Mawhin重合度拓展定理和一些分析技巧，研究一类具有偏差变元的高阶泛函微分方程x(n)(t)+f(x′(t))+h(x(t))x′(t)+g(t,x(t-τ(t)))=p(t)，得到了周期解存在新的充分条件，推广了已有的若干结果。

周期解；重合度；偏差变元；泛函微分方程

泛函微分方程是描述带有时滞现象的数学模型。具有偏差变元的微分方程由于在生物学、经济学、生态学和人口动力系统等实际问题中应用广泛，而被人们广泛关注[1-10]。文献[1-4]分别研究了如下几种方程

x″(t)+f(x′(t))+g(x(t-τ(t)))=p(t)

(1)

x″(t)+f(x′(t))+h(x(t))x′(t)+

g(x(t-τ(t)))=p(t)

(2)

和 x(2n)(t)+h(x′(t))+f(x(t))x′(t)+

g(t,x(t-τ(t)))=p(t)

(3)

的周期解存在性问题。

受上述文献的启发，本文研究如下更具一般性的n阶方程的

x(n)(t)+f(x′(t))+h(x(t))x′(t)+

g(t,x(t-τ(t)))=p(t)

(4)

的周期解的存在性问题，其中n≥2,f,h,τ,

p:R→R和g:R×R→R为连续函数，τ(t),

p(t)为T周期函数，而g(t,x)是关于t的T周期函数。 利用Mawhin重合度拓展定理和一些分析技巧，在n≥2的情形下，得到了该方程周期解存在

的充分条件，从而推广和改进了文献[1-4]的相关结论。

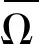
1)Lx≠λNx,∀x∈∂Ω∩Dom (L)，∀λ∈(0,1);

2)QNx≠0,∀x∈∂Ω∩Ker L;

3)deg{QN,Ω∩Ker L，0}≠0;

1 主要结果

定理1如果存在常数

r1≥0,r2≥0,H>0,K>0和D>0，使得下列条件成立：

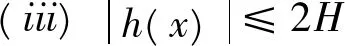
则当2Tn-1[r1+(T+1)r2+H]<1时，方程(4)至少存在一个T周期解。

证明考察如下方程x(n)(t)+λf(x′(t))+

λh(x(t))x′(t)+λg(t,x(t-τ(t)))=λp(t)，

λ∈(0,1)

(5)

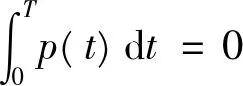
(6)

再由积分中值定理知∃ξ∈[0,T],使得

f(x′(ξ))+g(ξ,x(ξ-τ(ξ)))=0

(7)

先证存在t*∈[0,T],使得

(8)

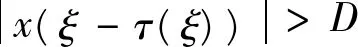
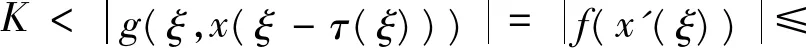
这是矛盾的，故

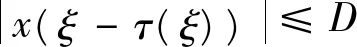
(9)

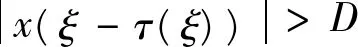
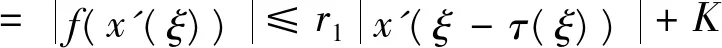
于是

(10)

由(9)式和(10)式知，无论r1=0还是r1>0，均有

(11)

由于ξ-τ(ξ)∈R,因而一定存在整数k和t*∈[0,T],使得ξ-τ(ξ)=kT+t*,故由(11)式得

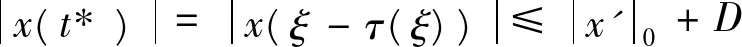
从而(8)式成立，由此得

(12)

令F(z)=2Tn-1[r1+(T+1)(r2+z)+H]<1，z∈(0,+∞). 由题设条件2Tn-1[r1+(T+1)r2+H]<1知，F(0)<1,又F(z)在[0,∞)上连续，因而存在常数δ>0,使得

F(z)=2Tn-1[r1+(T+1)(r2+z)+H]

<1，z∈(0,δ)

(13)

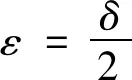
F(z)=2Tn-1[r1+(T+1)(r2+ε)+H]<1

(14)

对上述ε>0，由题设条件(iv)知，一定存在与λ和x无关的常数ρ≥D，使得

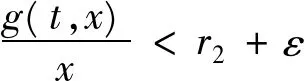
(15)

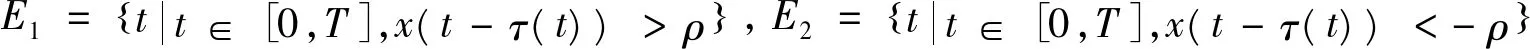
(∫E1+∫E2+∫E3)g(t,x(t-τ(t)))dt

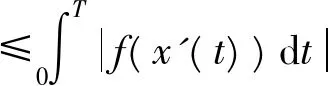
即

(16)

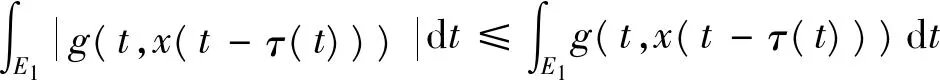
(17)

由E2,E3的定义和(15)式知，

(18)

(19)

，

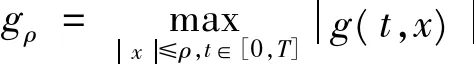
x(0)=x(T)知，一定存在η∈[0,T]，使得x′(η)=0,从而有

……，

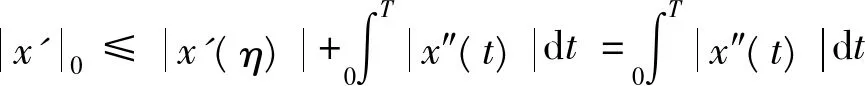
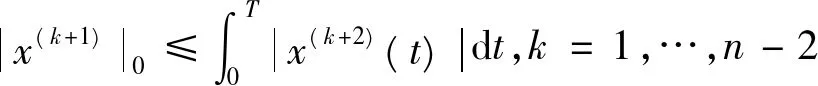
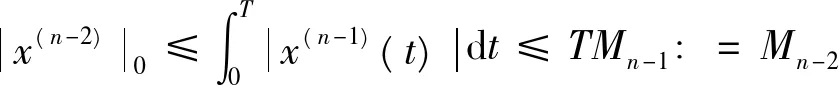
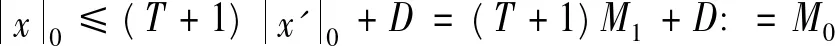
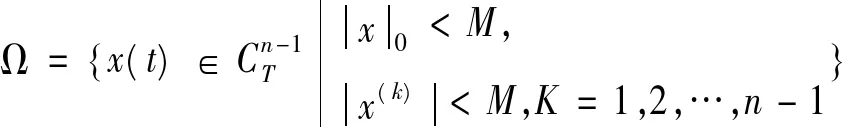
显然Ker L=R。定义投影算子P和Q分别为：

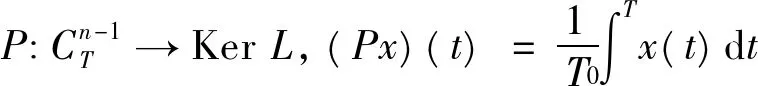
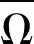
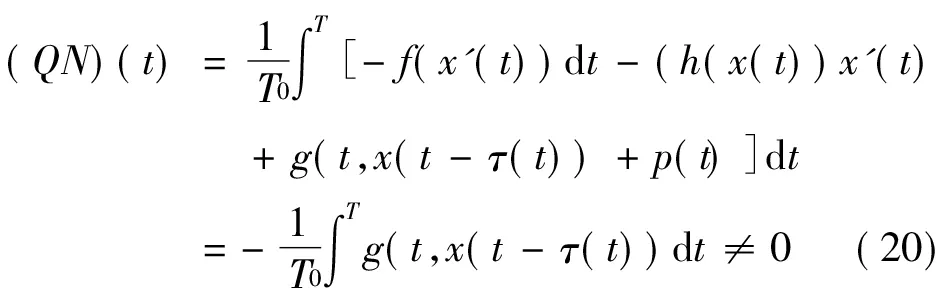
引理1的条件3)满足。因此，根据引理1知，方程(4)至少存在一个T周期解。

推论1如果存在常数r1≥0,r2≥0,H>0,K>0和D>0，使得下列条件成立：

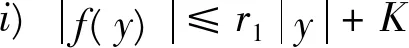
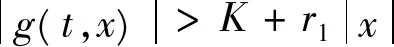
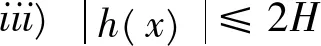
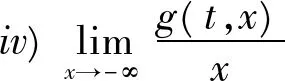
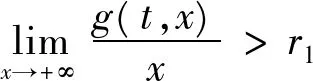
则当2Tn-1[r1+(T+1)r2+H]<1时，方程(4)至少存在一个T周期解。

类似于定理1的证明，可得如下结果：

定理2如果存在常数r1≥0,r2≥0,H>0,K>0和D>0，使得下列条件成立：

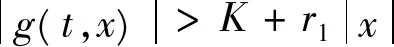
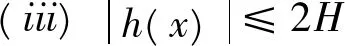
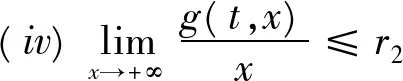
则当2Tn-1[r1+(T+1)r2+H]<1时，方程(4)至少存在一个T周期解。

2 应用举例

作为应用考虑下列方程

g(x(t-sint))=cost

(21)

其中，

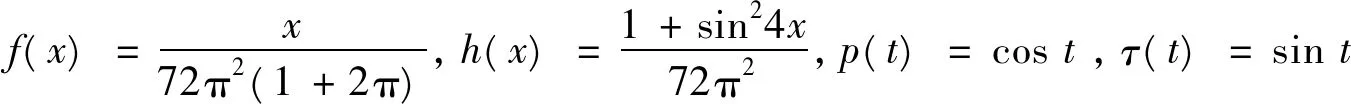
2Tn-1[r1+(T+1)r2+H]

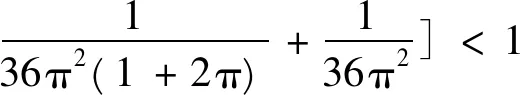
因而，根据本文推论1知方程(21)至少存在一个T周期解。而上述结果不能由文[1-4]得到，因此本文的研究推广和改进了文[1-4]的主要定理。

[1] 鲁世平，葛渭高，郑祖庥．具偏差变元的Rayleigh方程周期解问题[J]．数学学报，2004，47(2)：299-304．

[2] 杜 波．一类具偏差变元的二阶微分方程周期解[J]．安庆师范学院学报(自然科学版)，2006，40(2)：12-14．

[3] 刘道金，鲁世平．一类具偏差变元的二阶微分方程周期解[J]．杭州师范大学学报(自然科学版)，2009，8(5)：354-357．

[4] 汪小明，孙杨剑．一类具偏差变元的高阶泛函微分方程的周期解[J]．西北师范大学学报(自然科学版)，2013，49(3)：16-19．

[5] 施吕蓉，周宗福，高 伟．一类三阶具多偏差变元微分方程的周期解[J]．重庆工商大学学报(自然科学版)，2013，30(1)：6-9, 15．

[6] 陈新一．具偏差变元高阶泛函微分方程周期解的存在定理[J]．西北民族大学学报(自然科学版)，2013，34(2)：1-7．

[7] 欧伯群，秦发金．一类n阶中立型泛函微分方程周期解的存在唯一性[J]．天津师范大学学报(自然科学版)，2013，33(3)：22-27．

[8] 沈钦锐．一类三阶多时滞微分方程周期解的存在唯一性[J]．厦门大学学报(自然科学版)，2014，53(3)：299-304．

[9] 陈文斌，高 芳，鲁世平．一类时滞微分方程周期解的存在性[J]．四川大学学报(自然科学版)，2014，51(3)：455-458．

[10]WangXM.NewresultsonperiodicsolutionsforaclassofRayleightype-Laplacianequationswithdeviatingarguments[J].NonlinearOscilllations, 2012, 15(3): 331-336.

[11]GainsRE,MawhinJL.Coincidencedegreeandnonlineardifferentialequations[M].Heidelberg:Springer-Verlag, 1977: 95-169.

Existence of periodic solutions for a kind of higher order functional differential equations with a deviating argument

WANG Dai-ming

(School of Mathematics and Statistics, Fuyang Normal University, Fuyang Anhui 236037, China)

Functional differential equations with deviating arguments have been widely used in fields such as ecology and control theory. By employing the Mawhin coincidence degree theory and some analysis techniques, a kind of higher order functional differential equations with a deviating argument as follows x(n)(t)+f(x′(t))+h(x(t))x′(t)+g(t,x(t-τ(t)))=p(t),is studied, and some sufficient conditions on the existence of periodic solutions is given, which generalizes and improves some known results.

periodic solution; coincidence degree; deviating arguments; functional differential equation

2015-8-12

安徽省高校省级自然科学研究项目(KJ2011Z290)资助。

汪代明(1979-)，女，硕士，副教授，研究方向：微分方程。

O175.12

A

1004-4329(2015)04-025-04

10.14096/j.cnki.cn34-1069/n/1004-4329(2015)04-025-04