伺服驱动压边力控制系统建模与仿真

伺服驱动压边力控制系统建模与仿真

杨莉王国佐邹凤刚秦泗吉

燕山大学，秦皇岛，066004

摘要：将伺服驱动技术应用于压边力控制，可以更有效地控制拉深成形过程，提高成形效果。采用伺服电机驱动的压边力控制系统由机械和数控系统两部分组成，系统参数匹配的合理性对压边力控制的动态性能影响较大，而系统的动态性能直接影响到压边力控制精度和效果。首先对双滑块六杆机构输入输出方程进行了线性化处理，建立了机械系统、数控伺服系统的数学模型，得到了压边力控制系统的数学模型和仿真模型，对控制系统进行了仿真分析，初步确定了控制系统的位置环PID参数。最后根据仿真分析结果进行了压边力控制实验系统的参数设定，实验表明，根据仿真值稍作调整就能达到实验系统的控制要求，大大缩短了系统调试时间。

关键词：压边力控制；伺服驱动；数学模型；PID控制；系统仿真

中图分类号：TG385.9

收稿日期：2014-11-26

基金项目：国家自然科学基金资助项目(51175451)

作者简介：杨莉，女，1962年生。燕山大学机械工程学院副教授、博士。研究方向为先进制造、数控重载驱动技术。王国佐，男，1989年生。燕山大学机械工程学院硕士研究生。邹凤刚，男，1988年生。燕山大学机械工程学院硕士研究生。秦泗吉，男，1963年生。燕山大学机械工程学院教授、博士。

Modeling and Simulation of Servo-driven BHF Control System

Yang LiWang GuozuoZou FenggangQin Siji

Yanshan University,Qinhuangdao，Hebei,066004

Abstract:Servo-driven control technology of BHF is more effective and can improve the forming effect in deep drawing process. BHF control system driven by servo motor was composed of the mechanical system and CNC system. The parameters of components in BHF system had a greater influence on the dynamic performance of the system, so it could have effects on accuracy and efficiency in BHF control. Firstly linearization of the input and output equations was made for the six-bar linkage and the double-slider mechanism. And mathematical models of mechanical system and CNC control system were obtained respectively. Then performance of the system was simulated and analyzed and the PID parameters of the position loop were adjusted. Finally, the parameters in the experiments of the BHF control system were given based on simulation results. The experimental results show that it can meet the requirements of the BHF control to adjust slightly the values of the parameters of the control components based on the modeling and simulation results, so the debug time of system control parameters can be shorten greatly.

Key words: blank holder force(BHF) control; servo drive; mathematical model; PID control; system simulation

0引言

拉深成形是板材成形中的典型工艺之一，在

生产中的应用非常广泛。在成形过程中，通常将控制压边力作为控制成形过程的主要手段[1]。板坯在成形过程中的各个阶段所需要的压边力是不同的，如果在各变形阶段都施加相同的压边力，就可能出现在某个变形阶段因压边力太小而使得起皱趋势严重，而在另外的变形阶段压边力过大导致某个部位出现破裂的危险[2]。在变压边力控制过程中，压边力参数的合理取值、调整和控制，成为控制金属流动、防止出现起皱和破裂的最重要的手段之一[3-5]。

在理想情况下，拉深成形过程中的压边力是随行程和位置同时变化的。但目前在生产实际中，采用通用压力机或专用压力机的成形，一般都不能满足这样的工艺要求，所以开发与拉深工艺要求相适应的、随行程和位置同时变化的变压边力控制技术是非常必要的。

液压传动方式具有传力大、易于控制等优点，可用于大中型压力机上的变压边力控制。变压边力控制系统是由比例溢流阀控制液压缸内的压力而实现控制过程的[6]。这种控制系统结构复杂、响应时间慢、能耗高。

随着控制技术的不断发展，特别是计算机及其相关技术的发展，数控技术在成形领域得到了越来越多的应用。根据拉深工艺对压边力的要求，文献[7]提出了以伺服电机作为驱动元件实现数控压边的方法。这种压边力控制方法采用伺服电机驱动，配以适当的压边力执行机构，对压边过程中压料板的位置、速度、力等进行精确控制，使压边力按预先设定的规律随拉深行程变化，实现不同的拉深工艺要求，达到控制目的。

笔者在前期工作[8-9]中，主要对应用于不同工艺形式的压边力执行机构进行了研究，确定了机构构型和杆系尺寸。在此基础上，还需要对整个控制系统进行建模和仿真，分析系统的性能，以便构建系统的实验平台。

伺服驱动压边力控制系统由数控系统和机械系统组成，这两部分系统参数的合理匹配是整个控制系统得以良好运行的保证。本文以所研制的压边力控制系统为基础，对压边力控制系统进行了建模、仿真，确定了系统控制器参数，为实验系统的PID参数设定提供了依据，这种方法可显著缩短系统调试时间。

1压边力控制系统的数学模型

1.1系统组成及原理

图1为伺服驱动压边力控制系统组成框图，其中数控系统包括上位机PC、下位机运动控制器、伺服电机、驱动器、位移和力检测装置等。机械系统由联轴器、丝杠螺母副、六杆机构、压料板、缓冲件和连接件等组成(图2)。PC通过标准PCI总线连接具有实时控制功能的运动控制器，组成完整的数控装置，数控装置发出指令信号经伺服驱动器转换和放大后使电机转动，伺服电机驱动丝杠螺母副和六杆机构带动压料板实现给定的压边运动，电机内置脉冲编码器用于检测电机转角和转速，并实现反馈，力检测装置用于压边力的测量。

图1　伺服驱动压边力控制系统组成框图

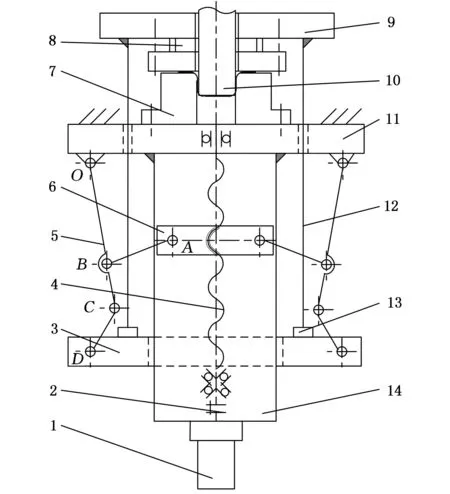
1.伺服电机　2.联轴器　3.下滑板　4.滚珠丝杠　5.六杆机构 6.螺母　7.凹模　8.测力环　9.压料板组件　10.凸模 11.垫板　12.连接杆　13.缓冲件　14.连接板 图2　伺服驱动压边力控制机械系统示意图

1.2双滑块六杆机构数学模型

1.2.1双滑块六杆机构输入和输出关系

如图2所示，六杆机构以螺母的匀速运动为输入，以压料板的变速直线运动为输出，其输入与输出运动关系可按图3所示的六杆机构简图以及给定相应参数导出。

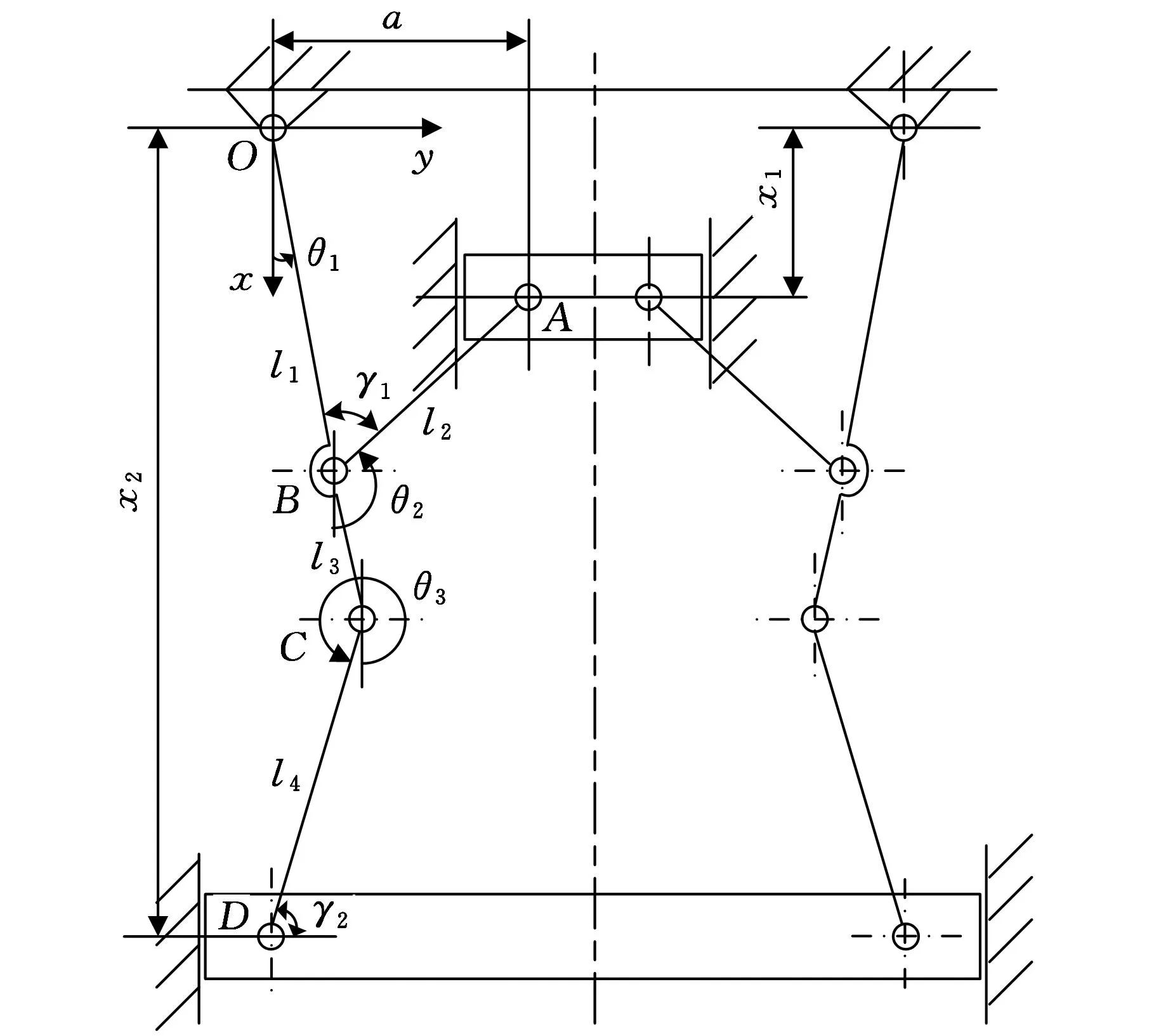
图3　六杆机构简图

如图3所示，输入滑块为螺母，输出滑块为下滑板。可以认为，六杆机构由两个四杆机构组成，上滑块、杆AB、杆OB和机架组成一四杆机构，其中杆AB与上滑块(输入滑块)相连。杆BC、杆CD、下滑块和机架组成另一四杆机构，其中杆CD与下滑块(输出滑块)相连，图中杆OB和杆BC为刚性连接。

设杆OB、杆BA、杆CD与x轴夹角分别为θ1、θ2、θ3，OB、BA、BC、CD对应的各杆长度尺寸分别为l1、l2、l3、l4，输入滑块与固定铰接点O的水平距离为a。图3中x1、x2分别为输入和输出滑块至点O的垂直距离，它们与θ1之间的关系为

(1)

(2)

六杆机构输入与输出关系可由以θ1为参数的式 (1)和式 (2)确定，其输入与输出关系为非线性关系，图4所示为六杆机构输入与输出关系曲线。

1.2.2双滑块六杆机构的线性化处理

因六杆机构的输入与输出关系是非线性的，为了简化建模和仿真，需进行线性化处理。

若输入为x1、输出为x2，设输入输出关系为

x2=f(x1)

(3)

若给定输入点位置x10，对应输出点位置x20，将式(3)展开成泰勒级数:

(4)

(5)

(6)

对正装模具结构，因压边力施加阶段的工作行程很小，可在工作点附近，将六杆机构的输入和输出关系作为线性环节来处理。略去式(4)中(x1-x10)2项及其后面的高阶项，得增量方程Δx2=kdΔx1，为简化起见，省去增量符号Δ，增量方程改写为[10]

x2=kdx1

(7)

式中,kd为比例系数。

其传递函数为

(8)

当压边工作点位置不同时，kd也不相同。

若压边行程在100～130mm范围内，其对应的输入与输出二阶导数关系曲线如图5所示。随着压边行程的增大，二阶导数的绝对值越来越小，线性化程度也越来越好。若将工作点取x10=124.5mm，计算得出，该位置的输入与输出关系二阶导数值小于0.005mm，说明该工作点附近线性化程度较好。

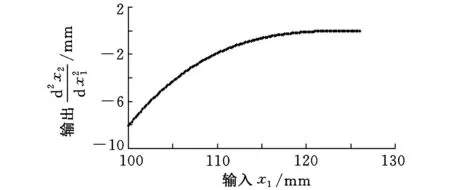
图5　六杆执行机构输入与输出二阶导数关系曲线

1.3丝杠螺母副数学模型

丝杠螺母副以伺服电机的角位移为输入，以螺母的直线位移为输出，其动力平衡方程式为

(9)

式中，m为螺母等执行部件的质量；B1为导轨副上黏性阻尼系数；FL为作用在螺母上的外载荷；Fp为螺母执行部件的驱动力，Fp=k(x0-x1)；k为折算到丝杠轴上的传动系统刚度；x1为螺母的直线位移；x0为电机对螺母执行部件的输入位移，x0=Lθ/(2π)；θ为电机轴转角；L为滚珠丝杠导程。

滚珠丝杠副传动系统的刚度，可认为是与滚珠丝杠相关联的零部件刚度的串联总和，计算公式如下：

(10)

式中，ks1为丝杠轴拉压刚度；kb为支承轴承的轴向接触刚度；kc为滚珠与滚道的接触刚度；kr为折合到滚珠丝杠副上的伺服刚度；kbr为轴承座的刚度；knr为螺母座的刚度；kt为联轴器的刚度；ks2为滚珠丝杠副扭转刚度折合到执行部件的直线刚度。

式(10)中后几项与前3项相比影响较小，实际计算时取前3项。

对式(9)进行Laplace变换得

(11)

以θ(s)为输入，以x1(s)为输出，不考虑外力FL时，其传递函数为

(12)

1.4伺服驱动系统的数学模型

压边力控制系统选用交流永磁同步伺服电机作为驱动元件，永磁同步电机在矢量控制条件下与直流电机是等价的，只是将电枢电流换成了与转子磁链正交的交流电流分量iq，永磁同步电机的电压平衡方程为

(13)

式中，Uq为电机电枢电压；iq为电枢电流；L0为电枢电感；R为电枢电阻；E为电机反电势，E=keω；ke为电机电势系数；ω为转子角速度。

电机轴上的转矩平衡方程为

(14)

式中，Mm为电机输出转矩，Mm=kTiq；kT为电机转矩系数；ML为负载转矩；B2为等效到电机轴上的黏性阻尼系数；J为折算到电机轴上的总转动惯量。

若不考虑电机负载转矩，将式(13)、式(14)整理后进行Laplace变换，得

以Uq(s)为输入，ω(s)为输出，其传递函数为

(15)

2压边力控制系统的仿真

2.1仿真模型

将伺服驱动系统和机械系统的数学模型综合起来，并引入速度环和位置环，得到图6所示的压边力控制系统的数学模型，其中，Kv1、Ti分别为速度环增益和积分时间参数，Kp2、Kv2、Ki2分别为比例、微分、积分增益。

利用仿真技术可以实现对系统动态性能的分析[11]，并找到各参数间的匹配关系，因此借助动态系统仿真工具MATLAB/Simulink，对压边力控制系统建模，在空载且不计六杆机构与导杆摩擦情况下，系统仿真模型如图7所示。

图6　压边力控制系统模型

图7　压边力控制系统仿真模型

压边力控制系统参数整定主要在速度环和位置环参数的匹配上，速度环在伺服驱动器内实现，通过电机上的脉冲编码器反馈电机转速信号构成，采用的是比例积分控制；位置环由运动控制器来完成，位置环是通过电机上的脉冲编码器反馈电机转角信号而构成的，采用典型的比例积分微分控制。

2.2仿真参数

根据所研制的压边力控制系统，给定仿真模型的参数如表1所示，不考虑电机轴的阻尼力矩，选取工作点x10=100.7mm，计算kd=0.05，对压边力控制系统性能的影响进行仿真分析。

表1　仿真模型已知参数

由图5和上文的分析可见，工作点坐标位置大于所选取的工作点x10时，其输入输出关系的线性化程度会更好。

2.3压边力控制系统的仿真分析

综合考虑系统的快速性和稳定性要求，根据表1参数值和压边力控制系统的仿真模型，对压边力控制系统进行PID参数仿真整定，得到整定参数如表2所示。当系统输入为单位阶跃信号r(t)时，得到系统的阶跃响应信号c(t)(图8)，从响应曲线看，系统具有较好的动静态性能。

表2　仿真整定参数

图8　系统阶跃响应信号

当改变工作点位置后，仍可按上述方法进行处理，仿真得到PID参数。

3压边力控制系统的实验

图9所示为所研制的数控系统和机械系统的部分组成，数控系统由PC、GE-200-SV-PCI运动控制器、SGMGH-20ACA61伺服电机、SGDM-20ADA驱动器、力检测装置及接口电路等组成，其中运动控制器附件端子板10连接运动控制器和伺服驱动器11，驱动器11与伺服电机1相连，电机内置增量式光电脉冲编码器。机械部分由六杆机构2和丝杠螺母副3等组成。

(a)机械系统(b)数控系统 1.伺服电机　2.六杆机构　3.丝杠螺母副　4.凹模　5.测力环 6.压料板　7.凸模　8.开关电源　9.伺服变压器 10.端子板　11.伺服驱动器 图9　压边力控制实验系统

将伺服电机的驱动器设置为速度控制方式，按仿真结果，设置速度环增益Kv1为40，积分时间常数Ti为20，仿真值与伺服驱动器出厂设置一致。

在电机调整好后，对运动控制器进行调试，设置±10V的模拟量输出。不考虑前馈控制，速度前馈增益Kvff、加速度前馈增益Kaff设置为0，主要对比例Kp2、微分Kv2、积分增益Ki2三个PID基本参数进行设置。

根据表2仿真整定参数值，对实验系统进行调试，设置压边力控制系统各参数的变化范围为Kp2(2～8)、Kv2(0～9)、Ki2(12～26)。实验时先确定Kp2，然后改变Kv2和Ki2，进行压边力加载实验，结果表明Kp2对系统影响最大，当Kp2取8时电机产生振动；改变微分增益Kv2和积分增益Ki2对系统影响不显著。表3为实验系统中运动控制器调节后的PID参数值，该参数下系统的快速性和稳定性最佳。

表3　运动控制器PID参数

仿真得到的PID参数值，为实验系统提供了参考依据，有效地缩短了调试时间。但是机械系统的摩擦、间隙和阻尼会影响系统性能，实验系统PID参数与仿真结果相比稍有变化。

4结论

(1)在所选取的工作点，根据压边力的加载行程小和输入输出函数的特点，对六杆执行机构的输入和输出关系进行了线性化处理。当工作点改变后，选取不同的比例系数kd，也可作类似的线性化处理。

(2)对压边力控制系统的数控系统、机械系统进行了数学建模，进一步建立了控制系统的数学模型和仿真模型，在保证系统具有良好的动态性能和稳态精度的前提下，仿真得到了PID参数。

(3)利用仿真得到的PID参数对压边力控制实验系统进行了参数设定，仿真为实验系统PID参数设定提供了依据，减少了系统调试时间。

参考文献：

[1]DemirciHI,YaarM,DemirayK,etal.TheTheoreticalandExperimentalInvestigationofBlankHolderForcesPlateEffectinDeepDrawingProcessofAl1050Material[J].Materials&Design, 2008, 29(2): 526-532.

[2]ZhangWenfeng,ShivpuriR.ProbabilisticDesignofAluminumSheetDrawingforReducedRiskofWrinklingandFracture[J].ReliabilityEngineering&SystemSafety, 2009, 94(2): 152-161.

[3]SeniorBW.FlangeWrinklinginDeep-drawingOperations[J].JournaloftheMechanicsandPhysicsofSolids, 1956, 4(4): 235-246.

[4]SiegertK,DannenmannE,WagnerS,etal.Closed-loopControlSystemforBlankHolderForcesinDeepDrawing[J].CIRPAnnals-ManufacturingTechnology, 1995,44(1): 251-254.

[5]RodriguesDM,LeitaoC,MenezesLF.AMulti-stepAnalysisforDeterminingAdmissibleBlank-holderForcesinDeep-drawingOperations[J].MaterialsandDesign,2010,31:1475-1481.

[6]赵军. 圆锥形件拉深成形智能化的研究[D]. 哈尔滨:哈尔滨工业大学,1997.

[7]秦泗吉. 压边力控制技术研究现状及伺服数控压边方法可行性探讨[J].中国机械工程，2007, 18(1):120-125.

QinSiji.State-of-the-artofBlankHoldingForceControlTechnologyandFeasibilityofNumericalServo-controlHolding[J].ChinaMechanicalEngineering，2007, 18(1):120-125.

[8]杨莉，秦泗吉，杜广杰. 复合伺服驱动压边力控制方法及执行机构设计[J].中国机械工程，2012, 23(6):1360-1363.

YangLi,QinSiji,DuGuangjie.ACompositeControlTechniqueofBHFDrivenbyServeoMotorandDesigmfortheActuator[J].ChinaMechanicalEngineering，2012, 23(6):1360-1363.

[9]杨莉，金振林，秦泗吉,等. 复合伺服驱动压边力控制执行机构建模与优化[J].机械工程学报，2015,51(3):139-145.

YangLi,JinZhenlin,QinSiji,etal.ModelingandOptimizationofCompositeandServo-drivenActuatorforBlank-holderForceControl[J].JournalofMechanicalEngineering，2015,51(3):139-145.

[10]邹伯敏.自动控制理论[M].北京：机械工业出版社，1999.

[11]EbrahimiM,WhalleyR.Analysis,ModelingandSimulationofStiffnessinMachineToolDrives[J].Computers&IndustrialEngineering, 2000, 38(1): 93-105.

(编辑郭伟)