一种基于能量守恒原理的数控车削能耗模型
黄拯滔1张超勇1罗敏2谢阳1周志恒1
1.华中科技大学,武汉,4300742.湖北汽车工业学院,十堰,442002
摘要:根据机床系统的能量守恒原理,提出了一种数控车床加工过程能耗精确评估方法。参照机床系统的能量流分布,分离各能量分支的功耗,对各分支分别独立建模,最终建立数控车床系统能耗与主轴转速、进给量和材料去除率之间的函数关系。由于各分支系统建模的独立性,使得能耗模型不仅适用于数控车床系统稳定切削阶段,也适用于稳定的待机、空转和空切阶段。实验结果显示,车削过程能耗评估精度超过98%。在该方法的基础上,进一步提出改进型的机床系统单位体积能耗模型。
关键词:能耗模型;能量守恒;机床系统;车削过程;单位体积能耗
中图分类号:TH186
收稿日期:2014-07-11
基金项目:国家自然科学基金资助重点项目(51035001);国家自然科学基金资助项目(51275190);中央高校基本科研业务费专项资金资助项目(2014TS038)
作者简介:黄拯滔,男,1990年生。华中科技大学机械科学与工程学院硕士研究生。主要研究方向为离散制造车间高效低碳运行和智能优化算法。张超勇,男,1972年生。华中科技大学机械科学与工程学院副教授。罗敏,男,1967年生。湖北汽车工业学院电气与信息工程学院教授。谢阳,男,1987年生。华中科技大学机械科学与工程学院博士研究生。周志恒,男,1991年生。华中科技大学机械科学与工程学院硕士研究生。
An Assessment Model of Energy Consumption for NC Turning Process
Based on Principle of Conservation of Energy
Huang Zhengtao1Zhang Chaoyong1Luo Min2Xie Yang1Zhou Zhiheng1
1.Huazhong University of Science and Technology,Wuhan,430074
2.Hubei University of Automotive Technology,Shiyan,Hubei,442002
Abstract:Based on the principle of conservation of energy,an accurate assessment model of energy consumption for NC turning operation was presented. According to the energy flow of machine tool system, the power of each energy branch was separated. After modeling every branch, a function was built among energy consumption and spindle speed, feed rate and material removal rate.Because of the independence of these branches, the energy consumption model suited to the stable cutting stage,and to the stable standby and idle and cutting-free stages.The accuracy of this method is confirmed over 98% by a series of turning experiments.On the strength of this method, an improved model of specific energy consumption was developed.
Key words:model of energy consumption;conservation of energy;machine tool system;turning process;specific energy consumption
0引言
由于温室效应和雾霾现象对人们生活的影响日益严重,减少碳排放正日益成为全世界最为关注的话题。2008年,我国CO2排放量占世界排放总量的21.8%,已成为世界上排放CO2最多的国家。中国统计年鉴[1]显示,2012年中国能源消费达361 732万吨标准煤,CO2排放量达到79 541万吨。能源消费直接导致了碳排放,因而减少能源消费、提高能量利用率成为减少碳排放的主要突破口。在能源消费市场,制造业无疑占据了极大的比重,2012年我国制造业能耗占据全国能源消费总量比重超过50%。我国制造行业机床保有量世界第一,有800万台左右。若每台机床额定功率平均为10kW,我国机床装备总的额定功率为8000万kW,是三峡水电站总装机容量2250万kW的3倍多[2]。
机械加工行业能耗巨大,但是能量效率却十分低下,在节能减排上存在巨大的潜力和广阔的空间。Detmair等[3]的研究表明,在简单铣削过程中,仅有25%的能量用于切削工艺过程,其他75%的能量都被“浪费”在铣床及其辅助设备之上。Gutowski等[4]的铣削实验数据显示:一条自动化生产线能量效率甚至只有14.8%。Abele等[5]通过研究证实,在一个车削系统中,输入电能的65%被机床本身消耗,而车削工艺仅消耗输入电能的5%。
建立完善、精确的机床系统加工过程能量模型,不仅可以明确加工过程机床系统的能量源分布,指导设计者在改进机床系统设计方案的过程中采用更加完善的设计策略和更加节能的组件,而且有助于使用者选择恰当的机床型号,设计合理的加工工艺,设置高效的切削参数。一个精确的机床系统加工过程能量模型可以在机床系统能量输入和能量效率两个方面节省能源。研究机床系统加工过程能量模型,对机械加工制造业节能具有重要意义,已经成为当前研究的热点。
单位体积能耗(specific energy consumption,SEC)是指去除单位体积材料时的能量消耗,它是表征系统能量效率的重要参数。对于机床系统而言,由于去除材料的切削功率就是机床的有效输出,因此SEC既体现了输入功率Pi的能量利用率,也表征了输入功率Pi转移到工件中的能量转化率。本文以数控车床为平台,从机床系统的输入功率Pi着手,力图更加全面地分析车床系统能量流向,寻找输入功率Pi与切削参数、材料去除率之间的联系,构建精确的输入功率Pi的函数。在此基础之上,建立了完善的车床系统加工过程单位体积能耗SEC模型,为下一步工艺过程优化、切削参数选取奠定基础。
1研究背景
机床系统SEC即去除单位体积金属材料时机床系统消耗的能量,Li等[6]认为SEC可以表示如下:
(1)
在稳定切削阶段,式(1)可以表示为
(2)
式中,Q为加工过程能耗;V为加工过程去除的金属材料体积;ηMRR为材料去除率(material removal rate,MRR),即单位时间内去除的金属材料体积。
对于外圆车削过程有如下关系:
(3)
式中,f为进给量,mm/r;ap为切削深度,mm;vc为切削速率,m/min。
对于稳定切削过程,建立单位体积能耗模型的难点在于构建精确的机床系统输入功率Pi模型。由于车床系统本身结构的复杂性,以及刀具磨损、切削环境温度改变造成的切削过程动态性,使得机床系统输入功率Pi建模变得十分困难,至今仍然没有一个公认的、准确的Pi模型。
传统上,机床系统稳定切削阶段的输入功率Pi模型均由Gutowski等在文献[4]中所提出的模型发展而来。文献[4]通过大量实验证实输入功率Pi可分为两个部分:固定功率和可变功率。其中可变功率与材料去除率之间存在正比例的函数关系。输入功率Pi表达式为
Pi=P0+kηMRR
(4)
式中,P0为机床系统待机功率,W;k为常数,J/mm3。
Gutowski等[4]认为P0是由机床系统结构特性决定的,它消耗在机床系统的控制、冷却、润滑、照明等辅助设备中,对同一机床是固定值。待机功率P0在多数机床系统中甚至超过输入功率Pi的60%,Li等[7]通过综合分析6类数控机床的待机功率P0,得出图1所示的待机功率P0分解图。参数k则是由工艺、刀具、零件材料、机床特性决定的常数。Gutowski等[4]认为ηMRR是决定机床输入功率Pi的主要变量,其单位为mm3/s。
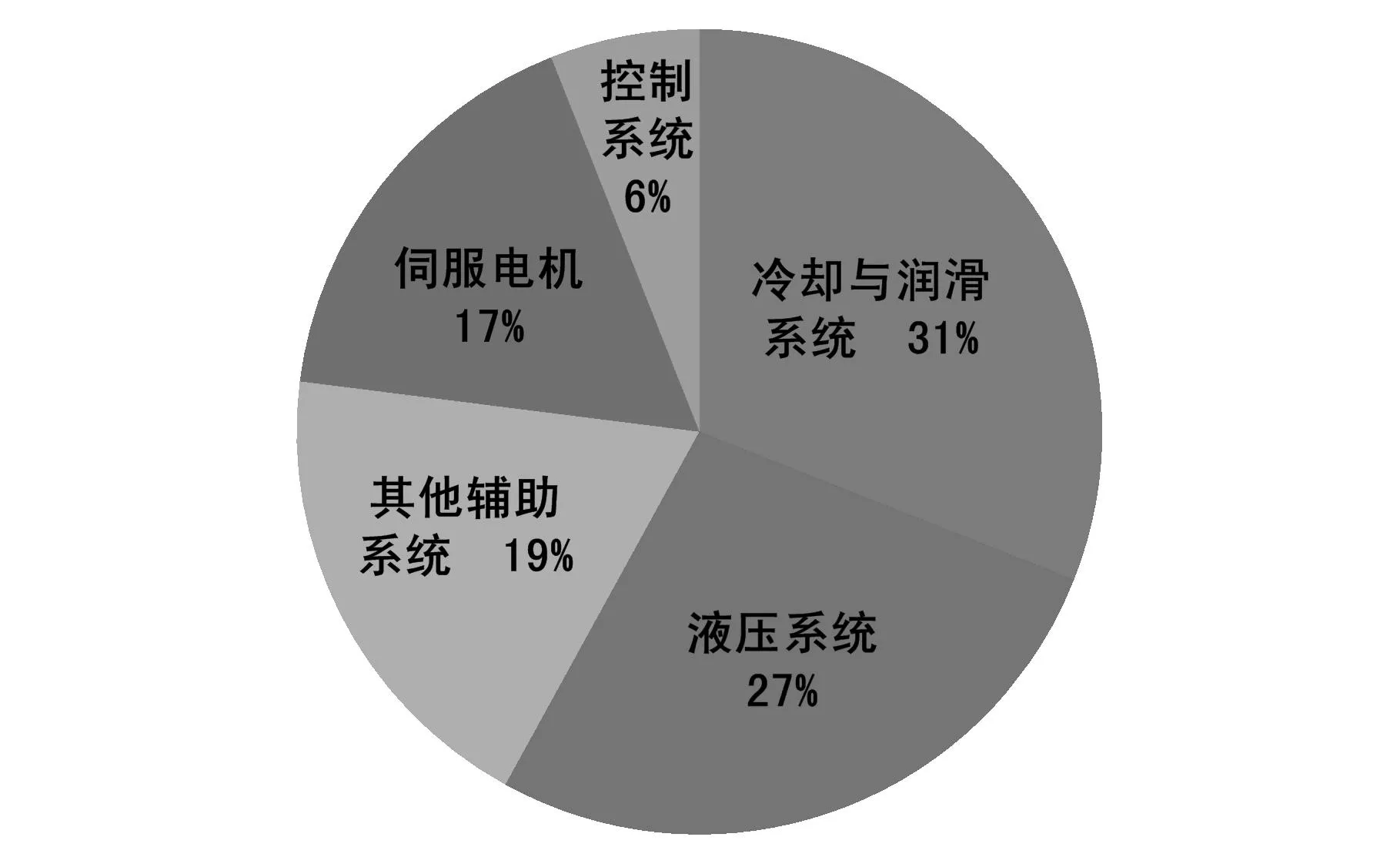
图1 待机功率P 0分解图
然而,近年来一些学者通过研究发现,材料去除率并不是决定机床系统可变功率的唯一变量。陈宁[8]通过实验发现,在同一实验条件下,即使材料去除率相同,机床系统的输入功率Pi也不一样。Li等[9]的实验数据也证实了上述观点。显然,Gutowski等[4]所提出的机床系统输入功率Pi一次函数模型仅仅是从实验采集的功率数据通过数学方法拟合得到,并没有严谨的理论基础。
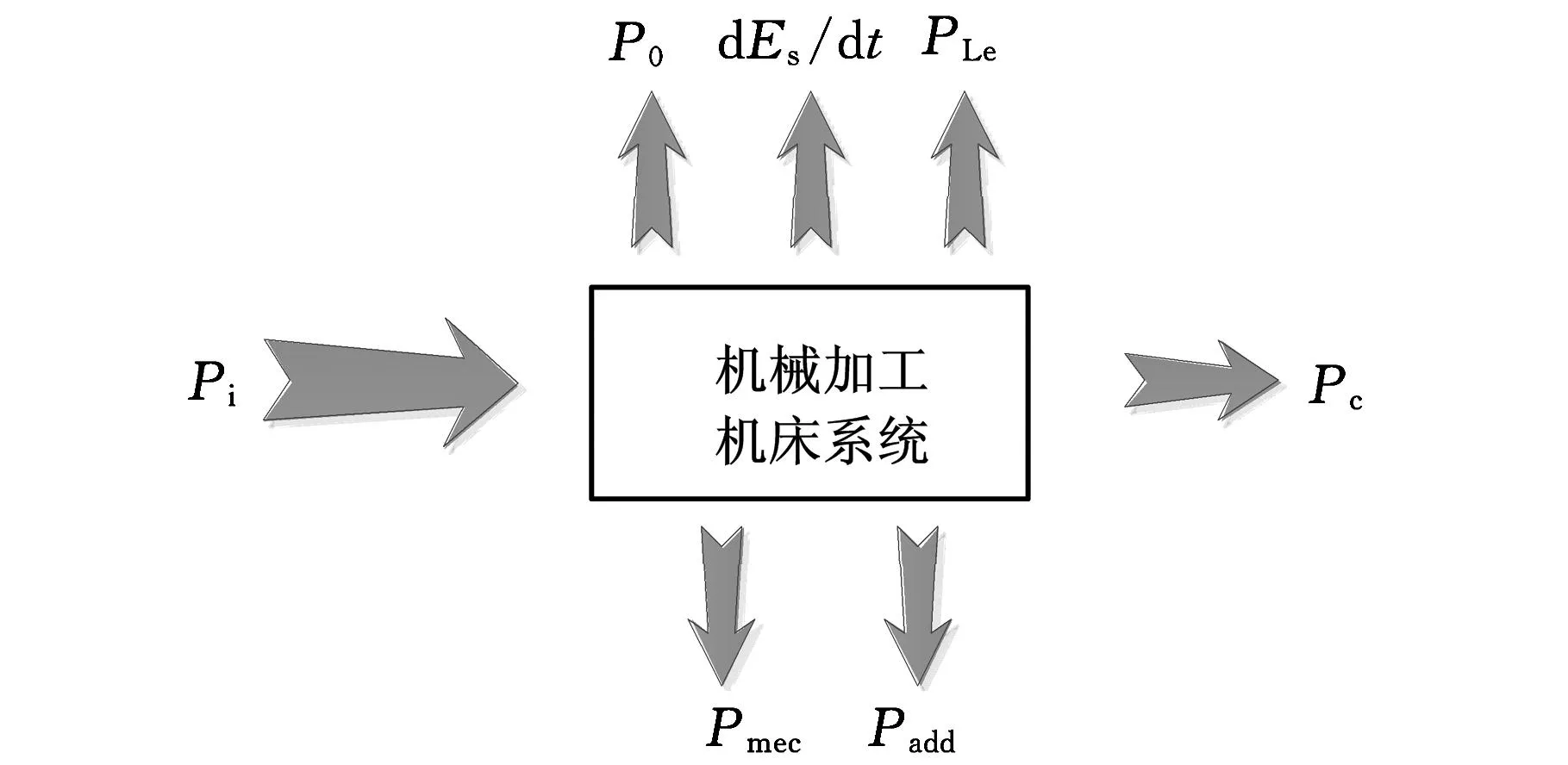
图2 机床系统能量流向
此后,学者们开始尝试从机床系统能量流向的角度来建立输入功率Pi的模型。机床系统的加工过程是一个能量传递与转化的过程,这个过程包含能量的输入、存储或释放、损耗和输出(图2)。机床系统的输入能量即电能,其输入功率Pi可以由电气柜上的测点实时测量得到。存储或释放的能量Es即电机的电磁势能、机械系统的动能,在稳定切削阶段机床系统存储或释放的能量基本保持不变。损耗功率ΔP由4个部分组成:与机床工作状态无关的待机功率P0,用于支撑外围辅助设备的运转,使机床系统保持预备状态;与电机工作状态和载荷情况密切相关、机理复杂的电机电损PLe[10],该部分能量转化为铁芯和绕组的焦耳热;与加工过程切削要素相关的机械损耗Pmec,该部分能量在传动链上被转换成热能;与切削载荷相关的附加载荷损耗Padd,该部分能量被消耗在传动系统的摩擦发热、振动及噪声上。机床系统的输出能量则被用来使切屑发生形变并从工件表面被移除,其功率即切削功率Pc。
按照机床系统能量守恒的原理,机床系统输入功率Pi可以表达为
(5)
在稳定切削过程中,机床系统的存储或释放的能量基本保持不变:
(6)
所以,稳定切削阶段机床系统的输入功率
Pi=P0+PLe+Pmec+Padd+Pc
(7)
2理论建模
数控车床系统切削过程可大致分为以下几个步骤:开机运行—主轴启动(空转阶段)—进给启动(空切阶段)—切削—进给停止—主轴停转—停机。数控车床系统的工作状态可以从它的功率曲线分辨。图3是CK60数控车床典型切削过程功率曲线图。

图3 数控车床工作过程典型功率曲线
由图3可以看出,车床系统空切阶段机械损耗功率Pmec包含两个部分:主传动系统机械损耗Pspindle和进给传动系统机械损耗Pfeed,即
Pmec=Pspindle+Pfeed
(8)
主轴启动后车床系统进入空转阶段,输入功率Pi即为空转功率Pidle。空转功率Pidle一部分消耗于待机功率P0,另一部分损失在车床的主传动系统中。Li等[9]将主传动系统机械损耗表达为主轴转速的一次函数:
Pspindle=k1n+b
(9)
式中,n为主轴转速,r/min;k1、b为主电机功率系数。
Li等[9]将式(9)应用于机床系统输入功率Pi建模中,使得模型精度有了较大的提升。Li等[6]通过实验证实按照主轴转速n的一次函数拟合机床主传动系统机械损耗,仍可以保证较高的精度。刘飞等[11]通过理论推导证实机床机械系统主传动环节的机械损耗大致可以分为两个部分:与角速度成正比的库仑摩擦损耗,与角速度的平方成正比的黏性摩擦损耗。库仑摩擦损耗又可以进一步分成两部分:与载荷无关的非载荷库仑摩擦损耗,与载荷相关的附加载荷功率损耗。即
Pspindle=Momω+Bmω2+Padd
(10)
式中,Mom为主传动系统等效摩擦力矩;Bm为主传动系统等效黏性阻尼系数;ω为主电机角速度。
对于空切阶段,主轴载荷为零,与之相关的附加载荷也为零。由此,空切阶段车床主传动系统机械损耗可表达为主轴转速n的二次函数:
Pspindle=a1n+b1n2
(11)
式中,a1、b1为车床主传动系统功率损耗系数。
车床系统空转功率
Pidle=P0+Pspindle=P0+a1n+b1n2
(12)
当进给系统启动之后,车床系统进入空切阶段。由图3可以看到车床系统输入功率Pi有小幅增加。这是因为车床进给系统开启之后,进给传动链上造成了机械损耗,但是该部分损耗所占输入功率Pi的比重较小。部分文献认为该部分功率损耗可以忽略不计,Li等[9]建立机床系统输入功率Pi的模型时,忽略了进给系统功率损耗。然而,He等[12]通过实验证实,车削过程中进给系统能量损耗超过车床系统能耗总量的5%,这证明进给系统机械损耗是不可忽略的。刘飞等[11]指出,对于进给系统有电机单独驱动的机床,其进给系统机械损耗与主传动系统机械损耗并无本质区别。因此,进给系统机械损耗为

(13)
式中,vf为进给速度,mm/min;a2、b2为进给传动系统功率损耗系数。
周丹等[10]指出,电机的电损功率PLe包含复杂的内容:铁芯损耗PFe,定/转子铜耗PCu以及杂散损耗Pfs。电机的电损功率PLe与其本身的工作状态、电机输出轴载荷密切相关。电损功率PLe由于其发生机理的复杂性而难于用切削参数来精确建模预测。而且,因其本身数值不大,在车床系统输入功率Pi中所占比例较小,在理论建模中通常忽略不计。但在实际回归建模中,由于电机处于机械系统传动链的源头,故电机的电损功率PLe可以由机械系统传动损耗二次拟合产生的常数项作一定程度的补偿。
由此,可以得出车床系统空切阶段功率为
Pair=P0+Pmec=P0+a1n+b1n2+a2nf+b2(nf)2
(14)
当车床系统进入稳定切削阶段,输入功率Pi一部分流向车床系统待机功率P0,一部分损耗在车床机械传动系统中发热与产生振动,一部分消耗在电机的铁芯、绕组中产生焦耳热,剩余部分则作为切削功率Pc转移到了工件和切屑中。
切削功率Pc既是机床系统的能耗中的“有功部分”,又在机床系统输入功率Pi中占据了较大比重,长期以来一直是输入功率Pi建模的焦点。传统上,学者们采用切削力Fc来评估机床的切削功率,即
Pc=Fcvc
(15)
式中,Fc为切削力。
获取切削力Fc的方法较多,Armarego等[13]采用指数型经验模型建立了Fc与工艺参数的大致关系,Oxley[14]通过对垂直车削模型的理论分析阐明了Fc与工艺参数之间较为准确的函数。近年来又发展起来应用神经网络预测Fc[15]等诸多新方法。Li等[6]结合刀具技术说明提出切削力系数形式的切削力计算方法:
Fc=kcAc
(16)
式中,kc为切削力系数;Ac为切削面面积。
该方法为Gutowski等[4]所提出的功率模型提供了理论支持,因此可得切削功率Pc的计算公式如下:
Pc=Fcvc=kcAcvc=kcηMRR
(17)
当车床系统进入稳定切削阶段,损耗在主传动系统中的附加载荷功率损耗Padd不再为零,而是与切削功率Pc相关的函数。刘飞等[16]指出附加载荷损耗功率Padd可用切削功率Pc的一次函数或者二次函数模拟。Diaz等[17]通过实验验证了机床系统输入功率Pi分离出空切功率Pair之后的剩余功率(切削功率Pc与附加载荷功率损耗Padd之和)与材料去除率ηMRR之间存在二次函数关系。由此证实了附加载荷功率损耗Padd的计算公式为
(18)
式中,a3、b3分别为车床主传动系统载荷功率损耗系数。
综合上述分析,可得数控车床系统在稳定运转阶段的输入功率Pi表达式如下:
Pi=P0+PLe+Pmec+Padd+Pc=
(19)

ESEC=Pi/ηMRR=[P0+PLe+a1n+b1n2+
a2nf+b2(nf)2]/ηMRR+k1+k2ηMRR
(20)
3实验验证
本实验以荆州荷花机床厂CK60数控车床为平台,进行中碳钢棒料的外圆车削实验,在完成车削工艺的过程中采集机床系统输入功率Pi数据,通过多元非线性回归分析计算上述模型待定参数。实验中采用YT15硬质合金直头半精车刀,在外形尺寸为φ50mm×400mm的45号钢棒料表面车削外圆。实验所需要测得的车削过程中数控车床系统输入功率Pi,由布置在车床系统电气柜总线上的WB9128-1型功率传感器采集。
CK60数控车床主轴转速分高低两个挡位,主传动系统对应两条传动链,本次实验采用高速挡进行。棒料装夹及切削如图4所示。WB9128-1功率传感器安装在机床电源总线上,功率信号输出选用数字模式。采样频率设定为20Hz,采集到的RS485信号经转换器直接输入PC机。PC机获取16进制数字量功率数据后,通过MATLAB软件进行分析计算。功率采集接线方式如图5所示。

图4 车削实验现场图图5 功率传感器接线示意图
为了不失偏颇地考察各个切削参数对输入功率Pi的影响,笔者将各车削参数分别分为3个不同水平(表1),以组合正交试验方案。
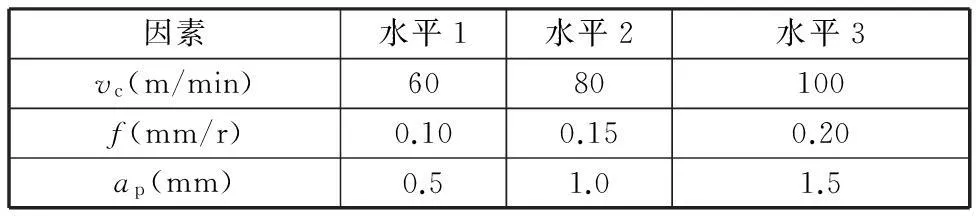
表1 参数水平表
在外圆车削过程中,随着实验的进行,棒料的直径d不断缩小。为了保证车削速度vc不变的实验条件,转速n将逐渐变大,其大小由下式决定:
(21)
因此,在编写数控车床NC代码时,车床系统的主轴转速n在每一组实验中都有所不同。表2为正交车削实验参数表。

表2 正交车削实验参数表
由车床系统的空转功率Pidle计算公式式(12),结合表2实验所采集的功率数据,可分离出主传动系统机械损耗Pspindle:
Pspindle=Pidle-P0
(22)
表3给出了主轴转速n与主传动系统机械损耗功率Pspindle的对应关系。

表3 主轴转速n与主传动系统机械损耗 P spindle的对应关系
现已知车床主传动系统机械损耗Pspindle与主轴转速n存在二次函数关系,通过对表3数据进行二次拟合即可得到主传动系统机械损耗Pspindle的计算公式:
Pspindle=1.506 56n+0.000 039n2+22.64(W)
(23)

图6 P spindle与n之间二次拟合关系
车床主传动系统机械损耗Pspindle与主轴转速n的二次拟合关系如图6所示。由图6可以看出,通过拟合得到的曲线二次趋势并不明显,因此,许多文献中将之表达为一次函数关系。本文从机械损耗的理论出发,力图建立更加精确的能量模型,因此仍采用二次型的主传动系统机械损耗模型。
同理,车床进给传动系统机械损耗Pfeed为空切功率Pair与空转功率Pidle之差。依据此功率关系,结合表2实验数据,即可分离得到车床进给传动系统机械损耗Pfeed与进给系统速度vf之间的对应关系,如表4所示。
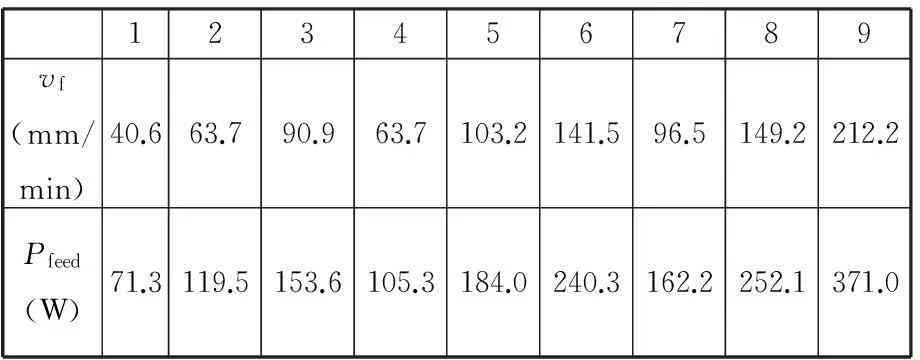
表4 进给速度 v f与进给传动系统
与车床主传动系统机械损耗Pspindle一样,已知进给系统机械损耗Pfeed与进给速度vf之间存在二次函数关系,通过二次拟合即可求得进给传动系统机械损耗Pfeed:
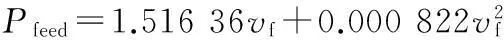
0.000 82(nf)2+10.93 (W)
(24)
综合上述分析,可求得数控车床系统在空切阶段的功率Pair的估算公式:
Pair=P0+Pmec=374.7+1.506 56n+0.000 039n2+
1.516 36nf+0.000 82(nf)2+33.57(W)
(25)
通过理论分析可知,主传动系统机械损耗Pspindle和进给传动系统机械损耗Pfeed仅与主轴转速n和进给速度vf二次相关,不应包含常数项。但是实测数据通过二次拟合的结果都显示出了大小不可忽略的常数项,空切功率Pair中包含的二次拟合的常数项之和甚至达到33.57W。这是由于以电机为动力源的传动链上的功率损耗不仅包含了传动系统的机械损耗,还应包含电机的电损功率PLe。电损功率PLe难于由切削参数直接建模得到,因而用传动系统整体能耗二次函数建模产生的常数项来作一定程度的补偿,以此矫正系统误差、提高模型精度。
当车床系统进入稳定切削阶段时,切削载荷不仅会消耗车床系统的切削功率Pc,还会造成主传动系统机械传动部分的附加载荷损耗Padd。在缺少专业设备直接测量车床系统切削功率Pc的准确数值的条件下,切削功率Pc与由其所引起的附加载荷功率损耗Padd难于分离。现已知附加载荷功率损耗Padd是切削功率Pc的二次函数,将切削功率Pc与附加载荷功率损耗Padd视为整体,即可将其表达为材料去除率ηMRR的二次函数。
通过实验数据分离出的车床系统切削功率Pc与附加载荷功率损耗Padd之和与对应的材料去除率ηMRR之间的对应关系如表5所示。经二次拟合即可得到切削功率Pc与附加载荷功率损耗Padd之和的计算公式:
(26)
其中,常数项19.16W是指由附加载荷引起的机床主电机电损功率补偿值,二次拟合关系如图7所示。

表5 切削功率P c和附加载荷功率损耗P add

图7 P c与P add之和与η MRR的二次拟合关系
(27)
则数控车床系统稳定切削阶段单位体积能耗模型为
ESEC=Pi/ηMRR=[427.43+1.506 56n+
0.000 039n2+1.516 36nf+0.000 82(nf)2]/ηMRR+
3.136 32+0.000 36ηMRR
(28)
4模型对比分析
按照上述分析方法,即可建模得到数控车床系统稳定切削阶段输入功率Pi的估算公式。与实测加工过程的功率数据进行对比分析,结果显示,该模型所预测的输入功率Pi具有较高的精度。
车床输入功率的实测值与模型预测值的对比结果如表6所示。经对比分析可以发现,本文提出的预测模型对数控车床系统稳定切削阶段的输入功率Pi的预测精度最高可达99.43%,平均精度也达到了98.59%。此外,该模型能较为准确地分辨出车床系统的待机功率P0、主传动系统机械损耗Pspindle、进给传动系统机械损耗Pfeed,以及切削功率Pc和由此引起的附加载荷功率损耗Padd。由于各能耗分支的独立性和数控车床运行状态的阶段性,本文提出的Pi模型不仅适用于车床系统稳定切削阶段输入功率的评估,同样适用于车床系统稳定的待机阶段、空转阶段和空切阶段。该模型理论基础健全,能量走向清晰,对预测机械加工全过程能量消耗、改进工艺过程、优化切削参数、监控车床系统工作状态具有很好的指导意义。

表6 模型精度分析
由本文实验采集的功率数据,根据Gutowski等[4]提出的模型,可以得出相应的输入功率Pi估算公式:
Pi=1299.96+5.188 86ηMRR(W)
(29)
Li等[9]在考虑了机床系统主传动系统机械损耗之后,提出了改进的机床系统输入功率Pi模型。结合本文实验采集的功率数据,经过多元线性回归可以得出Li等[9]提出的输入功率估算公式Pi如下:
Pi=382.38+1.771 45n+3.515 93ηMRR(W)
(30)
分析上述拟合公式式(29)、式(30)发现,Gutowski等[4]提出的模型仅是依据实验数据经数学拟合得到,不仅拟合误差大,而且根据拟合公式无法体现车床系统的任何参数特征。Li等[9]所提出的模型在Gutowski等[4]的模型基础上作了重大改进,预测精度大幅提高,且能够比较准确地体现车床系统在稳定切削阶段的能量流向,但是该模型忽略了进给系统的功率损耗与附加载荷功率损耗,且该模型仅适用于数控车床系统稳定切削阶段,对车床系统空转、空切功率的预测精度较低。
在表7中,模型1为式(27)拟合所得模型,模型2和模型3分别为式(29)、式(30)拟合所得模型。由表7可以看出,本文提出的改进型功率模型显示出更高的精确性,平均误差仅1.41%,低于文献[4]中的15.91%和文献[9]中的2.79%。而且在拟合优度和残差上,本文所提出的模型均显著优于模型2和模型3。
基于上述理论分析与实验对比,可知本文所提改进型数控车床系统输入功率Pi模型不仅在理论基础上清晰完整,而且预测精度有显著提高。

表7 预测模型误差对比
因此,在此改进型车床系统输入功率模型基础上,进一步发展可得到数控车床系统稳定切削阶段单位体积能耗SEC模型。精确的SEC模型将在以能耗为目标的切削参数优化中起到关键作用。
5结语
本文基于车床系统的能量守恒,结合Li等[9]总结的模型,提出了一种改进型数控车床系统输入功率Pi模型。该建模方法仅需采用简单的设备——功率传感器。通过分析不同状态下的数控车床系统输入功率,分离出机床系统各部分能量流向,并各自独立建模。将独立建模的各部分能耗汇聚起来,构成了车床系统输入功率Pi模型。该方法建立的机床系统输入功率Pi模型,不仅能根据切削参数快速、准确地预测数控车床系统功耗,而且从模型本身即可快速分离车床系统能量走向。由于各能量分支的功率模型彼此独立,使得该模型不仅适用于数控车床系统稳定切削阶段的能耗预测和车床系统能效评价,同时也适用于稳定的待机阶段、空转阶段、空切阶段,进而能够准确预测车床系统车削加工全过程的能量消耗。在此改进型输入功率Pi模型的基础上,本文进一步提出了数控车床系统稳定切削阶段单位体积能耗SEC模型,该模型对于优化切削参数、提高机床能量利用率具有重要意义。
参考文献:
[1]中华人民共和国国家统计局.中国统计年鉴2013[M].北京:中国统计出版社,2013.
[2]刘飞,王秋莲,刘高君.机械加工系统能量效率研究的内容体系及发展趋势[J].机械工程学报,2013,49(19):87-94.
LiuFei,WangQiulian,LiuGaojun.ContentArchitectureandFutureTrendsofEnergyEfficiencyResearchonMachiningSystems[J].ChineseJournalofMachineEngineering,2013,49(19):87-94.
[3]DietmairA,VerlA.EnergyConsumptionForecastingandOptimizationforToolMachines[J].Energy,2009(3):62-67.
[4]GutowskiT,DahmusJ,ThiriezA.ElectricalEnergyRequirementsforManufacturingProcesses[C]//13thCIRPInternationalConferenceonLifeCycleEngineering.Leuven,Belgium:CIRP,2006:560-564.
[5]AbeleE,SielaffT,SchifflerA,etal.AnalyzingEnergyConsumptionofMachineToolSpindleUnitsandIdentificationofPotentialforImprovementsofEfficiency[M]//GlocalizedSolutionsforSustainabilityinManufacturing.Berlin:Springer-Verlag,2011.
[6]LiW,KaraS.AnEmpiricalModelforPredictingEnergyConsumptionofManufacturingProcesses:aCaseofTurningProcess[J].JournalofEngineeringManufacture,2011,225(9):1636-1646.
[7]LiW,ZeinA,KaraS,etal.AnInvestigationintoFixedEnergyConsumptionofMachineTools[M]//GlocalizedSolutionsforSustainabilityinManufacturing.Berlin:Springer-Verlag,2011.
[8]陈宁.机床加工能耗及碳排放量定量分析方法研究[D].哈尔滨: 哈尔滨工业大学,2012.
[9]LiL,YanJH,XingZW.EnergyRequirementsEvaluationofMillingMachinesBasedonThermalEquilibriumandEmpiricalModelling[J].JournalofCleanerProduction,2013,52(1):113-121.
[10]周丹,刘光复,何平.数控机床能量设计因子提取方法研究[J].中国机械工程,2011,22(3):351-355.
ZhouDan,LiuGuangfu,HePing.StudyonExtractingMethodofEnergyDesignFactorsforNCMachines[J].ChinaMechanicalEngineering,2011,22(3):351-355.
[11]刘飞,徐宗俊,但斌,等.机械加工系统能量特性及其应用[M].北京:机械工业出版社,1996.
[12]HeY,LiuF,WuT,etal.AnalysisandEstimationofEnergyConsumptionforNumericalControlMachining[J].JournalofEngineeringManufacture,2012,226(2):255-267.
[13]ArmaregoEJA,OstafievD,WongSWY,etal.AnAppraisalofEmpiricalModelingandProprietarySoftwareDatabasesforPerformancePredictionofMachiningOperations[J].MachiningScienceandTechnology,2000,4(3):479-510.
[14]OxleyPLB.DevelopmentandApplicationofaPredictiveMachiningTheory[J].MachiningScienceandTechnology,1998,2(2):165-189.
[15]SharmaVS,DhimanS,SehgalR,etal.EstimationofCuttingForcesandSurfaceRoughnessforHardTurningUsingNeuralNetworks[J].JournalofIntelligentManufacturing,2008,19(4):473-483.
[16]刘飞,刘霜.机床服役过程机电主传动系统的时段能量模型[J].机械工程学报,2012,48(21):132-140.
LiuFei,LiuShuang.Multi-periodEnergyModelof

Electro-mechanicalMainDrivingSystemDuringtheServiceProcessofMachineTools[J].ChineseJournalofMachineEngineering,2012,48(21):132-140.
[17]DiazN,RedelsheimerE,DornfeldD.EnergyConsumptionCharacterizationandReductionStrategiesforMillingMachineToolUse[M]//GlocalizedSolutionsforSustainabilityinManufacturing.Berlin:Springer-Verlag,2011.
(编辑卢湘帆)

