四足机器人改进型对角小跑步态研究
四足机器人改进型对角小跑步态研究
常青韩宝玲罗庆生
北京理工大学,北京,100081
摘要:传统的四足机器人对角小跑步态一般在机体坐标系中进行规划,在实际应用中存在着摆动腿无法同时着地、机体翻转无法有效抑制等问题,这些都降低了机器人运动的稳定性和精确性。针对以上问题,提出了一种在世界坐标系下规划的改进型对角小跑步态方法,该方法通过浮动机体运动学对摆动相进行规划,在足端的雅可比矩阵中引入机体姿态相关项,从而保证了摆动腿能同时着地,同时在支撑相和摆动相之间增加了四腿同时着地的调整相,对机器人机体位姿进行调整。对比仿真和样机试验结果表明:与传统方法相比,所提方法能够使摆动腿同时着地并能连续调整机体位姿,使机器人获得更好的运动稳定性和更高的位移控制精度。
关键词:四足机器人;改进型对角小跑步态;浮动机体运动学;调整相
中图分类号:TP242.6
收稿日期:2015-03-31
基金项目:国家高技术研究发展计划(863计划)资助项目(2011AA041002);总装备部预研基金资助项目(104060103)
作者简介:常青,男,1987年生。北京理工大学机械与车辆学院博士研究生。主要研究方向为仿生机器人设计与控制算法。出版专著1部,发表论文6篇。韩宝玲,女,1956年生。北京理工大学机械与车辆学院教授、博士研究生导师。罗庆生,男,1955年生。北京理工大学机电学院教授、博士研究生导师。
StudyonanImprovedTrotGaitforQuadrupedRobot
ChangQingHanBaolingLuoQingsheng
BeijingInstituteofTechnology,Beijing,100081
Abstract:The classical trot gait for quadruped robot was planned in the body coordinate of robot, and there exist some problems which might decrease the stability and accuracy of the locomotion in practical applications.For example, the swing legs could not land the ground simultaneously,and the rolling-over of the body could not be suppressed effectively. To overcome the problems,an improved trot gait for quadruped robot which was considered in the world coordinate was proposed herein.The swing phase was planned via kinematics with floating base, and the term related to the body’s position and attitude was introduced in the foot’s Jacobian matrix to ensure the swing legs could land the ground simultaneously. The adjustment phase was introduced between the support phase and swing phase when the four legs got in touch with ground. The body’ posture might be adjusted in the adjustment phase. Finally, the results of simulation and prototype experiments show that, the proposed method can improve the stability and accuracy of the robot’s locomotion.
Keywords:quadrupedrobot;improvedtrotgait;kinematicswithfloatingbase;adjustmentphase
0引言
仿生机器人一直是机器人领域的研究热点。四足机器人因具有较强的运动稳定性和较低的机构复杂度,吸引了国内外众多学者的关注[1-2]。近年来,随着液压伺服技术的发展,采用液压驱动的四足机器人开始出现,在极大提高四足机器人运动性能的同时,也对机器人的控制水平提出了更高的要求。如何使四足机器人在高速运动过程中保持机体稳定也成了各国学者必须考虑的问题。
在液压四足机器人中比较有代表性的是美国波士顿动力公司的“Bigdog”系列机器人[3-4]和意大利理工大学的HyQ机器人[5]。其中“Bigdog”系列机器人具有强大的运动平衡能力,能根据机体运动情况实时调整运动策略以保持机体稳定,但关于其控制算法的报道较少[6]。国内液压四足机器人研究虽然开展较晚,但却取得了不小的进展[7-12]。对角小跑步态是四足机器人最为常用的动态步态,文献[7-8]对此进行了研究,并提出了摆线方程的足端轨迹规划方法。此后王立鹏等[9]在文献[8]的基础上对足端轨迹进行了优化,提出了零冲击的足端轨迹规划方法。文献[10]提出了一种基于参数化坐标变换矩阵的方法,将对角小跑运动由直线运动进一步扩展到了转向和斜向运动中。在现有对角小跑步态规划中,步态的负载因子都设为0.5,即支撑相和摆动相各占运动周期的一半,同一时刻有两条腿处于支撑相。由于机体重心投影无法始终处于支撑腿足端连线上,故机器人机体将沿这条连线产生一定的翻转,而摆动相的运动规划在机体坐标系中进行,无法考虑机体翻转的影响,这就导致摆动腿不能同时着地,先着地的腿继续运动对机体产生较大冲击。步幅越大,周期越长,这种冲击对机体姿态的影响就越明显。文献[11]试图通过对角小跑起步姿态的调整来削弱翻转力矩的不利影响,但这种方法只能在运动开始阶段对翻转起到一定的抑制作用,而后续运动中产生的翻转无法得到有效缓解。为此本文提出了一种改进型的对角小跑步态,使摆动腿同时着地,并在调整相中对机体位姿进行实时调整,以提高机器人运动的稳定性和精确性。
1支撑相运动规划
本文所研究的四足机器人如图1所示,每条腿都有3个关节,共有12关节,全部采用液压缸进行驱动。采用D-H法建立图2所示的机器人运动学模型,其中坐标系{W}代表世界坐标系,坐标系{B}建立在机体质心处,代表机体坐标系。L1、L2、L3和L4分别代表机器人的四条腿,因为四条腿上坐标系的建立方法一致,故以L2为例进行说明。坐标系{0}建立在侧摆关节中心处,坐标系{1}、{2}和{3}表示侧摆、大腿和小腿的杆件坐标系,分别建立在侧摆关节中心、髋关节中心及膝关节中心处。θ21、θ22和θ23分别为L2侧摆关节、髋关节和膝关节的关节角度值,l1、l2和l3为侧摆、大腿及小腿的长度。e2为L2足端位移向量。

图1 液压四足机器人

图2 四足机器人运动学模型
根据图2所示的运动学模型,采用D-H法可求得L2足端在坐标系{0}的坐标:
(1)
式中,si=sinθ2i,ci=cosθ2i,i=1,2,3。
对式(1)进行求解可以得到L2的各关节角:
(2)
(3)
当L2处于支撑相时,其足端在世界坐标系中没有移动,如果此时机体质心在世界坐标系{W}中各轴所对应的位移分别为bx、by和bz,则px、py和pz可以用下式表示:
(4)
其中,WR0为坐标系{0}到世界坐标系{W}的旋转变换矩阵。根据式(1)~式(4),就可求出处于支撑相的腿部关节角。
2利用浮动机体运动学对摆动相进行规划
2.1浮动机体运动学
与基座固定的机器臂不同,足式机器人在运动过程中并没有杆件固定在世界坐标系中,因而可以看作是浮动机体系统。在世界坐标系中,足式机器人的完全构型q可以由下式决定:
(5)
式中,θLi=[θi1θi2θi3]T,表示四足机器人腿Li的关节角;xB为6×1向量,表示机器人机体相对于世界坐标系的位置和姿态。

(6)
(7)

式(7)中∂eLi/∂xB又可以用下式表示[12]:
(8)
式中,I为3×3的单位矩阵;RB为机器人机体相对于世界坐标系的旋转矩阵;BeLi为第i条腿足端在机体坐标系中坐标;RB×BeLi表示矩阵RB中的列向量分别与BeLi叉乘。
将式(6)和式(7)进行整理可得
(9)
在已知处于摆动相的Li足端的运动速度和机体运动状态下,可以利用式(9)求解摆动腿关节角速度。
2.2摆动相的足端轨迹规划
为了保证足端在着地时的速度尽量为0,从而减少地面的冲击,采用文献[10]所提出的足端运动轨迹,如下所示:
(10)
式中,ex、ey、ez为摆动腿足端在世界坐标系中的位移;ex0、ey0、ez0为摆动相开始时足端的位移;Tb为摆动相的时长;S为足端在摆动相中沿x轴方向移动的距离;H为抬腿高度;D为足端在摆动相中沿y轴方向移动的距离。
将此运动轨迹进行微分就得到了足端在世界坐标系中的速度方程,如下所示:
(11)
3调整相运动规划方法
文献[12]通过分析认为:当四足机器人支撑腿超过3条,并且接触点不在同一条直线上时,机体位姿可以由支撑腿的构型进行调整。为了对机体的姿态进行调整,本文在支撑相和摆动相之间增加了四腿同时着地的调整相,具有调整相的对角小跑步态的时序如图3所示。其中白色框代表腿部处于摆动相,黑色框代表腿部处于支撑相,而灰色框则代表腿部处于调整相。
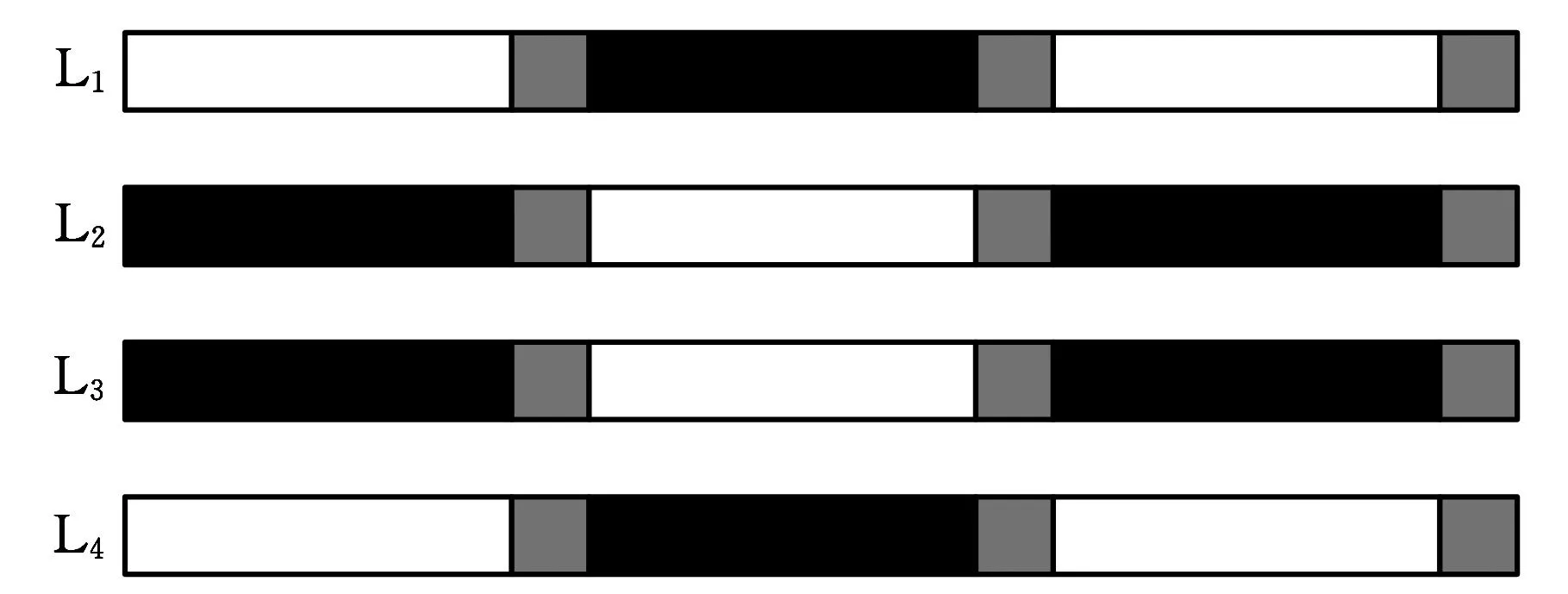
图3 改进型对角步态的时序图
如果将L1、L2、L3和L4一同考虑,将式(6)和式(7)进行整理可得
(12)

(13)

(14)
式中,bxd、byd、bzd分别为机体在世界坐标系{W}中各轴位移的期望值;αd、βd、γd为机体横滚角、俯仰角和航向角的期望值;λ<0,为负反馈增益。
4仿真分析与样机试验
4.1仿真条件设置
以图1中液压四足机器人的尺寸和质量等参数为基础,在Webots机器人仿真软件中建立了简化的仿真模型,并在其上添加了陀螺仪、加速度计、足端力传感器、关节角度编码器等传感器,如图4所示。为了对所提出的算法的可行性和有效性进行验证,进行两组仿真对比实验。其中第1组仿真采用文献[6]中所提出的零冲击的足端轨迹规划方法,仿真中机器人以200mm/s的速度沿直线运动,一个摆动相和支撑相的时间均为0.25s,摆动相步长为100mm,抬腿高度为80mm。第2组仿真采用本文所提出的改进型对角小跑步态,仿真中机器人同样以200mm/s的速度沿直线运动,摆动相时间为0.2s,支撑相时间为0.2s,调整相的时间为0.05s,摆动相步长为100mm,抬腿高度为80mm。由于是直线运动,byd、bzd、αd、βd、γd的值均为0,bxd为200t,其中t代表运动时间,负反馈增益λ设为-100。两组仿真的总时长均为5s,各包含10个运动周期,仿真时间间隔为0.005s,其他仿真设置也完全一致。
图4 Webots软件中的仿真模型
4.2仿真结果分析
机器人机体的姿态角尤其是横滚角和俯仰角的变化最能反映机器人的运动是否稳定。从图5可以看出,使用本文所提方法的第2组仿真中姿态角的变化更小,从而证明本文所提方法能够有效提高机器人运动的稳定性。同时也可以看出在第2组仿真中,当机器人腿部进入调整相时(如2.45~2.5s),各姿态角都有较明显的调整,当机器人腿部不在调整相时姿态角则开始增大。由此可见,调整相的不断调整使得机器人的姿态角在较小的范围内变化。

图5 仿真中机器人机体姿态角
在两种运动规划方法中,L2和L3始终处于同一种相位中,故以L2和L3为例分析两组仿真中机器人足端所受冲击的情况。从图6中可以看出,在第1组仿真中,L2和L3在支撑相中的受力不均,随着时间的变化这种受力不均现象更为明显,而支撑足受力不均使机体产生的翻转力矩是影响机器人稳定性的重要因素。同时可以看出L2和L3的着地时间也与规划时间(0.25s)的差别越来越大,这是由于规划中并未考虑机体翻转对运动影响。L3先于规划进入支撑相,与L1和L4形成三腿支撑,而L2则晚于规划进入支撑相,此时L1和L4已进入摆动相,需要抬起,因而L2所受的冲击较大。而在第2组仿真中L2和L3则基本上能保持在相同相位中,与地面的冲击较为均匀,产生的机体翻转力矩较小。尤其是从摆动相进入调整相的过程中能够同时着地形成四腿支撑,这正是调整相进行调整的前提条件。

(a)第1组仿真中L 2受到的足端冲击力

(b)第1组仿真中L 3受到的足端冲击力
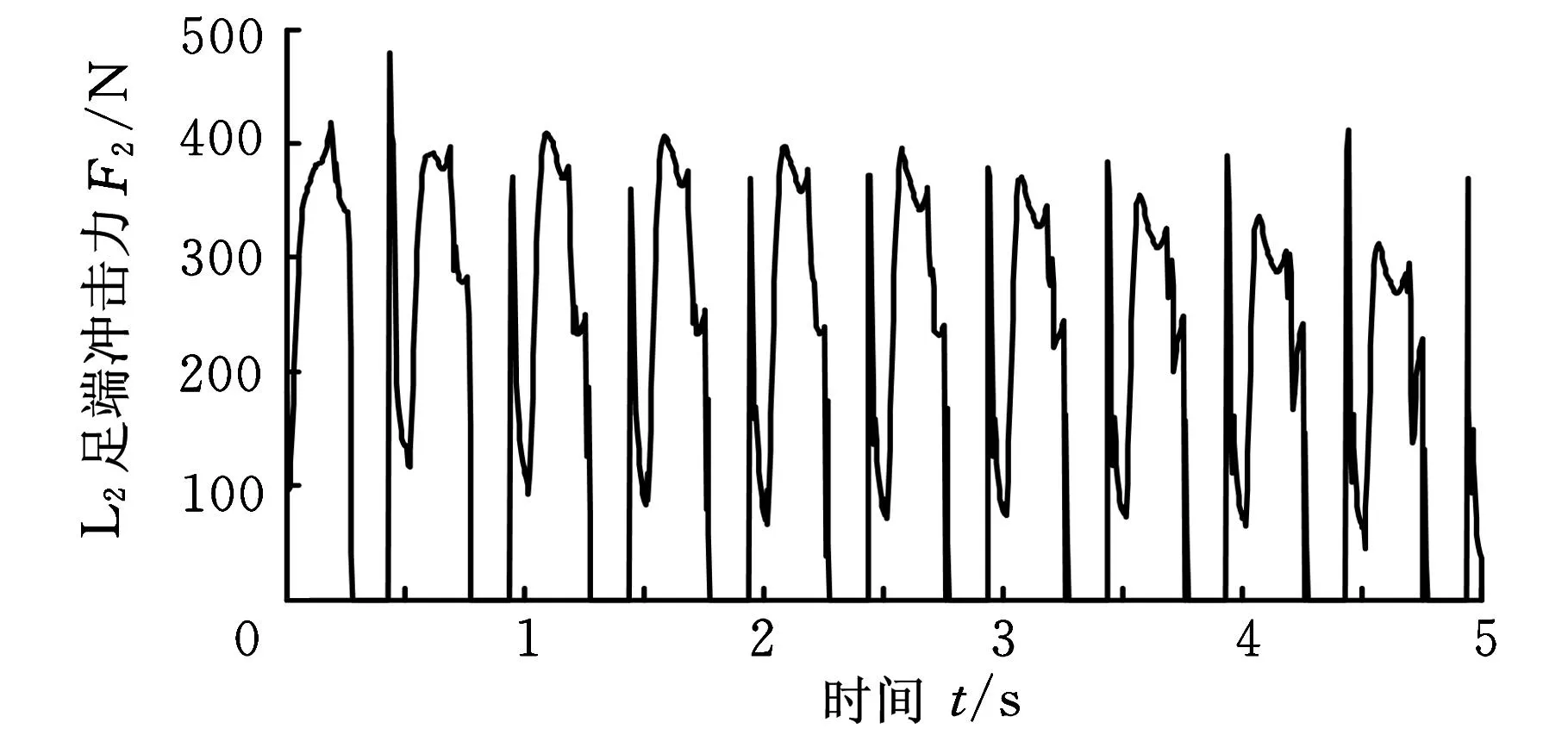
(c)第2组仿真中L 2受到的足端冲击力

(d)第2组仿真中L 3受到的足端冲击力 图6 两组仿真中L 2和L 3受到的足端冲击力

图7 两组仿真中机体位移
图7所示为两组仿真中机体位移变化情况。在第1组仿真中的相位转换阶段由于机器人姿态变化较大,机器人在各方向位移都产生了较大的波动。尤其是机器人前进的x方向,这种波动更为明显。在第2组仿真中,由于机器人机体运动平稳,所受地面冲击力较小,机体位移变化较为平稳。在两组仿真的规划中,机器人步长均为100mm,均以200mm/s的速度沿直线运动5s,x方向的位移都应为1m。而第1组仿真结束后,机器人在x方向的位移为617.9mm,产生了38.2%的误差;第2组仿真结束后,机器人在x方向的位移为1046.3mm,误差仅为4.6%。可见由于本文所提方法在世界坐标系中进行规划,并且在运动过程中机体较为平稳,因而能够对机器人的实际位移进行更为精确的控制。
4.3样机试验
为了对本文提出的步态规划算法进行进一步验证,在图2所示的液压四足机器人上进行了试验验证。考虑到样机的实际情况,将摆动相、支撑相、调整相的时间分别调整为0.4s、0.4s和0.1s,运动步长和抬腿高度均调整为50mm,试验过程如图8所示。其中图8c、图8d中,机器人处于调整相,对机体姿态进行调整。从图中可以看出使用本文所提方法,机器人实现了较为平稳的直线行走,从而证明所提方法的可行性。

(a)t=0s (b)t=0.2s(c)t=0.4s

(d)t=0.45s (e)t=0.5s(f)t=0.7s

(g)t=0.9s(h)t=1s 图8 四足液压机器人物理样机试验
5结论
为了提高四足机器人对角小跑步态运动的稳定性和精确性,本文提出了一种改进型对角小跑步态规划方法,并通过仿真分析和样机试验证明了所提方法的可行性和有效性。和传统规划方法相比,本文所提方法具有以下创新点:
(1)采用浮动机体运动学对摆动相进行规划,考虑了机体姿态变化对于足端轨迹的影响,从而保证摆动腿能够同时着地,使足端所受冲击力更为均匀。
(2)在支撑相和摆动相之间增加了四腿同时着地的调整相,根据实际运动情况对机器人机体姿态进行调整,提高了机器人运动的稳定性。
(3)步态规划在世界坐标系中进行,提高了机器人运动位移的控制精度。
在本文中,调整相姿态调整算法还较为粗糙,在后续研究中,将对调整相中机体位姿参数提出更为精细的调整算法,用所提算法解决对角小跑的转向和斜向运动以及机体受冲击后的平衡恢复问题。
参考文献:
[1]谭民,王硕.机器人技术研究进展[J].自动化学报,2013,39(7):963-972.
TanMin,WangShuo.ResearchProgressonRobotics[J].ActaAutomaticSinica,2013,39(7):963-972.
[2]雷静桃,俞煌颖,王峰.四足机器人对角小跑步态动态稳定步行足端非连续约束及动力学建模[J].中国机械工程,2015,26(5):592-597.
LeiJingtao,YuHuangying,WangFeng.AnalysisonNon-continuousConstraintsandDynamicsModelingofQuadrupedRobotDynamicallyStableWalkingwithTrotGait[J].ChinaMechanicalEngineering,2015,26 (5):592-597.
[3]RaibertM,BlankespoorK,NelsonG.BigDog,theRough-terrainQuadrupedRobot[C]//17thWorldCongress,InternationalFederationofAutomationControl.COEX,2008:1822-1825.
[4]WoodenD,MalchanoM,BlankespoorK,etal.AutonomousNavigationforBigDog[C]//2010IEEEInternationalConferenceonRoboticsandAutomation(ICRA).Anchorage:IEEE,2010:4736-4741.
[5]SeminiC.HyQ-DesignandDevelopmentofaHydraulicallyActuatedQuadrupedRobot[D].Genova:ItalianInstituteofTechnology,2010.
[6]丁良宏,王润孝,冯华山,等.浅析Big-Dog四足机器人[J].中国机械工程,2012,23(5):505-514.
DingLianghong,WangRunxiao,FengHuashan,etal.BriefAnalysisofaBig-DogQuadrupedRobot[J].ChinaMechanicalEngineering,2012,23(5):505-514.
[7]李贻斌,李斌,荣学文,等.液压驱动四足仿生机器人的结构设计和步态规划[J].山东大学学报(工学版),2011,41(5):32-36.
LiYibin,LiBin,RongXuewen,etal.MechanicalDesignandGaitPlanningofaHydraulicallyActuatedQuadrupedBionicRobot[J].JournalofShandongUniversity(EngineeringEdition),2011,41(5):32-36.
[8]CaiRunbin,ChenYangzhen,HouWenqi,etal.TrottingGaitofaQuadrupedRobotBasedontheTime-poseControlMethod[J].InternationalJournalofAdvancedRoboticSystems,2013,10(148):1-7.
[9]王立鹏,王军政,汪首坤,等.基于足端轨迹规划算法的液压四足机器人步态控制策[J].机械工程学报,2013,19(1):39-44.
WangLipeng,WangJunzheng,WangShoukun,etal.StrategyofFootTrajectoryGenerationforHydraulicRobotsGaitPlanning[J].JournalofMechanicalEngineering,2013,19(1):39-44.
[10]常青,韩宝玲,罗庆生.四足机器人转向与斜向运动规划理论和方法研究[J].北京理工大学学报(自然科学中文版),2015,35(5):477-480.
ChangQing,HanBaoling,LuoQingsheng.SteeringandObliqueMovementPlanningMethodforQuadrupedRobots[J].TransactionsofBeijingInstituteofTechnology,2015,35(5):477-480.
[11]何冬青,马培荪,曹曦,等.四足机器人对角小跑起步姿态对稳定步行的影响[J].机器人,2004,26(6):529-532.
HeDongqing,MaPeisun,CaoXi,etal.ImpactofInitialStanceofQuadrupedTrottingonWalkingStability[J].Robot,2004,26(6):529-532.
[12]HutterM,SommerH,GehringC,etal.QuadrupedalLocomotionUsingHierarchicalOperationalSpaceControl[J].TheInternationalJournalofRoboticsResearch,2014,33(8):1047-1062.
(编辑袁兴玲)

