二维振动铣削切削厚度及刀尖轨迹数值仿真

二维振动铣削切削厚度及刀尖轨迹数值仿真

李东明田野

大连交通大学，大连，116028

摘要：通过分析二维振动铣削条件下刀尖运动轨迹特点，利用椭圆方程与旋转矩阵建立了描述刀尖运动轨迹最大轮廓的数学模型，在刀具同一转角下，运用距离间计算公式求得任意转角下的切削厚度值。通过对不同加工参数下刀尖轨迹数值仿真分析，获得了实现理想刀尖轨迹和切削厚度曲线的条件，从而为二维振动铣削的理论研究打下基础。

关键词：振动铣削；切削厚度；刀尖轨迹；数值仿真

中图分类号：TH161

收稿日期：2014-11-20

基金项目：辽宁省教育厅科学研究项目(L2014178)；浙江省零件轧制成形技术研究重点实验室开放基金资助项目

作者简介：李东明，男，1971年生。大连交通大学机械工程学院教授、博士。主要研究方向为传感器与测试技术、精密加工技术。田野，女，1989年生。大连交通大学机械工程学院硕士研究生。

NumericalSimulationofChipThicknessandToolTipPathinTwoDimensionalVibrationMilling

LiDongmingTianYe

DalianJiaotongUniversity,Dalian,Liaoning,116028

Abstract:Through the analyses of the characteristics of tool tip path in two dimensional vibration milling, a mathematical model of maximum contour line of tool path was built by using elliptic equation and rotation matrix.In the same tool angle,chip thickness could be calculated by using the distance formula. The tool tip paths of two dimensional vibration milling with different vibration parameters were simulated and analyzed.According to the results,the conditions of realizing the ideal tool path and chip thickness curve were summarized,which provides a good basis of the theory research in two dimensional vibration milling.

Keywords:vibrationmilling；chipthickness；tooltippath；numericalsimulation

0引言

振动加工就是在传统的切削加工基础上对工件或刀具施加一定频率的振动以改变加工模式，达到减小切削力[1]、降低表面粗糙度[2]、切屑处理容易[3-4]、减少刀具磨损[5-6]等良好的加工效果。二维振动切削的切削力比一维振动切削的切削力更小[7]，表面粗糙度值更小[8]，其良好的加工效果受到了各国学者的广泛关注。

目前，振动加工技术已经在车削、钻削等领域获得了大量的研究成果[9-10]，对振动铣削技术的研究成为振动加工的研究热点。在一维振动铣削方面，沈学会[11]进行了较系统的理论研究，从运动学方面分析了一维振动铣削的加工机理，并通过实验得出工件切削表面质量提高、刀具磨损减小等加工效果。在二维振动铣削方面，Chern等[12]利用压电陶瓷微驱动二维振动工作台进行了振动铣削的实验研究，实验研究表明:振动辅助微铣削可以改善加工沟槽的尺寸精度，降低切削表面粗糙度和延长刀具寿命。丁辉[13]从理论上对二维振动铣削的动力学过程进行了分析，并通过实验得出二维振动铣削的加工效果优于一维振动铣削的结论，但在切削厚度的计算方面，他没有给出具体的解析函数公式，在刀尖轨迹的分析中也没有给出获得最优理想刀尖轨迹的参数选择。因此，本文将针对这两点，从解析函数角度计算切削厚度，并依据二维振动铣削切削厚度变化的特点，对加工参数进行优化，以此求得理想的刀尖轨迹和切削厚度曲线，进而提高工件的加工效果。

1切削厚度数值仿真

1.1切削厚度形成过程分析

图1　Tlusty等 [14]的铣削厚度计算模型

目前，普遍应用的铣削厚度计算模型是由Tlusty等[14]提出的，假设刀具轨迹为圆，依据刀具的旋转过程，刀具的切削厚度近似为h=ftsinθ，ft为刀具的每齿进给量，θ为刀具的旋转角度，如图1所示。但是在二维振动铣削中，刀尖轨迹不再是类似圆的形状，而是随着刀具的旋转和振动的影响，呈现螺旋状，图2为两齿铣刀在二维振动铣削加工中刀尖轨迹仿真图，图中A点为前一刀尖轨迹上的点，B为后一刀尖轨迹上的点。

分析其运动过程可知，一次走刀过程中后一刀齿切削轨迹进入前一刀齿切削范围内时，对工件同一位置表面进行了第二次铣削；后一刀齿的刀尖位于前一刀齿的切削轨迹内时不产生切屑，切削厚度为零；后一刀齿的刀尖位于前一刀齿的切削轨迹外时产生切屑，切削厚度为同一刀具转角下切削刃与最大轮廓间交点的距离，即为图中A、B点间的距离。

因此，为求出二维振动铣削的切削厚度，只需求前后两切削轨迹的最大轮廓方程，然后计算出同一刀具转角下两最大轮廓上点的坐标，这两交点间的距离即为当前刀具转角下切削厚度数值。

1.2切削厚度计算

观察此最大轮廓曲线的变化规律，可近似地将其看作由若干个半椭圆接续而成。首先通过椭圆公式和刀具运动参数求得起始位置处半椭圆方程，然后通过一定的角度旋转可求得任意处的半椭圆方程，将所有刀具旋转半周期内的椭圆都求出后，就可确定最大轮廓上各点坐标，从而求得切削厚度值。具体计算过程如下：

(1)为求得椭圆方程，先求每两个半椭圆间的交点坐标。由于刀具的旋转角度、振动频率和振幅都呈周期性变化，从而椭圆间交点的坐标也呈现周期性，其变化周期为刀齿的旋转周期T，根据刀具的旋转规律和切削轨迹的特征，形成每一个交点的时间为

tn=t1+T(n-1)/k

(1)

式中，n=1,2,…为每一个交点的时间;k为切削轨迹中椭圆的个数。

则第n个交点的坐标(xn,yn)为

(2)

式中，vf为刀尖的进给速度；ω为刀具旋转角速度。

(3)

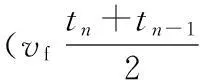
用同样的方法可以求得任意刀尖轨迹的最大轮廓点的坐标。整个计算程序的流程图见图3。

图3　振动铣削切削厚度计算流程图

通过以上算法求得相邻两切削轨迹的最大轮廓上点的坐标，在刀具同一旋转角度下，通过求两点间距离公式就可得到任意转角下的切削厚度，其仿真结果如图4所示。

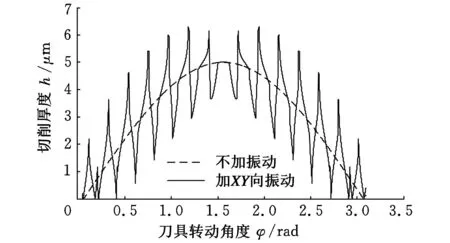
图4　二维振动铣削与传统铣削切削厚度

由图4可以看出，切削厚度变化曲线不再是一条规则的曲线，而是一条随着振动频率和幅值的变化而呈现起伏振荡的曲线，振荡的幅度由振动幅值控制，振荡变化的次数由振动频率决定。在初始阶段刀具切入工件和切出工件时，切削厚度迅速超过了最小切削厚度，对工件进行去除材料加工，减小了刀具与工件间的摩擦，对抑制毛刺的产生和延长刀具寿命起到了很大的作用。在刀具切入、切出阶段还出现了切削厚度为零的情况，此时，后一刀齿的切削刃在前一刀齿的切削轨迹内，不形成切屑，由此判断二维振动铣削是一个断续的切削过程，在一定的周期范围内，刀具与工件间歇性的接触和分离有利于切削液的进入，对于提高工件的加工表面质量有很大作用。

2刀尖轨迹数值仿真

加工参数的选择不同，所形成的刀尖运动轨迹也不同，其结果影响切削厚度变化，对工件的加工效果产生很大影响。为获得理想加工效果的螺旋状刀尖轨迹，本文选取振动频率、振幅、每齿进给量和主轴转速4个因素，分析其对刀尖轨迹的影响。假设每齿进给量都为2μm，表1为正交仿真参数表，其中λ为振动频率与主轴回转频率的比值。通过MATLAB仿真出铣刀刀尖轨迹，探索最优刀尖轨迹的参数选择。

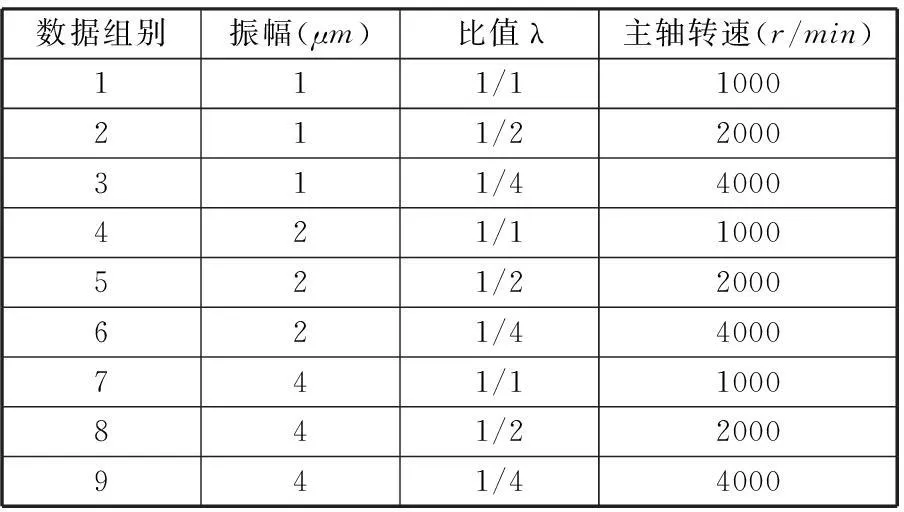
表1　正交仿真数据表

依据仿真数据，得出不同参数变化下的刀尖切削轨迹仿真图，如图5～图7所示(其中虚线、实线分别表示前后两刀齿的切削轨迹)。仿真分析结果表明，1～3组中都没有出现螺旋状刀尖轨迹(图5)；4～6组中，第4组出现螺旋状刀尖轨迹(图6a)，第5组刚好要出现螺旋状刀尖轨迹(图6b)，第6组没有出现螺旋状刀尖轨迹(图6c)；7～9组中，第7、8组出现明显的螺旋状刀尖轨迹(图7a、图7b)，第9组没有出现螺旋状刀尖轨迹(图7c)。

(a) 主轴转速为(b) 主轴转速为 1000r/min 2000r/min

(c)主轴转速为4000r/min

(a) 主轴转速为(b) 主轴转速为 1000r/min 2000r/min

(c)主轴转速为4000r/min

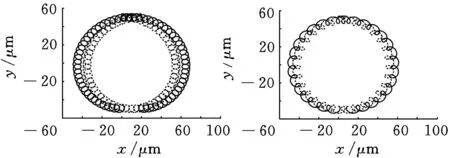
(a) 主轴转速为(b) 主轴转速为 1000r/min 2000r/min

(c)主轴转速为4000r/min

3实验验证

综合分析表明，振动幅值小于每齿进给量时都没有出现螺旋状的刀尖轨迹，而随着振动幅值与每齿进给量的比值越来越大，刀尖螺旋状运动轨迹越明显。当振动幅值一定时，随着振动频率与主轴回转频率比值的减小，螺旋状刀尖轨迹逐渐消失；当振动振动频率与主轴回转频率比值近似为1时，刀具旋转一周刀尖的螺旋状轨迹次数增多，如图7a所示，这种加工效果会使加工效率降低，并不是理想的刀尖运动轨迹，图7b(第8组)数据为理想的刀尖运动轨迹仿真图。根据第8组仿真数据，利用本文中切削厚度计算方法得出其切削厚度仿真图，结果同图4中加X、Y向振动的切削厚度曲线形状相似，此曲线即为理想的切削厚度曲线。基于以上分析，获得理想螺旋状刀尖运动轨迹和切削厚度曲线的条件为：振动幅值与每齿进给量的比值应大于等于2，但其比值不宜过大，否则影响加工效率；同时振动频率与主轴回转频率的比值应近似于1/2。

为了验证仿真分析的准确性，对Al6061进行二维振动铣削表面粗糙度实验。利用XY25XS压电陶瓷装置设计二维振动工作台，工件固定于振动工作台上，两齿硬质合金端铣刀固定于空气轴承主轴上，刀杆直径为0.5mm，螺旋角为30°，利用三维表面形貌轮廓仪(Zygo5000)测量切削表面粗糙度[15]。实验中振动频率为2000Hz，每齿进给量为2μm，主轴转速分别为4000r/min、7000r/min、10 000r/min，实验结果分析如图8所示。

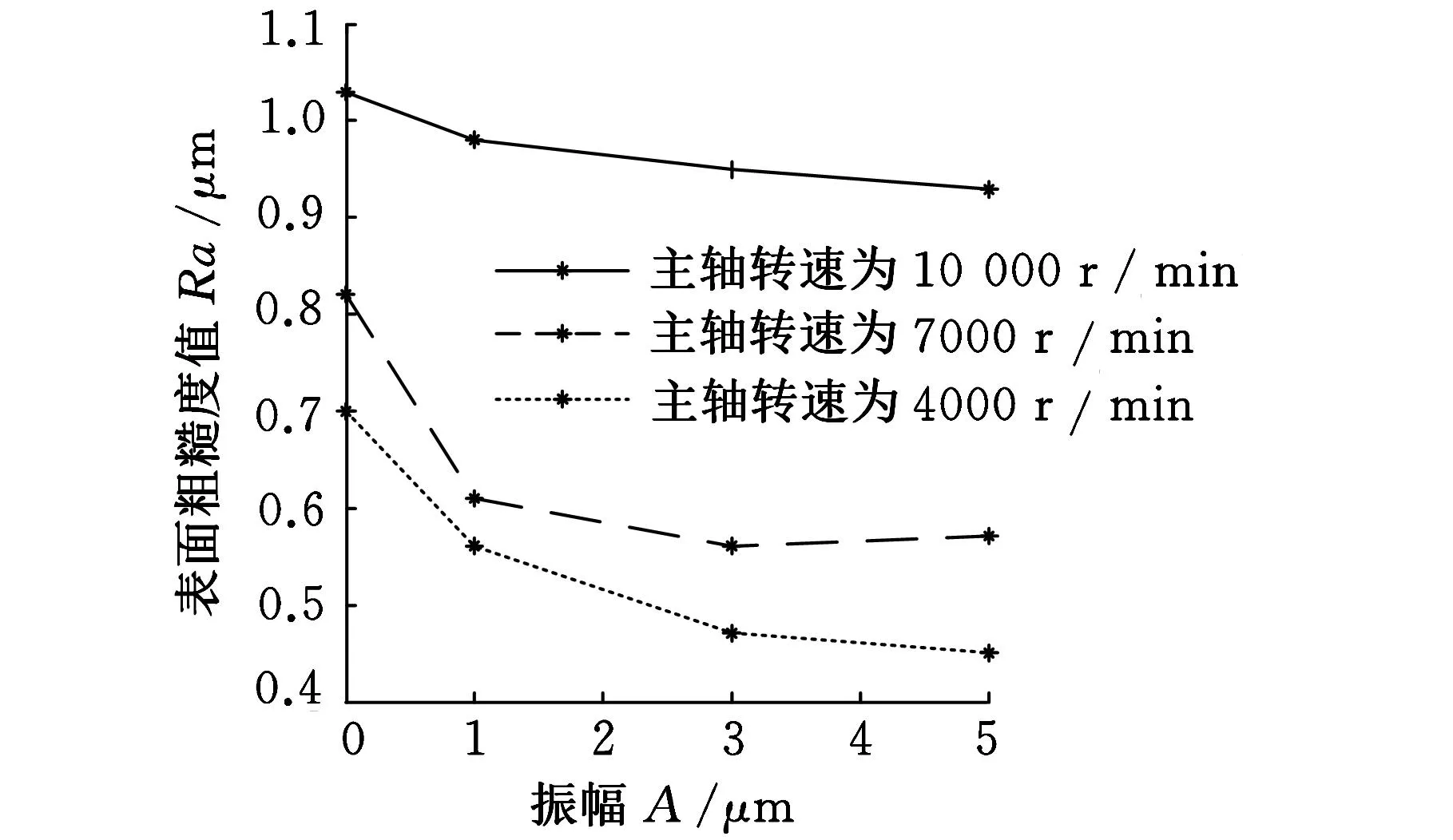
图8　表面粗糙度对比图

分析图8可知，二维振动铣削与普通铣削相比，粗糙度值明显减小，且主轴转速与振动频率的比值越接近1/2，其粗糙度值越小，加工效果越好，由此判断仿真分析结果的准确性。在理想刀尖轨迹下二维振动铣削能够降低工件表面粗糙度，从而达到提高加工表面质量的效果。

4结语

本文对二维振动铣削过程中刀尖运动轨迹进行了分析，针对刀尖运动轨迹的特殊性，通过椭圆方程与旋转矩阵的结合，得出了一种计算二维振动铣削切削厚度的新方法。二维振动铣削是一种断续的切削形式，刀具与工件间歇性的接触有利于切削液的进入，这减小了刀具与工件间的摩擦，对抑制毛刺的产生和延长刀具寿命起到了很大的作用。获得理想螺旋状刀尖轨迹和切削厚度曲线的条件为：振动幅值与每齿进给量的比值应大于等于2，但其比值不宜过大，否则影响加工效率；同时振动频率与主轴回转频率的比值应近似于1/2。

参考文献：

[1]芮小健,张幼桢,钟秉林.振动切削过程的实质与机理研究[J].机械制造,1994(12):13-14.

RuiXiaojian,ZhangYouzhen,ZhongBinglin.EssenceandMechanismResearchofVibrationCutting[J].Machinery, 1994(12):13-14.

[2]ShamotoE,MoriwakiT.StudyonEllipticalVibrationCutting[J].AnnalsoftheCIRP,1994,43: 35-38.

[3]李启东,郭全英,张宏.微观动态切屑形成原理与分析[J].沈阳工业大学学报,2002,24(4):100-102.

LiQidong,GuoQuanying,ZhangHong.Micro-dynamicCuttingsFormingPrincipleandAnalysis[J].JournalofShenyangUniversityofTechnology, 2002,24(2):100-102.

[4]KimJD,ChoiIH.CharacteristicsofChipGenerationbyUltrasonicVibrationCuttingwithExtremelyLowCuttingVelocity[J].InternationalJournalofAdvancedManufacturingTechnology,1998,14(1):2-6.

[5]夏敬宇,朱训生,徐可伟,等.超声振动切削金属基复合材料的刀具磨损[J].航空精密制造技术,2002,38(2):1-4.

XiaJingyu,ZhuXunsheng,XuKewei,etal.UltrasonicVibrationCuttingMetallicMatrixCompositesCuttingToolWear[J].AviationPrecisionManufacturingTechnology, 2002,38(2):1-4.

[6]毛善峰,汤铭权，万迪慧.超声波振动切削时硬质合金刀具的磨损研究[J].东南大学学报,1995,25(3):50-54.

MaoShanfeng,TangMingquan,WanDihui.MechanismsofToolWearofCementedImsertsinUltrasonicVibrationCuttingProcess[J].Journalof

SoutheastUniversity,1995,25(3):50-54.

[7]MaC,ShamotoE,MoriwakiT.StudyontheThrustCuttingForceinEllipticalVibrationCutting[J].Mater.Sci.Forum.,2004,44(12): 396-400.

[8]AhnJH,LimHS,SonSM.ImprovementofMicroMachiningAccuracyby2DimensionalVibrationCutting[J].Proc.ASPE,1999,20:150-153.

[9]BrehlDE,DowTA.ReviewofVibration-assistedMachining[J].PrecisionEngineering,2008,32:153-172.

[10]高扬,顾立志.振动钻削理论与参数优化方法研究概况[J].工具技术,2008,42(10):27-30.

GaoYang,GuLizhi.ReserchSituationofVibrationDrillingTheoryandOptimizingParameterMethods[J].ToolEngineering, 2008,42(10):27-30.

[11]沈学会.超声振动辅助铣削加工技术及机理研究[D].济南：山东大学,2011.

[12]ChernGwoliang,ChangYuanchin.UsingTwo-dimensionalVibrationCuttingforMicro-milling[J].InternationalJournalofMachineTools&Manufacture,2006,46:659-666.

[13]丁辉. 二维振动辅助微细铣削机理及其实验研究[D].哈尔滨：哈尔滨工业大学,2011.

[14]TlustyJ,MacneilP.DynamicsofCuttingForcesinEndMilling[J].AnnalsoftheCIRP,1975, 24(1): 21-25.

[15]RasidiI.VibrationAssistedMachining:Modelling,Simulation,Optimization,ControlandApplications[D].London:BrunelUniversity,2010.

(编辑郭伟)