借助新技术上好实践课

齐雯逸

本节课是八（上）勾股定理第1节第2课时，在已探索得到勾股定理之后的内容，要求通过拼图验证勾股定理并体会其中数形结合的思想，会用面积法进行证明，体会勾股定理的应用价值并逐步培养学生应用数学解决实际问题的意识和能力，为后面的学习打下基础.学生在之前的《拼图与乘法公式》的学习中已经具备了一定的拼图活动经验，在以往的数学学习中已经经历了很多独立探究和合作学习的过程，具有了一定的自主探究和合作学习的经验，具备了一定的探究能力和合作与交流的能力.

在传统课堂中，学生学习的方式较为单一，掌握的证明方法也十分有限，对证明的过程、历史了解得不够详尽.为改变这种状况，笔者设计了一堂有关勾股定理证明的白板课，让学生通过pad来进行操作，目的是希望新的模式让学生更加主动地参与到整节课中，充分发挥他们的主观能动性.具体探究方案如下：

一、 学前先思，视频教学

课前用文件包给学生看微视频，里面对刘徽、梅文鼎的拼图法——出入相补法有所介绍.

（设计意图：结合曾经学过的《拼图与乘法公式》让学生更好地理解拼图法，体会数形结合思想.充分发挥pad的优势，在学前让学生自己进行思考，通过视频，可以形象生动地展现拼图过程，比一般纸质教学更加直观清晰.）

二、 复习设疑，激趣引入

（一） 利用考试系统，出示几道简单的习题，复习上节课内容，考查勾股定理的简单运用，学生在平板上作答后提交试卷，直接得到打分和答案.

（设计意图：充分发挥白板教学的优越性，了解学生对上节课知识的掌握情况.这与传统的练习不同，在实践过程中极大地提高了学生的兴趣.）

（二） 结合预习过程中的出入相补法，以抢答的方式到白板上进行操作，将印度婆什迦罗拼图通过拼接进行证明.

根据预习时观看的微视频中的方法，你能不能试一试，用下面这张图证明勾股定理？

（设计意图：检验学生的预习成果，是否真正掌握了拼图法.与传统教学不同，白板操作更加智能化、清晰化，每个学生用自己的pad更是可以体会到亲自动手操作的乐趣.）

（三） 引入本节课课题——验证勾股定理

三、 小组活动，拼图验证

如图，有四个全等的直角三角形（两直角边长分别是a、b，斜边长为c），请你将它们拼成一个能验证勾股定理的图形，并加以验证.可做适当标注.

学生将拼好的图从pad上投影到白板上，到白板上书写讲解.主要有以下几种证明方式：

（设计意图：让学生自己动手设计各种拼图，再用面积法来进行证明.加强学生对数形结合思想的认识，掌握拼图技巧，熟练地进行面积计算.通过这样的实践操作体会到数学与生活紧密相关，发现生活中的数学美.）

四、 追溯历史，激发情感

古今中外有无数的数学家对勾股定理进行了证明，动手搜一搜，看看你的想法与哪位数学大咖不谋而合.

学生将自己在pad上找到的材料公投到每个学生的pad上进行资源共享.

（设计意图：让学生自己通过网络搜索了解数学史，对自己刚刚通过拼图法验证的过程理解更加深刻.数学综合实践课不仅要培养学生的数学素养，更要培养学生对数学的兴趣.）

五、 课堂过关，能力提升

（一） 由主机统一发放试题给每一台pad，让学生当堂完成.

1. 一座建筑物发生了火灾，消防车到达现场后，发现最多只能靠近建筑物底端5米，消防车的云梯最大升长为13米，则云梯可以抵达该建筑物的最大高度是（      ）.

A. 12米 B. 13米

C. 14米 D. 15米

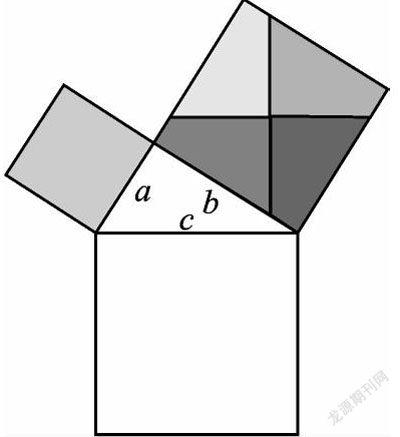
2. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长是7 cm，则正方形A、B、C、D的面积之和是_______cm2.

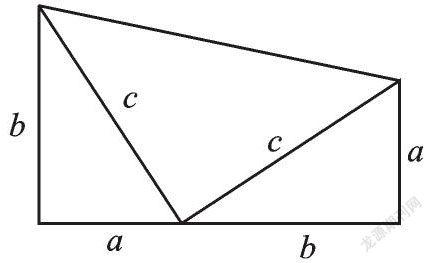
3. 美国第二十届总统加菲尔德也曾经给出了勾股定理的一种证明方法，如图，他用两个全等的直角三角形和一个等腰直角三角形拼出了一个直角梯形，请你利用此图形验证勾股定理.

（二） 学生提交试卷后当堂给出答案，由学生在pad上纠错，小组内讨论解决不会的问题，最后一题的讲解让学生到白板上进行讲解.

（设计意图：对于一堂数学综合实践课而言，保证教学效果仍然是十分重要的，因此需要一定的检测.通过整堂课的教学，要求学生能进一步用勾股定理解决问题，逐步加深对勾股定理的认识;最后一题通过对勾股定理的证明，面积法的应用得到再次强化，与数学史结合，提高学生对数学的兴趣，同时感受数形结合思想.）

六、 回顾反思，提炼升华

通过这节课的学习，你有什么样的收获？师生共同畅谈收获.（采取抽签的方式）

（设计意图：归纳出本节课的知识要点，数形结合的思想方法;教师了解学生对本节课的感受并进行总结;培养学生的归纳概括能力，希望学生对综合实践课有更新的认识.）

教师反思：整节课通过对勾股定理进行证明，让学生重新认识数学综合实践课，它不仅可以在传统课堂内进行，更可以打破常规、与时俱进，与新技术结合，让学生在玩中学.由于学生人手有一台平板电脑，所以在课前的预习也可以以新的形式展开，将需要呈现的形象化知识先让学生预习.在这里我选取了出入相补法，因为在传统纸质教材上，如果学生要学习这部分知识，相对会比较抽象，通过自己制作的微视频，将移动图形的过程呈现，学生很快就能学会这种方法，事实上在后来检测时也能感受到.拼图在历届考试中一直是比较热门的考点，以往的教学在拼图时学生只能自己动手剪纸操作，随着科技的进步，我们要好好利用新技术，学生能在pad上动手，积极性高涨，事实上教学效果也很不错.最后我不忘好好利用网络，让学生发现自己的证明居然和历史上的数学家不谋而合，他们的积极性和自信心都得到了提高.所以我们的综合实践课还是要创新，以各种各样的形式让学生体会到数学就在我们身边，数学之美是人人都可以发现的！

（作者单位：江苏省常州市武进区湖塘实验中学）