一窍通时百窍通

刘春花

课本例题是一类特殊的练习题，它承载着体现数学思想、揭示数学方法、规范思考过程的使命.那么如何将一道例题的作用发挥得“入木三分”呢？例题的变式与拓展就是一个有效方法.下面就以苏科版八年级上册第三章《勾股定理》中的一道例题为例，尝试对它进行变式与拓展，以帮助同学们达到学得“通”，用得“活”的目的.

一、 由“一棵树”想到“一片森林”

如图1，AD是△ABC的中线，AD=24，AB=26，BC=20，求AC.（课本第87页例2）

【分析】在△ABD中，已知AB、AD及BD的长可以判定△ABD为直角三角形，从而根据中垂线的定义可判断AD即为线段BC的中垂线，再由中垂线性质可得AC=AB.

【知识点】本题运用了勾股定理的逆定理，中垂线的定义及性质.—— 一棵树

【知识面】本题的目的是体会直角三角形与等腰三角形之间的密切联系，把研究等腰三角形转化为研究直角三角形.

——几棵树

【知识体】本题放入直角三角形中求线段的长.事实上初中阶段求线段长“放入”直角三角形是通法，不仅是勾股定理，还有三角函数.——一片森林

二、 由“一棵树”繁衍“几棵树”

变式一   如图2，在等腰△ABC中，AB=AC=26，BC=20，求BC边上的中线AD的长.

【变式依据】将原题中的一个已知与结论互换.

【变式目的】（1） 感受变中不变.虽然题目有变化，但解决问题的脉络不变.

（2） 加强知识点与知识面之间的联系.通过该题明晰“等腰三角形与直角三角形间的密切关联——高线”.

变式二   如图3，在△ABC中，AB=17，AC=10，BC=21，AD是BC边上的中线.求AD的长.

【分析】要求线段AD的长，可以将它“放入”一个直角三角形，利用勾股定理求得.那么是过A点还是D点构造直角三角形呢？若过D点构造，发现很难与已知条件建立联系，若过A点构造，则容易与已知产生关联，因此，先尝试过点A作AE⊥BC，构造直角三角形.

如图4，发现可在Rt△ABE和Rt△ACE中利用勾股定理建立方程，（设CE=x，则BE=21-x，在两个直角三角形中表示出AE2，得172-（21-x）2=102-x2，化简解得x=6），从而可求出线段AE、线段DE，最后再在Rt△ADE中利用勾股定理求出AD的长.

【变式依据】由特殊情况向一般情况转化.

【变式目的】（1） 感受勾股定理的强大，在直角三角形中已知任意两边可求第三边.

（2） 拓展思维，将特殊向一般转化;形成解题策略，构造直角三角形求线段长是常用方法.

这种方法不仅在勾股定理的应用上有价值，亦能影响后续三角函数的学习.

对于学习，我们有着美好的愿望——一通百通.正如吴承恩《西游记》：“这猴王也是他一窍通时百窍通，当时习了口诀，自习自练，将七十二般变化，都学成了.”若要想“百窍通”，那么就要先“一窍通”，若要“一窍通”，有效的方法是通过例题变式深入理解其精髓，掌握其数学思想方法，最终实现“活学活用”.

三、 自己“种树”，试一试，变一变

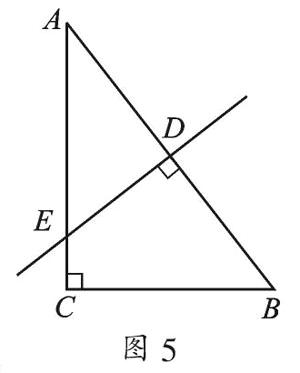
1. 如图5，在Rt△ABC中，∠C=90°，AC=12，BC=9，AB的垂直平分线分别交AB、AC于点D、E.求AE、EC的长.

【分析】首先连接BE，如图6，根据线段垂直平分线的性质，可得AE=BE，然后设AE=x，由勾股定理可得方程：x2=92+（12-x）2，继而求得答案.

解：连接BE，

∵AB的垂直平分线分别交AB、AC于点D、E，

∴AE=BE，设AE=x，则BE=x，EC=AC-AE=12-x，

∵Rt△ABC中，∠C=90°，AC=12，BC=9

【点评】此题考查了线段垂直平分线的性质以及勾股定理.此题难度不大，注意掌握数形结合思想与方程思想的应用.

2. 感悟分享

尝试精神：尝试能成功，成功能创新.前面的路，不论是一马平川还是千山万壑都要自己去走、去闯、去试，才使我们的生命更有意义.那么先从上一题的变式拓展开始尝试吧！

3. 我的变式分享

【悟空七十二变之一】

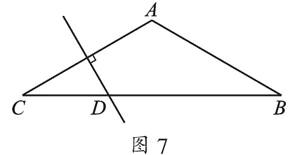
如图7，在△ABC中，AB=AC，∠A=120°，AC的垂直平分线交BC于D，若BC=12，求BD的长.

【答案】BD=8.

（作者单位：江苏省常州市武进区湖塘实验中学）