勾股定理中的分类讨论

潘美丽

在用勾股定理解决问题时，有些问题会出现多种情况，若分析不到位就会漏解或错解.这就需要我们利用分类思想对各种情况加以讨论，并逐类求解，然后综合得解.本文以一个中考题为例，对运用勾股定理解题时需要用到的分类思想加以探讨，供同学们参考.

【例题】（2010·黑龙江双鸭山）Rt△ABC中，∠BAC=90°，AB=AC=2. 以AC为一边，在△ABC外部作等腰直角三角形ACD，则线段BD的长为_______.

【分析】首先要结合题意，画出相应的图形.因为以AC为一边在△ABC外部作等腰直角三角形ACD，则AC可以是直角边，也可以是斜边，其中以AC为直角边又分两类，分别以A、C为直角顶点，所以有三种情况.

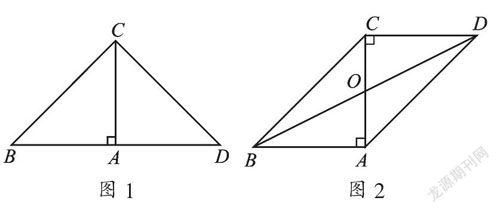
【解答】情况一：如图1，以A为直角顶点，向外作等腰直角△DAC，

∵∠DAC=90°，且AD=AC，

∴BD=BA+AD=2+2=4.

情况二：如图2，以C为直角顶点，向外作等腰直角△ACD，

∵△ACD是等腰三角形，

∴得AC=CD=2，

∠ACD=90°，

又∵∠BAC=90°，AB=AC=2，

∴AB∥CD且AB=CD.

∴四边形ABCD是平行四边形.

∴AC和BD互相平分，且相交于O，

情况三：如图3，以AC为斜边，D为直角顶点，向外作等腰直角△ADC，

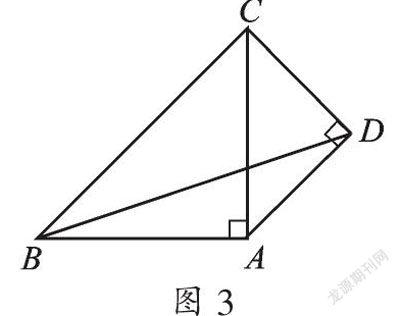
∵∠ADC=90°，AD=DC，且AC=2，

∴设AD=DC=x，

根据勾股定理，

建立方程x2+x2=22，

又∵△ABC、△ADC是等腰直角三角形，

∴∠ACB=∠ACD=45°，

∴∠BCD=90°，

又∵在Rt△ABC中，

【涉及知识点】等腰三角形，勾股定理.

【点评】本题中，符合条件的图形不唯一，所以结论存在多种情况.在应用一条已知线段构造等腰直角三角形时，这条已知线段可以是直角边，也可以是斜边.根据具体图形，结合勾股定理计算线段的长即可.本题主要考查勾股定理、等腰三角形性质的灵活运用，同时对分类讨论思想有较高要求.

同学们不妨尝试完成下列变式：

【变式】Rt△ABC中，∠BAC=90°，AB=AC=2.以BC为一边，在△ABC外部作等腰直角三角形BCD，则线段BD的长为_______.

【分析】本例同上例类似，都是有着与勾股定理有关的无图多解的特点.如果不注意分类讨论，就会漏解或错解.所以有必要利用分类讨论思想逐类求解.

参考答案：2或4或2.

同学们不妨再想一想，如何求AD的长？

【小练习】

1. 已知△ABC是等腰三角形，其中一边长是10，另一边长是8，则底边上的高为（      ）.

D. 以上都不是

2. 某园艺公司对一块直角三角形的花圃进行改造.测得两直角边长为6 m、8 m.现要将其扩建成等腰三角形，且扩充部分是以8 m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长.

【参考答案】

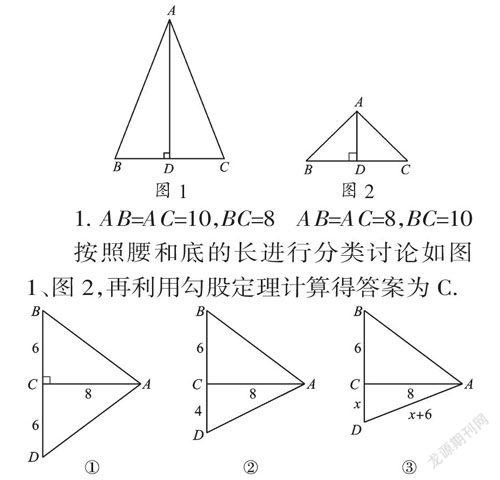
1. AB=AC=10，BC=8   AB=AC=8，BC=10

按照腰和底的长进行分类讨论如图1、图2，再利用勾股定理计算得答案为C.

2. 利用等腰三角形性质进行分类讨论，如图①②③，可利用勾股定理和方程思想求得答案分别为：32或20+4

【题型分析】此类题考查了运用勾股定理计算中的分类思想.要熟悉等腰三角形的分类，要全面分析在原来直角三角形的基础上可能构成等腰三角形的各种情况，防止以偏概全.题目如有图形则将变得很简单，按图形解答即可.但若没有图形，则需要讨论几种可能的情况，这正是“无图题前细思考，分类讨论保周到”.

总之，勾股定理作为解题中的一种工具，在中考中的应用十分广泛，覆盖了填空、选择、探究、证明等各种题型.它作为一种代数思想解决几何问题的最重要的工具，除了在等腰三角形中出现，更是常常与其他知识，如全等三角形、圆及图形变换等结合，同学们要能灵活运用所学知识，结合图形的特点，恰当分类解决问题.

（作者单位：江苏省常州市兰陵中学）