轻松玩“转”勾股定理
沈晓霞

转化是将未知的问题转化为已知的问题,把抽象的问题转化为具体的问题,把复杂的问题转化成简单的问题.勾股定理研究的是平面直角三角形中三边之间的关系,但在学习过程中时常会遇到立体图形上的问题,这时就要考虑到运用转化的思想,把立体图展开成平面图形,再利用平面几何的知识进行求解.

例1 如图1所示,有一根高为2 m的木柱,它的底面周长为0.3 m,为了营造喜庆的气氛,老师要求小明将一根彩带从柱底向柱顶均匀地缠绕7圈,一直缠到起点的正上方为止,问小明至少需要准备多长的一根彩带?
【分析】将一张直角三角形的纸片在铅笔上缠绕七圈,将纸片展开,发现彩带的长相当于直角三角形的斜边长(如图2),可以利用勾股定理求出彩带的长.

解:∵BC为木柱的高,
∴BC=2 m.
又∵木柱的底面周长为0.3 m,
∴AC的长为0.3×7=2.1(m).
在Rt△ACB中,由勾股定理,得AB2=AC2+BC2=22+2.12=8.41,=2.9.
因此彩带的长为AB=2.9 m.
【点评】遇到一些空间问题时,可通过动手实际操作一下,建立实物模型,这是建立空间概念的良好训练方法,而对实际问题进行分解、转化是数学解题中常用的思路.
例2 如图3,长方体的底面边长分别为2 cm和4 cm,高为5 cm,若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径是________cm.
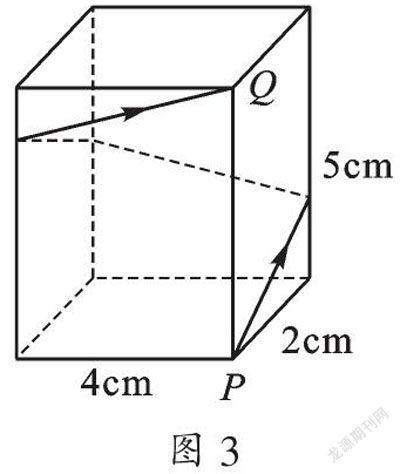
【分析】要求立体图形中的最短路径首先要化曲为直,即将长方体侧面展开成如图4所示,则PA=2+4+2+4=12(cm),两点之间线段最短,利用勾股定理便可解决.

解:PA=2+4+2+4=12(cm),
∵Rt△PAQ中,∠A=90°,
∴PQ2=PA2+AQ2,
∴PQ2=122+52=169,
∵PQ>0,∴PQ=13 cm.
【点评】很多数学新问题往往是通过形或数的逐步转化,化归为一个比较熟悉容易的问题,从而达到解决原问题的目的.
(作者单位:江苏省常州市武进区湖塘实验中学)

