万变不离其宗
蒋云红
学习数学,最重要的就是灵活运用,“变”才是数学的灵魂.看到“变”,很多同学会产生恐惧,其实我们只要熟练掌握核心概念、定理,抓住其形变而神不变之处,问题就能迎刃而解.下面我们以“勾股定理”这一章中的一道课本例题为例,对它进行一些变式探究.
原题 (苏教版教材八上第86页例1)《九章算术》中有一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意即:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子3尺远,问折断处离地面多高?
教材中有详细解答过程,此处不作赘述.

【变式1】一个三角形三边长的比是3∶4∶5,它的周长是60,求这个三角形的面积.
【思路点拨】一般我们看到比例,可设一份为k,则三边分别是3k、4k、5k,根据周长是60,得到k=5,从而三边分别是15、20、25,但要求三角形面积,本题还要用到勾股定理的逆定理.
解:设一份为k,则三边长分别是3k、4k、5k,有3k+4k+5k=60,∴k=5,
∴三边的长分别是15、20、25,
又∵152+202=625,252=625,
∴152+202=252,
∴ 它是直角三角形,斜边长为25.
∴它的面积是15×20=150.
答:这个三角形的面积是150.
【说明】变式1已知的是三边比例关系,若要求面积,一般三角形则必须求出一边及该边上的高,若特殊一点可运用勾股定理的逆定理说明这个三角形是直角三角形,问题也能迎刃而解.
【变式2】如图3,在直角梯形ABCD中,AD∥BC,AB⊥BC,以BD为折痕,将梯形ABCD折叠,使AD交BC于点E,点A落在点A1.
(1) 求证:BE=DE;
(2) 若AB=2,AD=3,BC=5,求△CDE的面积.

【思路点拨】
1. 图形中出现了角平分线(折叠出现了角相等)、平行线,容易得到等腰三角形;
2. 找到合适的直角三角形,巧用勾股定理,用方程思想求解.
解:(1) ∵折叠,∴∠ADB=∠BDA1,A1B=AB=2,A1D=AD=3,
∵AD∥BC,∴∠ADB=∠DBE,
∴∠BDA1=∠DBE,∴BE=DE.
(2) ∵折叠,
∴A1B=AB=2,A1D=AD=3,∠A=∠A1=90°.
在Rt△A1BE中,设BE=DE=x,则A1E=3-x,
根据勾股定理得,x2=(3-x)2+22,
【说明】折叠前后的两个图形是全等图形,对应边、对应角相等,另外还要注意多观察图形,找到合适的直角三角形,利用勾股定理列方程求边长.
【变式3】如图4所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5.求线段EF的长.
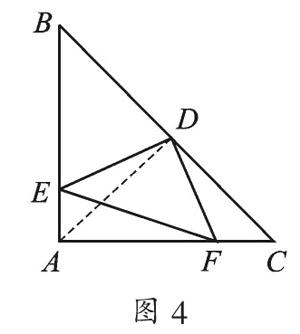
【思路点拨】现已知BE、CF,要求EF,但这三条线段不在同一三角形中,所以关键是线段的转化,考虑到三角形的中线有特殊的性质,不妨先连接AD.
解:连接AD.
∵∠BAC=90°,AB=AC,∴∠B=∠C=45°.
∵∠BAC=90°,AD为△ABC的中线,
∴AD=DC=DB.
∵AB=AC,AD为△ABC的中线,
∴AD⊥BC,∴∠BAD=∠B=∠C=45°.
∵∠EDA+∠ADF=90°,∠CDF+∠ADF=90°,∴∠EDA=∠CDF.
∴△AED≌△CFD(ASA),∴ AE=FC=5.
同理:AF=BE=12.
在Rt△AEF中,根据勾股定理得:
EF 2=AE 2+AF 2=52+122=132,∴EF=13.
【说明】通过此题,我们可以了解:当已知的线段和所求的线段不在同一三角形中时,应通过适当的转化把它们放在同一直角三角形中,再用勾股定理求解.
我们在练习过程中若能有意识地进行变式拓展训练,通过对例题、习题进行多角度、多层次的演变探究,使一道题变成一类题,一类题变成多类题,在不同角度、不同层次、不同背景下构建对勾股定理的认知,定能提高分析问题、解决问题的能力.
(作者单位:江苏省常州市翠竹中学)

