勾股定理史话

张伟俊

有人说，但凡伟大的发现背后都有一个美丽的传说.像勾股定理这样一个伟大的发现，又有什么传说呢？

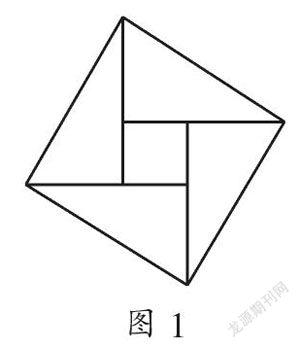
在我国，勾股定理又被称为商高定理.据西汉古算书《周髀算经》记载：周公问商高：“天不可阶而升，地不可得尽寸而度，请问数安从出？”意思是说：天的高度和地面的一些测量的数字是怎样得到的呢？商高说：“数之法出于圆方.圆出于方，方出于矩，矩出于九九八十一.故折矩以为勾广三，股修四，径隅五.既方其外，半之一矩，环而共盘，得成三、四、五，两矩共长二十有五，是谓积矩.故禹之所以治下者，此数之所生也.”即我们常说的勾三股四弦五.什么是“勾、股”呢？在中国古代，人们把弯曲成直角的手臂的上半部分称为“勾”，下半部分称为“股”.由此我国古代学者就把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.商高的意思是：当直角三角形的两条直角边分别为3（短边）和4（长边）时，径隅（弦）则为5.以后人们就简单地把这个事实说成“勾三股四弦五”.这是最早对于勾股定理的记载，但当时并未给予勾股定理的一般形式和证明.由于勾股定理的内容最早见于商高的话中，所以人们就把这个定理叫做“商高定理”.直到公元3世纪，我国汉代的数学家赵爽在注解《周髀算经》时，利用拼图的方法对勾股定理进行了证明，其证明用的拼图，被后人称为“赵爽弦图”. 2002年，国际数学家大会在我国北京举行，“赵爽弦图”被采纳为大会的会标（如图1），这是对我国古代数学辉煌成就的充分肯定.

在国外，对于勾股定理较普遍的称法是毕达哥拉斯定理.相传，在公元前5世纪，古希腊著名数学家毕达哥拉斯到朋友家作客，受朋友家地板图案的启发发现并证明了“直角三角形的两条直角边的平方和等于斜边的平方”.当时毕达哥拉斯从平淡无奇的方形地砖密铺的地板发现了“等腰直角三角形的两条直角边的平方和等于斜边的平方”的奥秘，继而思考一般的直角三角形是否也具有类似的性质.通过探究，毕达哥拉斯想出了一种非常简洁的证明方法：如图2，小直角三角形的两条直角边长分别为a、b，斜边长为c，拼成的两个大正方形面积相等，各去掉四个全等的直角三角形，剩余部分的面积相等，即可得到直角三角形的直角边长a、b和斜边长c满足a2+b2=c2，也就是“直角三角形的两条直角边的平方和等于斜边的平方”.这种证明方法在数学上还称之为“无字证明”呢！

据说，毕达哥拉斯在完成这一定理的证明之后欣喜若狂，杀牛百头以示庆贺.因此这一定理还获得了一个带有神秘色彩的称号——百牛定理.后来，古希腊的另一位数学家欧几里德（Euclid）在编著《几何原本》时，认为这个定理是毕达哥拉斯最早发现的，因而称之为“毕达哥拉斯定理”.为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票（如图3），图案由三个棋盘排列而成，显示的正是勾股定理的信息.

事实上，在很多国家都有关于勾股定理内容的记载.据了解，在现有的记载中，我国的记载是世界上最早的.我国著名数学家华罗庚，曾经提出这样一个想法：凡是有文明存在的地方，都应该会发现勾股定理.于是，他建议将反映勾股定理的图形（勾三股四弦五）发送到太空去，寻找是否有外星人的存在.

（作者单位：江苏省常州市武进区湖塘实验中学）