剖析错因 前车可鉴

陆军荣

初学勾股定理时，常易犯各种各样的错误.下面选择几例，供大家参考和反思，让同学们在今后的学习中不犯或少犯这类错误.

一、 思路僵化不变通

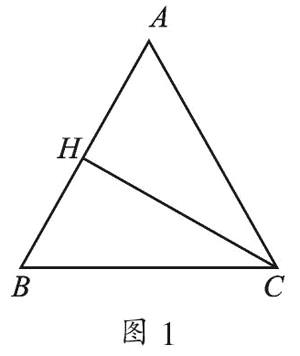
例1   等腰三角形ABC中，AB=AC=20，底边BC=24，求AB边上的高CH.

【错误解答】因为CH是三角形的高线，在Rt△ACH和Rt△BCH中，由勾股定理得：AC2-AH2=CH2，BC2-BH2=CH2，于是有202-AH2=CH2，242-BH2=CH2，到此无法得出CH的长.

【错误剖析】借助图形，在两个三角形中用勾股定理是正确的，但是最后为什么没有办法得出答案，是因为AH 和BH的长都不知道，未知量太多.既然有两个未知量，那么能否找到它们之间的关系呢？

【正确解答】方法一：设BH=x，那么AH=20-x，以CH2为桥梁，可得方程202-（20-x）2=CH2，

242-x2=CH2，

202-（20-x）2=242-x2，

x=14.4.

.

方法二：根据三角形的高线联想到三角形的面积，先作底边上的高，由勾股定理求出底边的高线长，得到三角形的面积，再根据等积法，求出CH的长度.

如图2，过A点作AD垂直BC于D点，

因为AB=AC，

所以BD=DC=12，

在Rt△ADC中，根据勾股定理得，

AC2=CD2+AD2，

202=122+AD2，

所以AD=16.

所以CH=19.2.

【点评】题目有多个未知量时，要准确设出未知数，根据它们之间的数量关系，表示出其他的量，然后根据题目中的等量关系列方程.需要开阔思路，灵活转化.

二、 漏用逆定理

例2   如图3，在C港有甲、乙两艘渔船，甲船沿北偏东60°方向以每小时8海里的速度航行，乙船沿南偏东以每小时15海里的速度航行，2小时后，甲船到M岛，乙船到P岛，两岛相距34海里，求乙船航行的方向.

【错误解答】由题意可知，甲船航行距离16海里，乙船航行距离30海里，根据勾股定理可以求出MP=34，所以△MCP是直角三角形，∠MCP=90°，得到乙船沿南偏东30°的方向航行.

【错误剖析】这道题的答案是正确的，但是解题过程是错误的，因为运用勾股定理的前提是直角三角形.对勾股定理概念理解不深刻，而忽视对三角形的形状进行判定.当题目没有指明直角三角形时，需要先根据三边的数量关系，运用勾股定理的逆定理判断三角形的形状.

【正确解答】由题意得：

CM=2×8=16（海里），

CP=2×15=30（海里），

∵在△CMP中，CM2=162=256，

CP2=302=900，PM2=342=1156，

∴PM2=CM2+CP2.

∴△CMP是直角三角形，∠MCP=90°，

180°-90°-60°=30°，

∴乙船沿南偏东30°的方向航行.

【点评】数学基础知识的学习包括概念学习、定理公式的学习以及解题学习三个方面.学习数学概念，要善于抓住它的本质属性，学习定理公式要抓住定理的内在联系、定理的适用范围及类型，学习数学解题的实质就是在熟练掌握概念与定理公式的基础上学会解决矛盾.

三、 割补不当

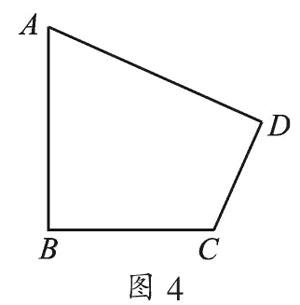
例3   如图4，已知在四边形ABCD中，∠B=∠D=90°，AB=2，CD=1.∠A∶∠C=1∶2，求BC和AD的长.

【错误解答】分析题意找到∠B=∠D=90°，联想到勾股定理，连接AC，分别使用勾股定理，发现应用勾股定理缺少一条边，并且，条件中两个角的比值无法使用，至此无法解决这个问题，陷入死胡同.

【错误剖析】根据两个直角把四边形用割的方法分成两个直角三角形，但是不能充分运用条件∠A∶∠C=1∶2，所以分割不恰当，那怎么办呢？不妨用“补”的方法.

【正确解答】根据四边形的内角和公式和∠A∶∠C=1∶2，我们可以得出∠A=60°，∠C=120°，要用特殊角就要放入三角形中，从而想到延长AD，BC交于点M，如图5，分别使用“直角三角形中，30°角所对的边是斜边的一半”，用两个直角三角形边的关系求出BC、AD的长.

【点评】割补法相当于我们的加减法，要灵活运用，不要生搬硬套，才能巧妙解题.

四、 思维定势致漏解

例4   已知在△ABC中，AB>AC，AD是中线，AE是高.求证：AB2-AC2=2BC·DE.

【错误解答】如图6，AE是三角形的高线，由此想到存在三个直角三角形，利用勾股定理表示出两边的平方，再用平方差公式就可以得到结论.

【错误剖析】由于题设中没明确指出△ABC的形状，也没给出图形，因此，这个三角形有可能是锐角三角形、直角三角形或钝角三角形.所以高线AE既可以在三角形内（如图6），也可以在三角形外（如图7），还可以与一边重合（如图8）.这三种情况都要考虑.而这里只证明了其中的一种情况，思维定势作祟.

【点评】数学思维有习惯性，但是我们的思维不能固定不变，善于变化也是数学思维的特征.正确的思维定式是“先阶段，后综合;勤总结，多温故”.

（作者单位：江苏省常州市兰陵中学）